canvas进阶：贝塞尔曲线推导与物体轨迹运动实现

"这篇教程主要探讨了canvas中的贝塞尔曲线公式推导以及如何实现物体跟随曲线轨迹运动。文章首先介绍了贝塞尔曲线的概念，并通过一、二阶贝塞尔曲线的推导帮助读者理解变量t的含义。同时，给出了一个示例，展示了一个小球如何沿着由贝塞尔曲线生成的轨迹移动。" 在计算机图形学中，贝塞尔曲线是一种用于创建平滑曲线的数学工具，广泛应用于2D和3D图形渲染，特别是在canvas这样的绘图环境中。一阶贝塞尔曲线由两个点（起点P0和终点P1）定义，而二阶贝塞尔曲线则增加了两个控制点（Pa和Pb），使得曲线更加灵活且能够更好地模拟真实世界物体的运动轨迹。 贝塞尔曲线的推导关键在于理解变量t，它代表了曲线从起点到终点的参数进度，其取值范围在0到1之间。在一阶贝塞尔曲线中，t可以理解为从P0到P1线上某点Pt的比例，即P0pt/ptp1=t。随着时间的推移（可以理解为速度v乘以时间），物体沿曲线移动，t的值会从0逐渐增加到1，表示物体完成了整个运动过程。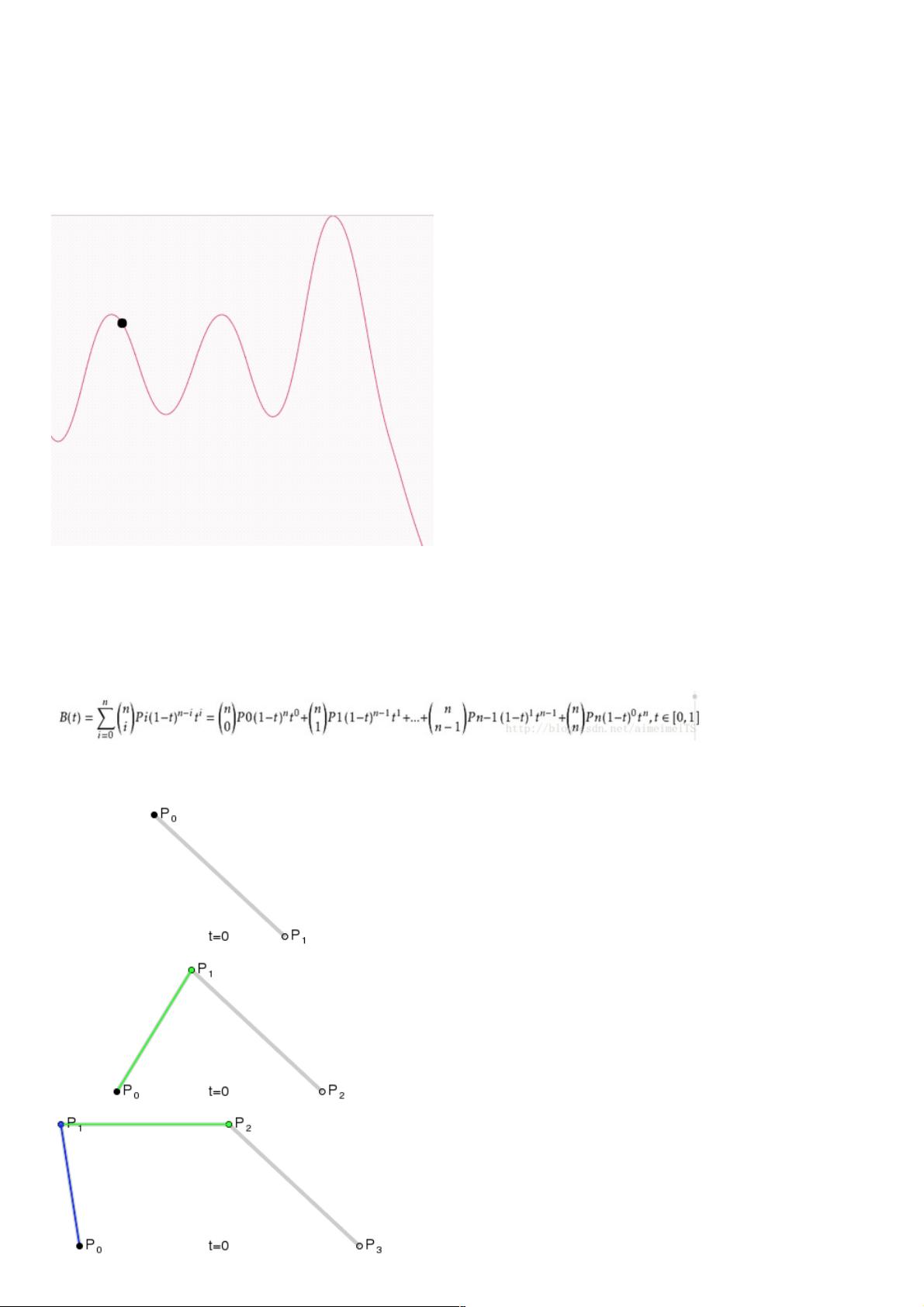 二阶贝塞尔曲线的推导则是通过将Pa和Pb的连线看作是一条一阶曲线，然后将两端的一阶曲线结合，形成一个更复杂的曲线。这样，每个控制点Pa和Pb又可以视为新的起点和终点，通过再次应用一阶贝塞尔公式，最终得到二阶贝塞尔曲线的表达式。以此类推，可以构建更高阶的贝塞尔曲线。 物体跟随贝塞尔曲线轨迹运动的实现，通常涉及到定时器和动画帧的更新。每帧中，物体的位置根据当前的t值计算，随着t的增加，物体沿着曲线平滑移动。在canvas中，可以使用`requestAnimationFrame`函数来实现这一过程，不断更新物体的位置并重绘场景，从而模拟出物体沿曲线运动的效果。 总结来说，这个教程深入浅出地讲解了贝塞尔曲线的基本概念、推导过程以及在canvas中应用的实例，对于想要提升canvas技能或者理解图形学中曲线运动原理的开发者来说，是非常有价值的参考资料。通过学习，开发者不仅可以掌握贝塞尔曲线的理论知识，还能动手实现物体跟随复杂曲线轨迹的动画效果。