理解时间序列预测：基础概念与Python实现

"本文主要探讨时间序列预测的基本概念，包括平稳序列的重要性，以及如何通过Python中的库进行相关分析。文章以实例为基础，介绍了创建时间序列预测的步骤，并使用了statsmodels、numpy、pandas等Python库。" 在时间序列预测中，我们关注的是随时间变化的数据集，这些数据往往展现出重复的模式，例如季节性变化、周期性波动等。这样的数据广泛存在于天气、交通流量、生理信号、金融市场和销售等领域。分析这些序列有助于识别规律并预测未来的趋势。 首先，要进行时间序列预测，关键一步是理解平稳序列的概念。平稳序列是指其统计特性，如均值、方差和自相关性，随着时间保持相对稳定。这使得预测变得更为简单，因为这些特性不随时间的推移而显著改变。相反，非平稳序列的统计特性会随时间变化，增加了预测的复杂性。 1.1 常数均值 在平稳序列中，均值是一个固定不变的数值，序列围绕这个均值上下波动。如果序列的均值随着时间逐渐增加或减少，那么序列就不是平稳的。示例代码创建了一个随机数序列，展示了如何计算每个时间点的滚动平均值来观察均值的变化趋势。 为了验证序列的平稳性，通常需要进行统计测试，如ADF（Augmented Dickey-Fuller）检验，用于检测序列是否存在单位根，即判断序列是否为非平稳。此外，还可以通过可视化手段，如ACF（自相关函数）和PACF（偏自相关函数）图，来直观地检查序列的自相关性。 1.2 常数方差 平稳序列的另一个重要特性是方差的恒定。如果方差随时间变化，意味着数据的波动程度在增加或减少，这可能表明序列是非平稳的。保持恒定的方差有助于预测未来的波动幅度。 1.3 自相关 自相关是指序列当前值与其过去值之间的关联性。在平稳序列中，自相关通常会随着滞后值的增加而快速衰减。通过ACF图，我们可以观察到这一现象，如果自相关系数在一定滞后后接近零，说明序列可能是平稳的。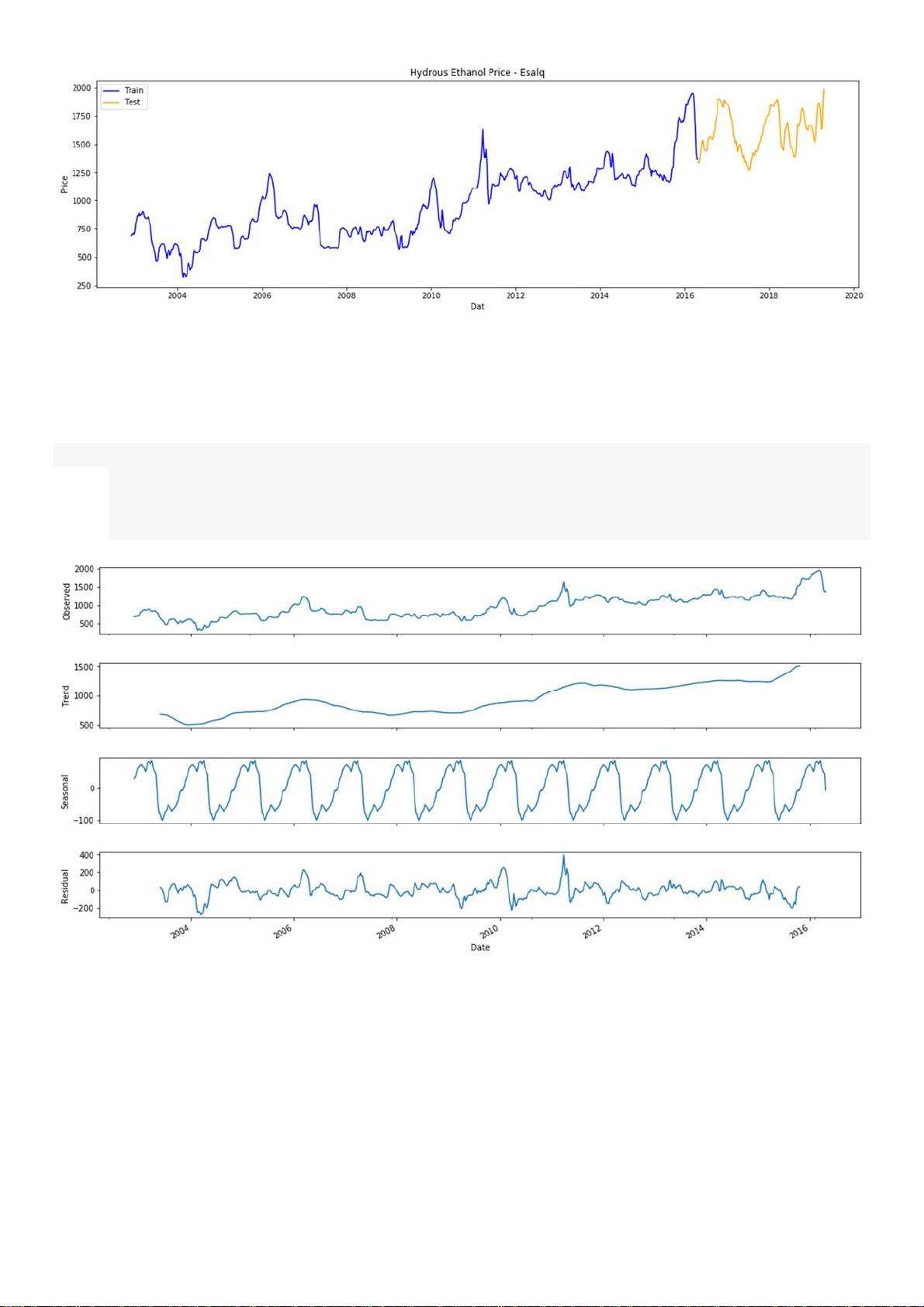 在Python中，可以使用statsmodels库的`plot_acf`和`plot_pacf`函数来绘制ACF和PACF图，以辅助判断序列的平稳性。另外，`seasonal_decompose`函数可用于分析数据中的季节性成分，这对于理解和预测周期性时间序列至关重要。 在进行时间序列预测时，往往需要对非平稳序列进行预处理，如差分、对数变换等，使其转化为平稳序列，然后再应用ARIMA（自回归积分滑动平均模型）、季节性ARIMA（SARIMA）或其他预测模型。 时间序列预测的核心是理解并处理数据的平稳性，通过Python中的统计工具和库，我们可以有效地分析数据、识别模式，并构建准确的预测模型。这篇文章通过实例和代码演示了如何在实践中应用这些概念。