MATLAB实现的Mallat算法实验：离散小波变换与图像处理

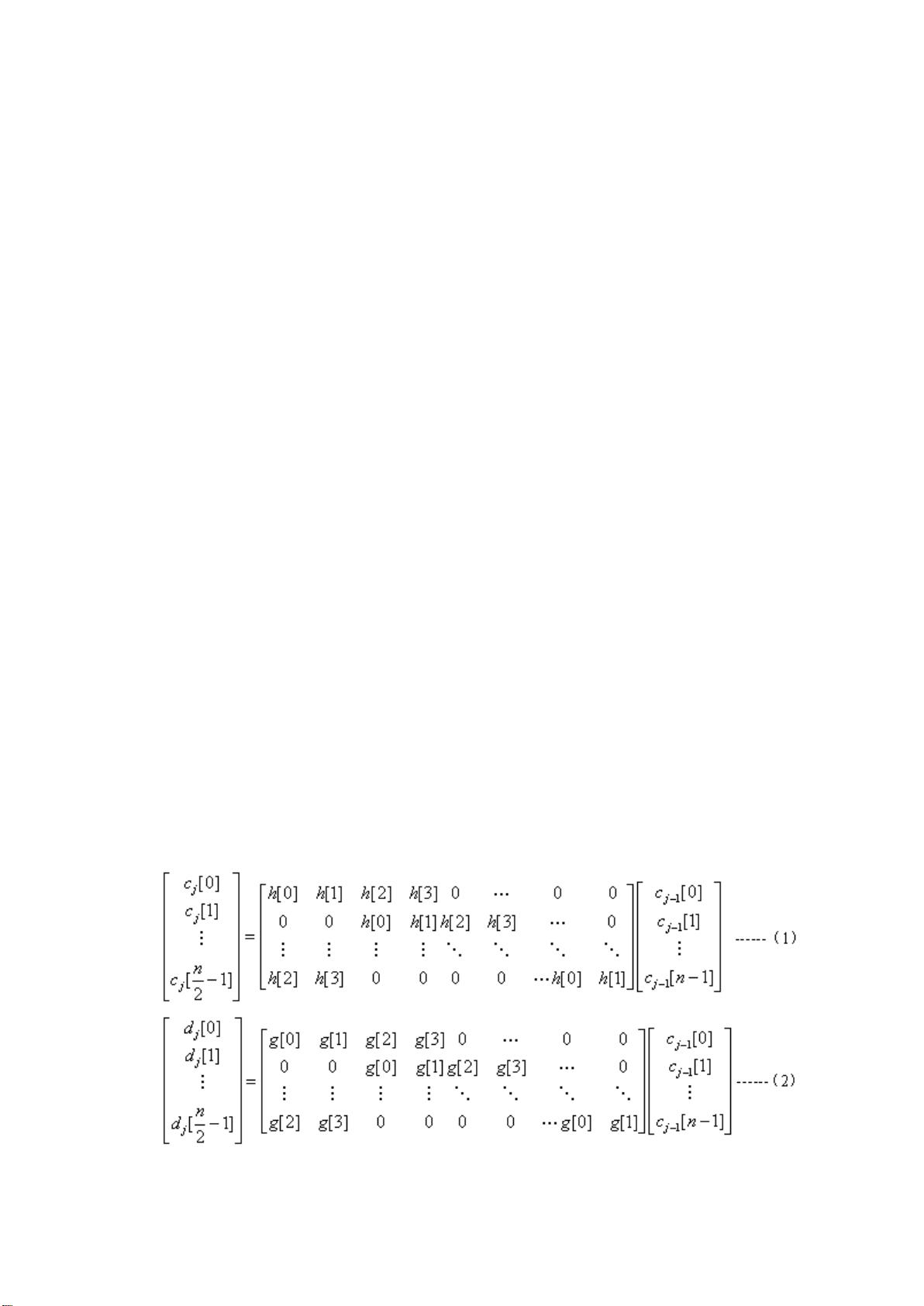
Mallat算法是一种基于小波变换的信号处理方法，主要用于离散信号的分析和重构。实验报告通过实际操作对Mallat算法进行了详细的阐述，以二维离散小波变换为例。实验的核心内容包括以下几个步骤： 1. **实验内容**： - 选取图像（如蕾娜图像）作为输入，进行二维离散小波变换，选择变换级数超过三级。 - 应用阈值化处理，例如设置阈值约为10，目的是降低噪声和提取有用的信息。 - 统计系数中0的个数，这是判断信号细节的重要指标，有助于保留关键特征。 - 重构图像，并计算重构后的图像的方差和峰值信噪比（PSNR），以评估重构质量和信号的完整性。 - 生成小波能量的三维视图，以便观察不同尺度下的能量分布，理解信号的不同频率成分。 2. **实验原理与编程思路**： - Mallat算法采用递归的方式进行小波分解，每次通过低通和高通滤波器分离出高频和低频成分，形成尺度上的子带。 - 分解和重构算法利用卷积操作，通过矩阵形式表示，如使用快速傅里叶变换加速卷积计算。 - 在分解过程中，进行两次下采样，减少点数但保持总能量不变。重构则涉及插零、滤波器应用及重新组合系数。 3. **具体流程**： - 实现了两个主要函数：mdec1（一级小波分解）和mrec1（一级小波重构），用于处理单次分解和重建。 - 对于多级小波分解和重构，可能涉及到递归调用这些函数，逐级处理信号的细节和粗粒度信息。 4. **性能评估**： - 峰值信噪比（PSNR）是衡量重构图像质量的重要指标，它反映了原始信号与重构信号之间的差异，数值越高，表示重构质量越好。 通过这个实验，学习者不仅能掌握Mallat算法的理论基础，还能提升编程技能，特别是矩阵运算和快速算法的应用，以及信号处理的实际操作。此外，对于图像处理、信号分析等领域有着重要的实践价值。