从4G到6G：波束空间复用的实践、理论与趋势

需积分: 3 131 浏览量更新于2024-08-04 收藏 1.75MB PDF 举报

"这篇文章深入探讨了'Beam-space Multiplexing'的概念，从4G TD-LTE、5G到6G及其未来的发展趋势。作者包括Shanzhi Chen、Shaohui Sun、Guixian Xu、Xin Su和Yuemin Cai，他们都是该领域的专家。文章提出了新的术语'beam-space multiplexing'来描述4G TD-LTE在3GPP发布中的多层波束形成技术，并对这一技术进行了系统性的工程和理论分析。" 正文： "在无线通信领域，Beam-space Multiplexing（波束空间复用）是一种提高频谱效率和传输容量的关键技术。这一概念的提出，旨在解决传统多层波束形成技术在理论分析、信道状态信息获取以及工程实施方面的局限性。文章首先明确了beam-space multiplexing的基本理论，通过对比与 antenna-space multiplexing（天线空间复用）的不同，阐述了其在空间维度上利用更高效的方法。文章详细总结了4G TD-LTE和5G新无线电（NR）中beam-space multiplexing的关键技术及其3GPP标准化进程。在4G TD-LTE阶段，它体现在多层波束形成，而在5G阶段，则更多地与大规模波束形成相结合。这两种方式都旨在提升无线通信系统的性能。系统级性能评估是理解beam-space multiplexing效果的重要手段。文章提供了这种复用方案的性能评估结果，这些结果来自于现有的商业TD-LTE网络以及5G的实地试验。实际部署的案例，如4G TD-LTE和5G蜂窝网络的运营，为这一技术的应用提供了实证依据。此外，文章还探讨了未来6G及以后的发展趋势，beam-space multiplexing将如何适应更高的数据速率需求、更低的延迟挑战，以及更复杂的网络环境。随着无线通信技术的持续演进，beam-space multiplexing有望在提高系统容量、增强覆盖范围以及优化用户体验方面发挥更大的作用。这篇综述文章为读者提供了一个全面而深入的视角，来理解beam-space multiplexing的实践、理论及其未来的发展。对于研究人员和工程师来说，这是一份宝贵的参考资料，有助于他们在设计和优化无线通信系统时更好地利用波束空间复用技术。"

Then, we ﬁrst review the multiplexing capacity of deter-

ministic MIMO channels with antenna-space multiplexing. For

antenna-space multiplexing, the capacity for single user with

time-invariant channel is

min

i=1

log



1 +

∗



bits/s/Hz,

where n

min

:= min(N

, N

) and µ

is the i-th singular

value (descending order) of channel H that represents the

spatial channel with N

transmit antennas and N

receive

antennas; N

denotes the noise power at the receiver and

∗

, . . . , p

∗

are the allocated power for spatial parallel sub-

channels determined by water-ﬁlling [8]. At high SNR, equal

power allocation policy is the asymptotically optimal, the

capacity can be derived by

ant−space

≈

i=1

log



1 +

total



(1)

≈ k log

(SNR) +

i=1

log





bits/s/Hz.

where SNR = P

total

and k also denotes the number of

spatial degrees of freedom offered by multiple antennas.

With beam-space multiplexing, the received signal vector

at the receiver can be expressed as y = HVs + n, where

V ∈ C

×r

is the optimal beamforming matrix with r beams

such that the spatial multiplexing shifts to beam domain from

antenna domain, and n is the additive noise at the receiver.

When r = 1, it is traditional beamforming. Then, the capacity

is C

beam

= log

(1 + SNR µ

) such that high power efﬁciency

is gained. Assuming the effective channel HV has r non-zero

singular values, and r ≤ k. Similarly, the achievable capacity

can be written as

beam−space

≈ r log

(SNR) +

i=1

log





bits/s/Hz. (2)

As a result, we can see that the receive SNR can be improved

without extra power consumption while multiplexing gain

could also be achieved by beam-space multiplexing.

B. Comparison of CSI Acquisition Between TDD and FDD

In order to align beam to each spatial data piece of beam-

space multiplexing accurately, CSI should be acquired at

the BS before the transmission. In FDD systems, CSI can

be obtained through reference signal training and quantized

feedback. However, the performance is limited by several non-

ideal factors, such as feedback delay, quantization error, and

imperfect CSI estimation at user side. This will lead to the

engineering implementation challenge due to heavy overhead

of real-time feedback. The limitation becomes extremely se-

vere in 5G, where the number of antennas in the BS is large

and the reference signal symbols are limited. The required

independent reference signal symbols are proportional to the

number of antennas at the BS. The number of available

reference signal symbols is fundamentally limited by the

channel coherence time. Thus, the reference signal symbols

will become insufﬁcient for accurate channel estimation in

FDD systems with large number of antennas at the BS.

Recently, compressed sensing (CS)-based channel estima-

tion methods have been proposed to reduce the reference signal

overhead for FDD massive MIMO systems, e.g., orthogonal

matching pursuit (OMP) and least absolute shrinkage and

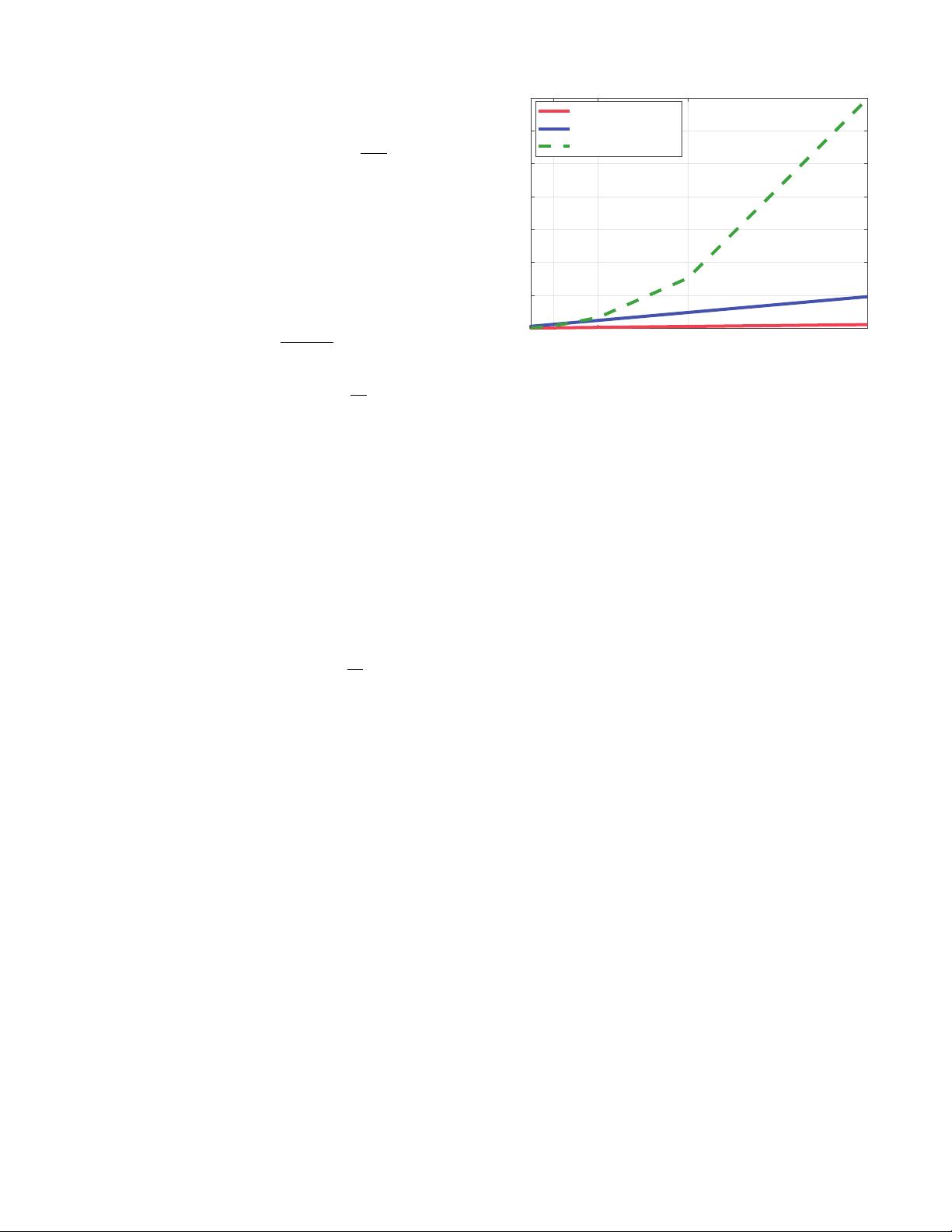
16 32 64 128 256

Number of transmit antennas at BS

Gflops

TDD with 10 UEs

TDD with 50 UEs

FDD

Fig. 2: Computational complexity of CSI estimation for TDD

and FDD systems.

selection operator (LASSO) algorithm [9]. It has shown

that the massive MIMO channel usually exhibits abundant

sparsity in certain transformed domains due to limited local

scatters in physical environments. However, there are some

drawbacks for the CS-based algorithms. For example, group

sparsity and other sparse structure in the different domains

are not well exploited. This is because of the limitation of

the solution for the CS optimization problem. To overcome

this problem, a structured compressing sensing (SCS)-based

spatio-temporal joint channel estimation scheme is proposed

to reduce the required pilot overhead, whereby the spatio-

temporal common sparsity of delay-domain MIMO channels

is leveraged. Moreover, the design of non-orthogonal pilot

for CS-based adaptive CSI acquisition for improving channel

estimation performance.

Alternatively, in TDD systems, channel reciprocity property

can be utilized for CSI acquisition. The pilot overhead for CSI

estimation in TDD massive MIMO systems is only propor-

tional to the number of users. Furthermore, as shown in Fig. 2,

in contrast to FDD systems, the computational complexity for

CSI estimation in TDD system is relatively much lower [10].

However, strictly synchronization and antenna calibration are

required to guarantee the channel reciprocity. This is because

reciprocity holds only in air channel between the BS and

user side. If the transceiver of BS and users are considered,

downlink and uplink channels are no longer reciprocal. Thus,

in practice, calibration is needed to restore channel reciprocity.

Recently, user-assisted calibration is an enabling technology

for TDD massive MIMO in 5G, which yields fast calibration

processing with low overhead and high calibration accuracy.

It is expected that more efﬁcient calibration algorithms can be

emerged such that the multi-fold gain of massive MIMO in

TDD network can be fully realized.

C. Comparison of Engineering Implementation

We compare the beam-space multiplexing with the tradi-

tional antenna-space multiplexing by considering the prac-

tical engineering implementation constraints. For practical

implementation with antenna-space spatial multiplexing, large-

spaced (i.e., 4 ∼ 10λ) two and four antennas were used

to provide enough decorrelation of multiple antenna signals,

剩余10页未读，继续阅读

digit123

粉丝: 1
资源: 32

从4G到6G：波束空间复用的实践、理论与趋势

20 LTE-from theory to practice

4G移动通信技术权威指南：LTE与LTE-Advanced.4G LTE.LTE-Advanced for Mobile Broadband

irs-aided-swipt-joint-waveform-active-and-passive-beamforming-design:本文研究了一种高效的IRS辅助SWIPT架构，其中多载波多天线AP在IRS的帮助下同时向单天线用户传输信息和功率

写一个digital sub-carrier multiplexing system的简单的matlab代码

ffmpeg用一条命令依次推流多个264文件到rtsp

音频驱动中TDM和I2S有什么区别

mimo和mu-mimo技术的区别

flume扇出流的形式

IO 多路复用是什么意思？详细从底层原理及实现解释一下，不少于3000字

光通信 用英文怎么说

最新资源

光通信用英文怎么说