COMSOL 5.4: 导磁球在静磁场中的分析

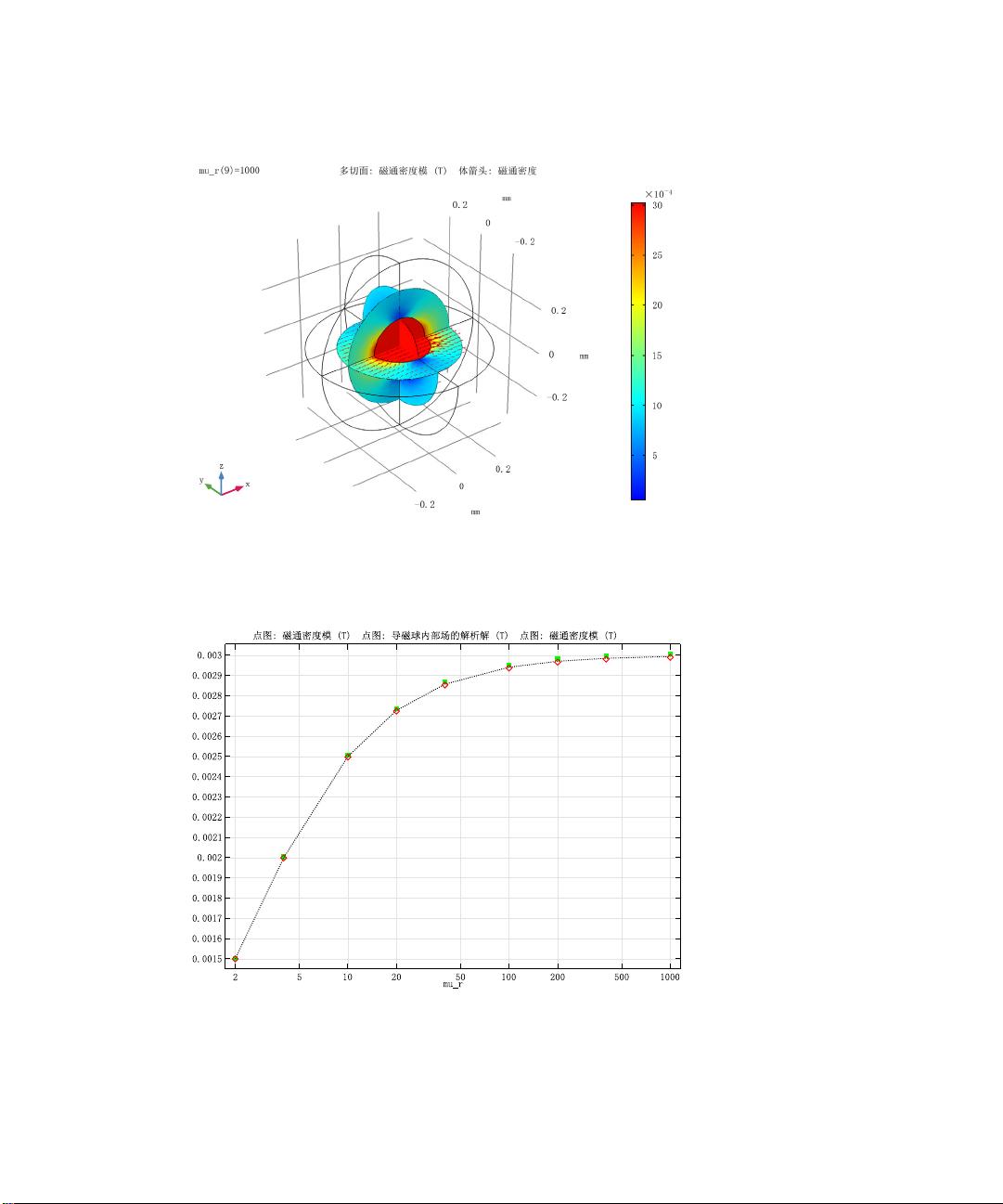
"COMSOL Multiphysics 5.4 静磁场中的导磁球模型展示了如何解决相对磁导率大于1的球体在均匀静态背景磁场中的问题。模型通过两种不同的公式进行求解，并比较了解析解和计算解的差异。" 在COMSOL Multiphysics 5.4中，该模型涉及了电磁学的一个核心概念——静磁场。模型的核心是一个相对磁导率（μr）大于1的导磁球，它被置于1mT的均匀背景磁场中。磁导率是材料对磁场的响应度量，μr大于1意味着该材料比空气（通常μr≈1）更易磁化。 模型的构建包括三个同心球体：导磁球本身、一个表示自由空间的中间球壳体积，以及一个模拟无限延伸区域的外部壳体积，后者利用“无限元域”特性来处理边界条件，确保外部边界不影响解。当球体在背景磁场中时，会产生内部磁场，其解析解可由公式给出： \[ B = \frac{3\mu_r B_0}{\mu_r + 2} \] 其中，\( B_0 \) 是背景磁场的强度。 问题的求解采用了两种方法。第一种方法是通过“磁场，无电流”接口，使用标量势公式，即基于磁通量守恒的偏微分方程来求解磁标势场 \( V_m \)。背景磁场 \( H_b \) 指定后，可以计算出 \( H \) 场，进而得到 \( B \) 场。由于控制方程涉及标量势的梯度，采用拉格朗日单元公式，需要在模型中某一点约束磁标势的值以确定常数。 第二种方法是使用“磁场”接口的矢量势公式，直接根据 \( A \) 场来指定背景场和边界条件，计算 \( B \) 场的旋度。这种方法使用旋度单元公式，不需要像标量势公式那样精细的网格也能获得高精度。 模型的结果以图2和图3展示，分别对应两种方法计算的磁场分布，均在μr=1000的情况下。无限元区域的磁场未绘制，因为它没有物理意义。图4对比了两种方法下磁场的增强情况，揭示了解析解和数值解的相似性和可能存在的差异。 通过这个模型，用户可以深入了解不同求解方法对结果的影响，以及在处理导磁材料时如何精确地模拟磁场分布。这对于电磁设备设计、磁性材料研究等领域具有实际应用价值。