R.M. Rizk-Allah
/
Journal of Computational Design and Engineering 5
(
2018
)
249
F
5
¼
1
P
15
mmx
4
-16x
2
-5x
i
mm
15 ½-10;10] -78.332314
2.2.
文献综述
在文献中,许多元启发式算法(MHA)已被提出来解决EDP。
Liu,Wu,Wu,and Wang(2015)的作者提出了一种差分搜索算法
来求解结构EDP,其中通过使用动态S型软阈值惩罚机制来处理约束。
在(Liu,Teo,Wang,Wu,2016)中,基于精确罚函数法的思想引
入 了 一 种 差 分 搜 索 算 法 , 用 于 解 决 约 束 优 化 问 题 。 在 ( Canayaz
Karci , 2016 ) 中 , 引 入 了 一 种 板 球 算 法 Cuevas 等 人 Cuevas 和
Cienfuegos(2014)开发了用于处理约束问题的社交蜘蛛优化(SSO-
C) 。Coello(2000),Deb( 1991,2000,1997),Dimopoulos
(2007)中的作者介绍了GA,
He and Wang(2007),He,Prempain,and Wu(2004),
Cagnina,
2.3.
正弦余弦算法
SCA
是一种基于种群的优化算法,它是基于数学正弦和余弦函数
建立的与其他
MHA
类似,
SCA
通过随机创建一组解决方案来启动搜
索过程然后,通过使用目标函数来评估这些解决方案。然后,算法存
储到目前为止获得的更好的解决方案,将其表示为目的地点,并且根
据正弦和余弦函数更新解决方案以创建新的解决方案(参见等式
10
)。(
3
))。最后,当满足最大迭代次数时,算法停止优化过程
8
>
x
j
;
t
r
1
×si
n
r
2
×
j
r
3
P
j
;
t
-
x
j
;
t
j
r
4
0
:
5
Esquivel和Coello(2008)提出了PSO算法来解决
的EDPs。In(Fesanghary,Mahdavi,Minary-Jolandan,
Alizadeh,
Mahdavi,Fesanghary,Damangir,2007)harmony search
算法应用于这些问题。Garg(2014)使用人工蜂群算法,而杜鹃搜索
算 法 ( Yang Deb , 2010 ) 用 于 求 解 EDP 。 Hwang 和 He
(Hwang&He,2006)提出了一种混合算法,称为模拟退火遗传算法
来求解EDP。在(Kaveh Talatahari,2010)中,提出了一种通过应
用 有 限 元 方 法 来 求 解 EDP 的 改 进 蚁 群 优 化 算 法 , 而 在 Kaveh 和
Talatahari(2009)中,提出了一种基于被动聚集粒子群优化、蚁群优
化和和声搜 索 的 混合 算 法来 求 解EDP。在 (Hedar&Fukushima,
2006)中,提出了一种滤波模拟退火(FSA)算法来处理约束问题。
Liu等人Liu, Cai,and Wang(2010)提出了一种基于粒子群优化
PSO和差分进化(DE)的集成算法,并将该混合算法用于求解EDP。
此外,有助于优化应用的更多研究工作可以在文献中找到(Wang等
人,2016; Zhang,Zhou,Jin,Wang,&Cicloviki,2014; Zhang等
人,2013,2016; Zhang等人,2017; Zhou,Zhao,Zhang,Adali,
&Cicloviki,2016)。
j1; 2;.. . ; n
其中n是维数,x
j
;
t
是当前解在
第
t
次
迭代时第
j
维中的位置,P
j
(目的地)是
第j次迭代时到目前为止最佳解的位置。
维数,
r1
;
r2
;
r3
;
r4
是随机数,并且:表示绝对值。 搜索代理的解决方案表
示为
x
i
¼x
i
;
1
; x
i
;
2
;.. . ; x
i
;
n
n n n; i 1; 2;.. . PS,PS是搜索代理的人口规模。
如图所示,
Eq
。(
3
)
SCA
包含四个参数。第一个参数是
r
1
,它
表示候选区域,无论是目标和候选解决方案之间的区域还是从候选解
决方案延伸的区域。第二个参数是
r
2
,它规定了向目的地或向目的地
外移动的距离第三个参数是
r3
,它随机分配目的地的权重,其中它负
责强调(
r3
>
1
)或不强调(
r3
1
)
<
目的地在确定距离。最后,参数
r4
负责在方程中的正弦项和余弦项之间切换(三)、此外,自适应地调
整参数
r1
,以
表2
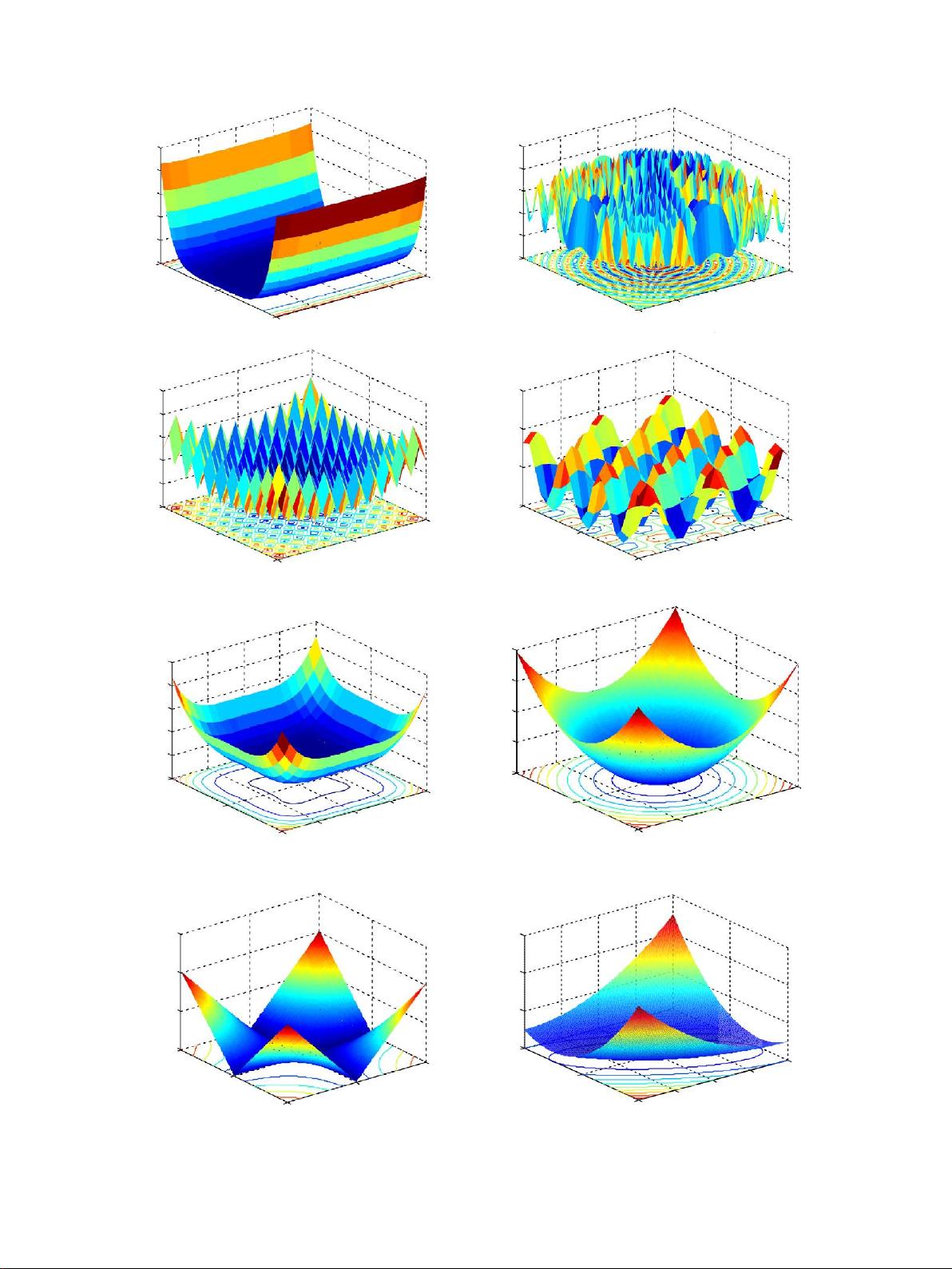
基准功能。
好玩的
n
范围最佳
x
4
x
2
双甲氧基硅烷
-
4双
甲氧基硅烷
2
双甲氧基
硅烷
2
½-20;20]
-1.0316284
F
3
¼
P
3
10x
2
-10cosmetic 2
p
x
i
cosmetic10x3
½-5;5] 0
f
9
½
max
i
fj
x
i
j ;
1
6
i
6
n
g
30
½-100;100]
0
30
½-
100
;
100
x
4
随机
1
/2
0
;
1
/
30
1/2 -
1
:
28
;
1
:
28
]
-x
i
sinjx
i
j
30 ½-500;500] -418.9829 5
12
x
2
-
10
co
s
2
p
x
i
10
]
30
12
-
5
:
12
;
5
:
12
]
0
F
15
¼
-
20ex
p-
0
:
2
q
1
P
n
x
2
-
exp
.
1
个
P
n
cosmetic 2
p
x
i
cosmetic
20xe
30
½-32;32]
0
F
17
¼
p
f
10
si
n
p
y
i
P
n
-
1
y
i
-
1
2
½
1
10
sin
2
p
y
i
1
]
p
y
n
-
1
2
g
P
n
ux
i
;5; 100;400
30 ½-50;50] 0