理解SVM：支持向量机详解与应用

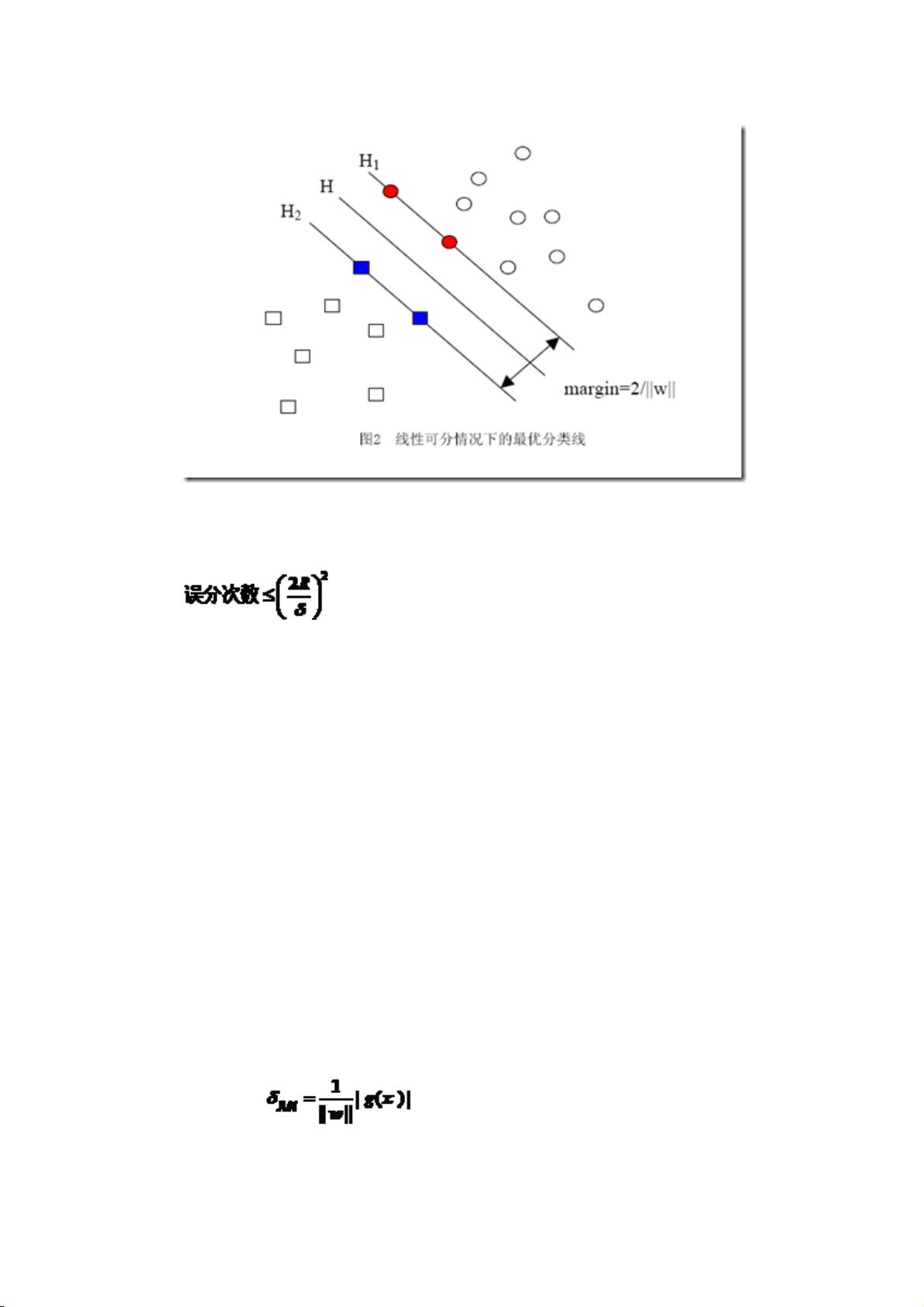
"支持向量机SVM是Cortes和Vapnik在1995年提出的一种非线性分类方法，具有处理小样本、非线性和高维数据的优势，广泛应用于模式识别和函数拟合。SVM基于统计学习理论的VC维理论和结构风险最小化原则，寻求最佳的模型复杂性和学习能力之间的平衡，以提升泛化能力。Vapnik的《Statistical Learning Theory》深入探讨了统计机器学习的思想，区别于传统机器学习的盲目实践。VC维衡量问题复杂度，而SVM对样本维数不敏感，适合处理高维文本分类问题。结构风险最小化是指在未知真实模型的情况下，选择最优化的假设模型来逼近问题的真实解。" 支持向量机（SVM）是一种强大的机器学习算法，主要用于二元分类和回归分析，但也可以通过扩展处理多类分类问题。其核心思想是构建一个最大边距超平面，将不同类别的数据点分离得尽可能远。在这个过程中，SVM特别关注那些距离超平面最近的数据点，即支持向量，这些点对于决定分类边界至关重要。 SVM的理论基础是Vapnik-Chervonenkis（VC）维，它量化了模型的复杂性。VC维高的模型可以表示更复杂的决策边界，但也可能导致过拟合，即对训练数据过度适应，而在未见过的新数据上表现不佳。为了克服这个问题，SVM采用结构风险最小化策略，通过正则化避免过拟合，同时追求良好的泛化性能。 在实际应用中，SVM引入了核函数这一关键概念。核函数能够将低维数据映射到高维空间，使得原本在原始空间中难以分隔的数据在高维空间中变得容易区分。常见的核函数有线性核、多项式核、高斯核（RBF）等，不同的核函数适用于不同的数据分布和问题情境。 除了上述理论，SVM在实际操作中还需要考虑一些重要因素，比如参数调整（如惩罚系数C和核函数的参数）、预处理（如特征缩放和缺失值处理）、以及选择合适的核函数。此外，对于大规模数据集，SVM的训练时间可能会很长，这时可以采用启发式方法或者核近似技术来提高效率。 总结来说，支持向量机SVM是一种基于统计学习理论的高效分类工具，它的优势在于处理非线性问题和高维数据，通过优化模型复杂性和泛化能力的平衡，以及利用核函数进行非线性映射，实现了在多种任务中的优秀性能。理解和掌握SVM的基本原理和应用技巧，对于机器学习领域的研究者和实践者来说都是至关重要的。