"线性代数的几何意义之二：向量的几何图形化解析"

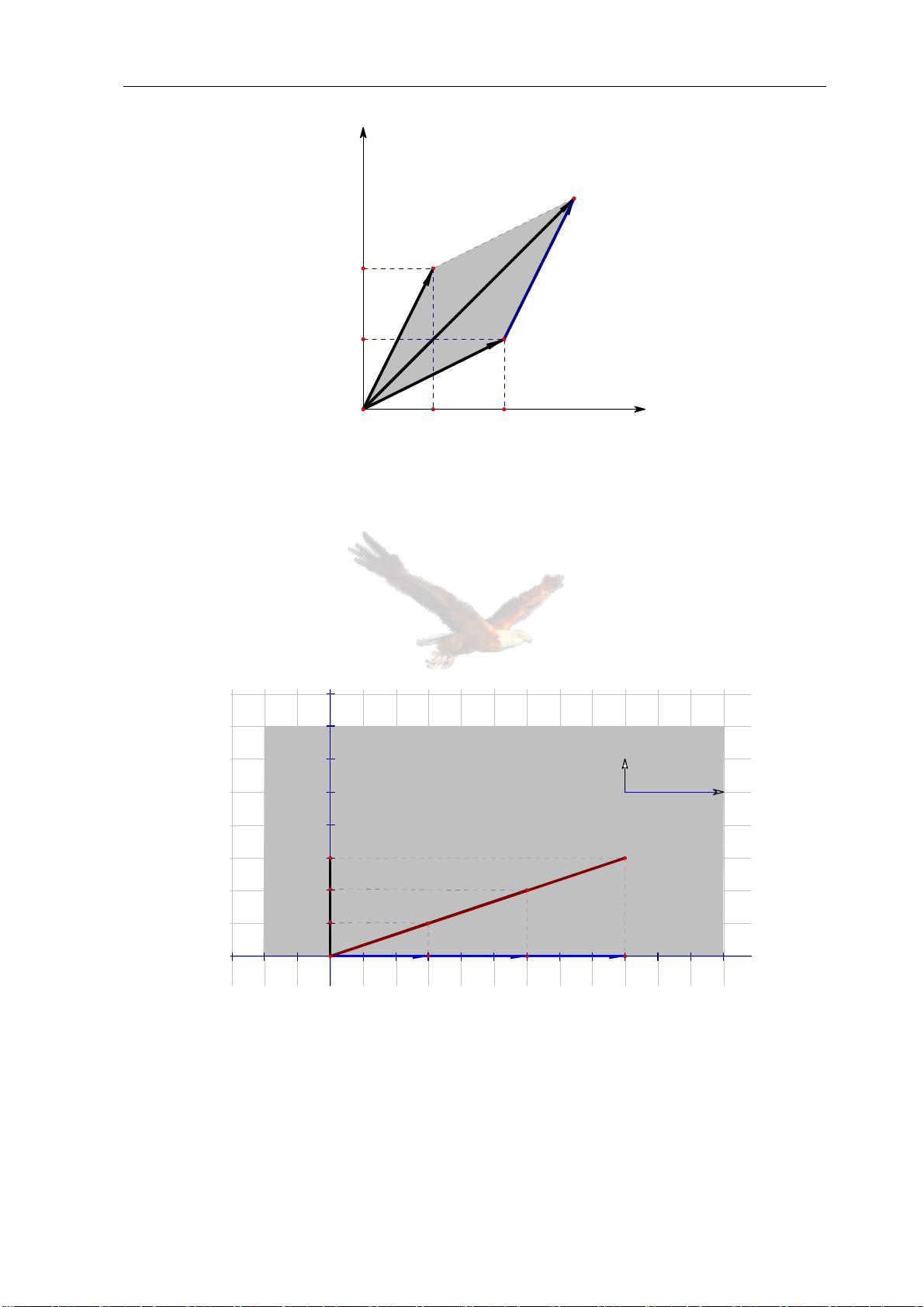
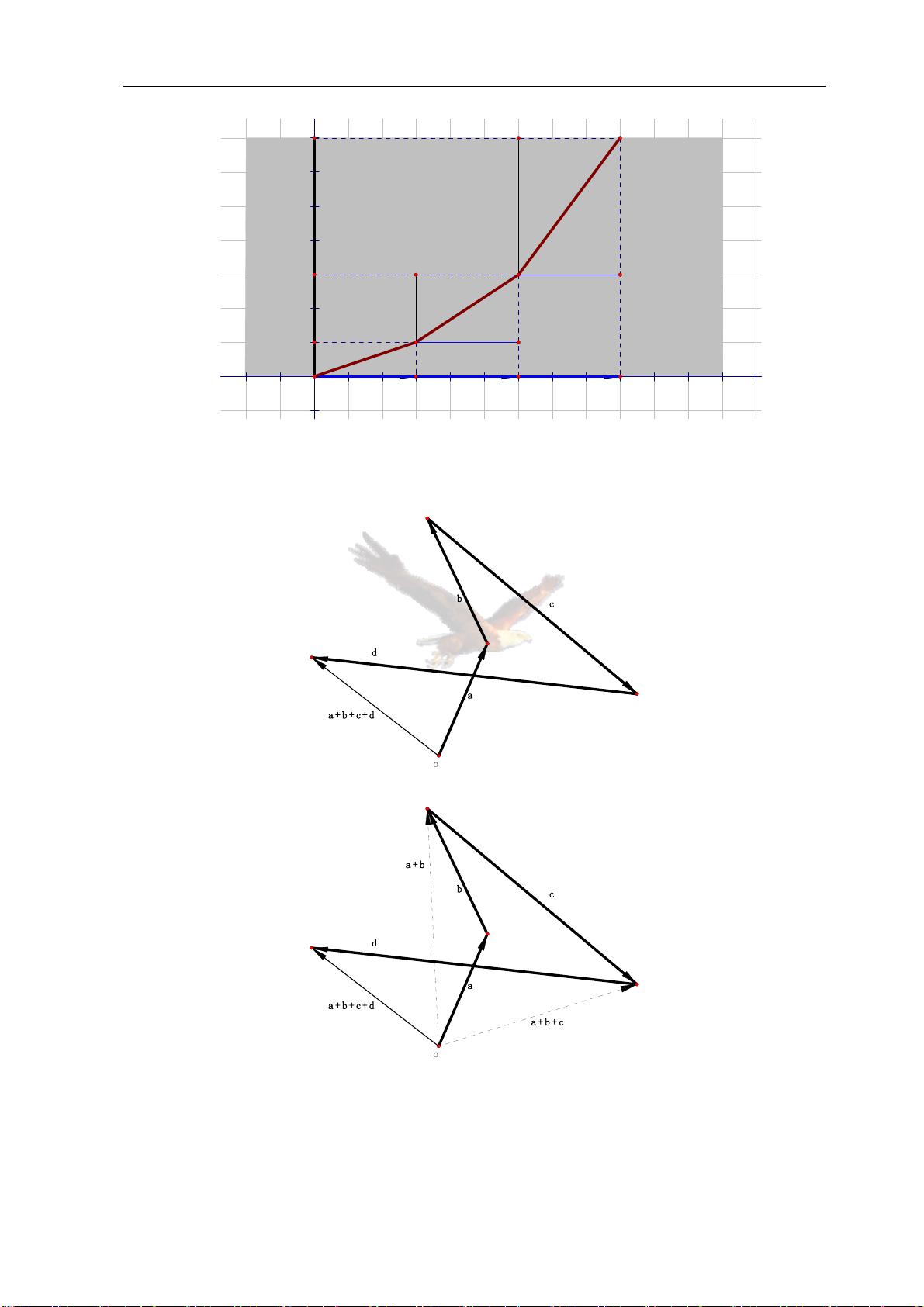
《线性代数的几何意义》之二(向量的几何意义) 在当代科学和线性代数的主要内容中，向量的概念始终贯穿其中。通过回顾向量的几何意义，我们可以更清晰地理解线性代数的重要概念。向量的基本几何意义在数学中起着至关重要的作用，它们不仅帮助我们理解数学原理，还可以解释许多物理现象和工程应用。因此，在这里我们将深入探讨向量的几何意义，并探讨其中蕴含的深层含义。 几何形状和图形是最容易被人们理解和记忆的事物，因为它们可以直观地展现出来。正如笛卡尔所说，算术符号是文字化的图形，而几何图形则是图像化的公式。数学家们在进行研究时，常常需要使用几何图形来帮助他们理解问题本质。而向量正是几何学中一个重要的概念，它能够用来描述空间中的方向和大小，从而帮助我们解决很多复杂的问题。 希尔伯特曾指出，没有一个数学家能够缺少图像化的公式。这句话体现了向量几何意义在数学研究中的重要性。在现代数学中，向量广泛应用于代数、几何、物理等领域，它们不仅是数学理论的基石，还是工程技术的重要工具。通过理解向量的几何意义，我们可以更好地应用它们解决实际问题。 拉格朗日曾说过，代数与几何互相结合发展，可以相互加强，并以快速的步伐向着完善的方向猛进。这表明了向量几何意义在数学领域中的重要作用。正是因为代数和几何的结合，我们才能够更全面地理解数学规律，并在实践中取得更大的成就。因此，学习和掌握向量的基本几何意义，对于我们提高数学水平和解决实际问题具有重要意义。 柏拉图曾指出，不会几何学就不会正确思考，而不会正确思考的人只是行尸走肉。这句话揭示了几何学在认知和思维中的重要性。通过学习向量的几何意义，我们不仅可以提高数学思维能力，还可以培养良好的逻辑推理能力。因此，向量的几何意义不仅是数学研究中的重要概念，还是培养学生综合能力的有效工具。 总之，通过深入理解向量的几何意义，我们可以更好地应用它们解决实际问题，提高数学思维能力，培养逻辑推理能力，从而取得更大的成就。因此，向量的基本几何意义在数学研究和工程实践中具有不可替代的作用，是我们学习和掌握的重要内容。愿我们能够深入理解向量的几何意义，并运用它们解决更多复杂的问题，为数学研究和科学发展做出更大的贡献。