空间统计学：球状模型与实验变差函数解析

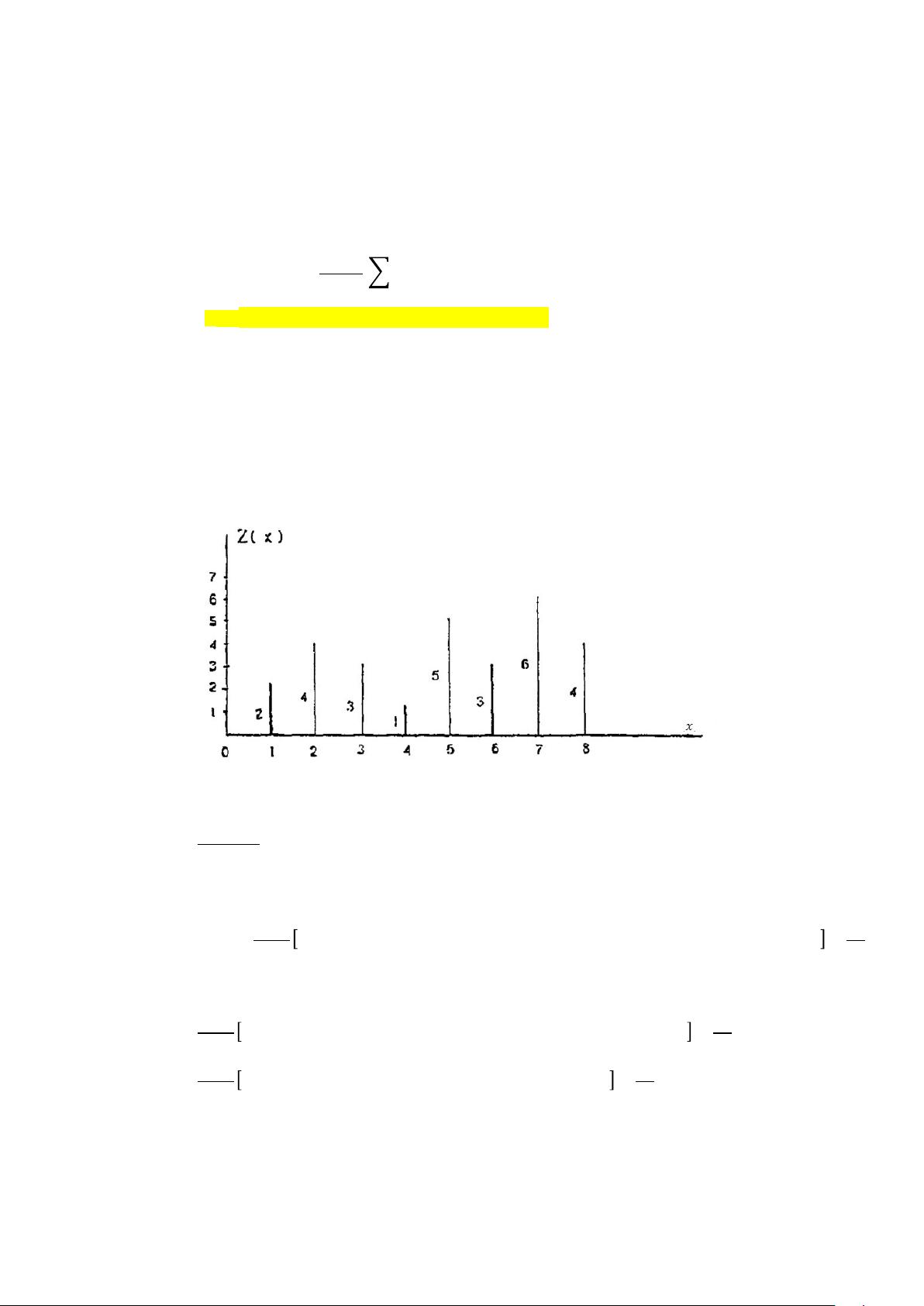
"本文主要介绍了球状模型在空间统计中的应用，包括实验变差函数的计算、变差函数与协方差函数的关系、克里金插值中的权系数确定，以及理论模型中的球状模型。此外，还通过实例解析了如何利用球状模型估计未知点的属性值。" 球状模型是一种广泛应用于地质学、环境科学和地球物理学等领域中的空间统计模型，用于描述数据的空间自相关性。实验变差函数是评估这种自相关性的关键工具，它衡量了不同位置数据点之间的差异。对于一维数据，实验变差函数可以通过计算相邻数据点对的差异来得到，滞后距h表示数据点之间的距离。 空间自相关性是指在一定距离范围内，数据点之间的值存在某种程度的相关性。这种相关性可以用半方差或半变异函数来度量，滞后距h则代表了这个相关性的最大距离，即变程。在球状模型中，变差函数在接近原点时呈线性增长，到达变程时达到一个基台值，这个基台值等于块金值（全局平均值）加上拱高（反映数据的随机波动部分）。 变差函数与协方差函数密切相关，因为二阶平稳性要求数据的均值恒定，协方差只依赖于两点间的位置。因此，可以将变差函数转换为协方差函数，通过求逆矩阵来确定克里金插值中的权系数。克里金插值是一种插值方法，旨在利用已知点的信息预测未知点的值，其关键在于权系数的计算，这些系数基于半方差或协方差函数的性质。 在具体应用中，如油藏孔隙度的估计，可以设定一个球状模型，根据已知井点的孔隙度值，利用球状模型公式计算出变差函数，进而估计目标点的孔隙度。在这个例子中，我们通过建立普通克里金方程组，并求解权重矩阵，从而得到目标点的估计值。 在矩阵表示中，权重系数的计算通常涉及半方差或协方差矩阵，这两个矩阵是等价的，因为它们都反映了数据点之间的相关性。在克里金插值过程中，权值矩阵的求解可以通过解线性方程组实现，这个方程组与数据的协方差结构紧密相关。 总结来说，球状模型提供了一种理解和模拟空间数据自相关性的有效方法，实验变差函数和克里金插值则是实际应用中的核心工具。通过这些理论和方法，我们可以更好地理解空间数据的分布模式，并预测未被观测到的区域的特性。