社交网络图的三角计数：MapReduce算法实现

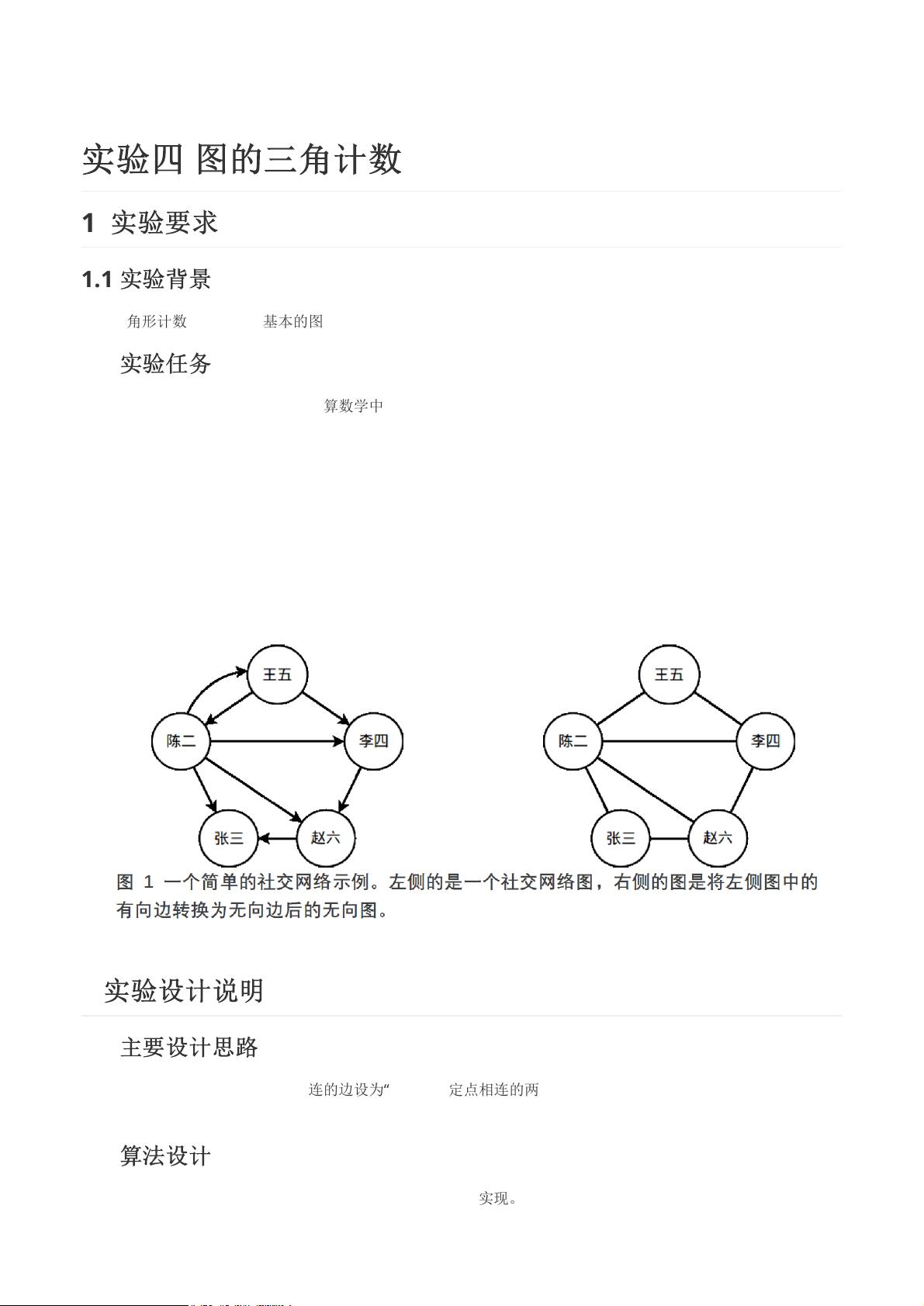
实验四：图的三角计数 在这个实验中，你将深入理解图论在社交网络分析中的应用，特别是三角形计数这一基础概念。三角形计数指的是在图中寻找由三个顶点形成的闭合路径，这些路径在社交网络中常常用来衡量用户间的紧密程度或社区结构。 **实验要求**： 1.1 **背景**：图的三角形计数是社交网络分析中的核心任务，因为它能反映用户的相互连接程度，有助于理解群体内的互动模式。例如，在Twitter这样的平台，关注关系构成了图，三角形代表三人共同关注的情况，揭示了潜在的兴趣群组。 1.2 **实验目标**：你的任务是在给定的社交网络图中，统计所有无向边构成的三角形数量。为了进行计数，你需要先将有向边转换为无向边，并遵循从有向边“A->B”到无向边“A-B”的逻辑。 **实验设计说明**： 2.1 **设计思路**：采用MapReduce编程模型，将三角形计数划分为三个步骤。首先，将有向边转化为无向边，并标记相邻节点的关系；其次，通过两次MapReduce操作，分别处理与选定点相邻的边和查找形成三角形的条件；最后，第三次Map阶段不进行任何处理，由Reduce阶段计算三角形数量。 2.2 **算法设计**： - **Map_1**：读取输入数据，整理成键值对（A+B，+），保证A小于B，用于去重。 - **Reduce_1**：去重后的键值对作为输入，输出键值对保持不变，为后续步骤做准备。 - **Map_2**：读取Reduce_1的结果，处理与指定点相连的边，形成键值对（A，B）和（A+C，+），同时查找是否存在边BC，若有，则添加键值对（B+C，-）。 - **Reduce_2**：根据Map_2的输出，对与指定点相关的边进行合并，检查是否存在形成三角形的条件。 - **Map_3**：不做处理，仅接收数据。 - **Reduce_3**：统计满足条件的“-”个数，即为三角形的个数。 在图1所示的简单例子中，由于三个顶点（如A、B、C）形成了三个三角形（ABC, ACB, BCA），在经过上述转换和计算后，会得出相应的三角形计数值。 总结，这个实验不仅锻炼了你对图论基础的理解，还提升了你使用MapReduce进行大规模数据处理的能力。在完成实验的过程中，你将掌握如何运用图的性质来分析社交网络中的结构和关系，并且能通过实际编程实现对复杂网络的三角计数。