马尔可夫链：现代概率论中的关联随机过程

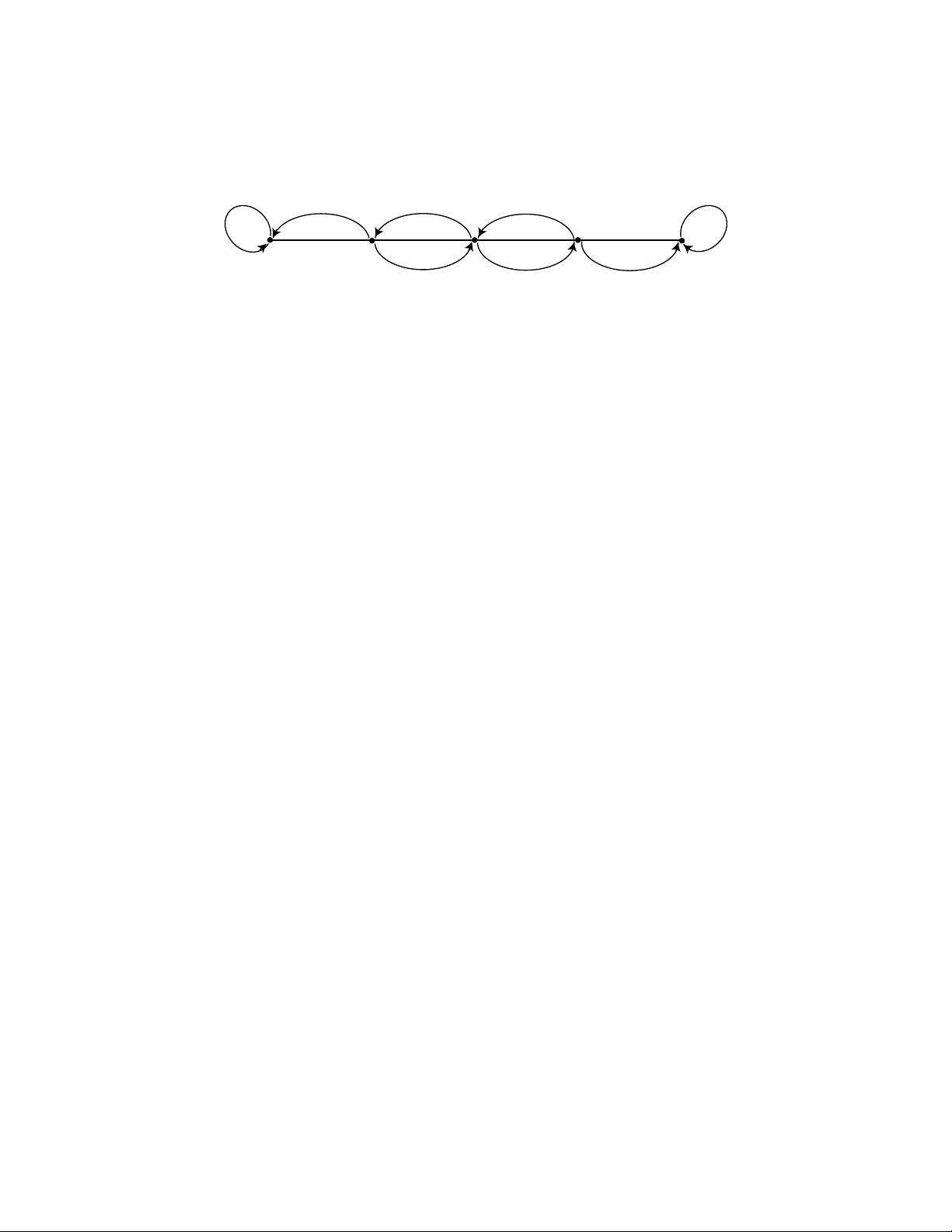
马尔科夫链（Markov Chains）是现代概率论中的一个重要概念，它与经典概率理论有所不同，专注于研究那些过去的结果会影响未来事件预测的随机过程。在传统的独立试验过程中，每个试验的结果是独立的，且每次实验的概率分布不变，如大数定律（Law of Large Numbers）和中心极限定理（Central Limit Theorem）所描述的那样。然而，马尔可夫模型假设当前状态只依赖于前一个状态，忽略了更远的过去历史，这是一种局部依赖性。 11.1 节的介绍部分阐述了马尔可夫链的基本原理。在马尔可夫模型中，虽然每次试验的可能结果保持一致，但对未来实验结果的预测不再受先前所有实验结果的影响，只需要知道当前的状态或最近一次的结果即可。这种特性使得马尔可夫模型能够通过构建状态转移图，也就是著名的马尔可夫链图，来刻画整个过程。树状结构被用来表示可能的状态序列及其相应的概率，通过计算节点间的转移概率，可以解决关于这些实验序列的各种概率问题。 在实际应用中，马尔科夫链广泛应用于各种领域，如自然语言处理中的语言模型、机器学习中的序列预测、生物信息学中的基因调控网络分析，以及通信网络中的信道状态预测等。例如，在天气预报中，明天的天气可能会受到今天的影响，但不会受到昨天甚至更早的天气状况的直接影响，这就是一个简单的马尔可夫模型示例。 马尔科夫链的核心在于其记忆性质，即“记忆长度为一”，这意味着模型的动态行为只依赖于当前位置，而过去的全部历史信息被视为已知的条件。这简化了复杂系统的建模和分析，使之成为解决具有时间相关性和有限记忆效果问题的有效工具。 马尔科夫链是一种强大的数学工具，它扩展了经典概率理论，引入了基于局部依赖性的随机过程，使得我们能够在众多领域中有效地处理序列依赖的问题，并通过树状结构和转移概率来计算相关事件的概率。理解并掌握马尔可夫链的方法论对于深入理解现代统计学和信息技术至关重要。