图论与遍历算法:无向图、搜索策略与网络可靠性
"图与遍历算法"
在计算机科学中,图是一种抽象数据结构,用于表示对象之间的关系。图论是研究这些结构的理论基础,它包括无向图、有向图、树和二叉树等概念。无向图是每个边连接两个顶点,而有向图中的边具有方向性,即从一个顶点指向另一个顶点。树是无环的图,而二叉树是一种特殊类型的树,每个节点最多有两个子节点。
图的遍历算法是图论中的核心概念,主要用于探索图的所有节点。二叉树的遍历有三种主要方法:先根次序(根-左-右),中根次序(左-根-右)和后根次序(左-右-根)。这些方法对于访问和处理二叉树的节点至关重要。对于一般树,遍历方式类似,但可能有更多的分支需要考虑。
图的搜索算法主要包括宽度优先搜索(BFS)和深度优先搜索(DFS)。BFS从起点开始,逐层访问所有邻居节点,而DFS则深入到图的深处,直到无法再深入才返回。这两种算法在解决许多实际问题,如寻找最短路径或判断连通性时都十分有用。
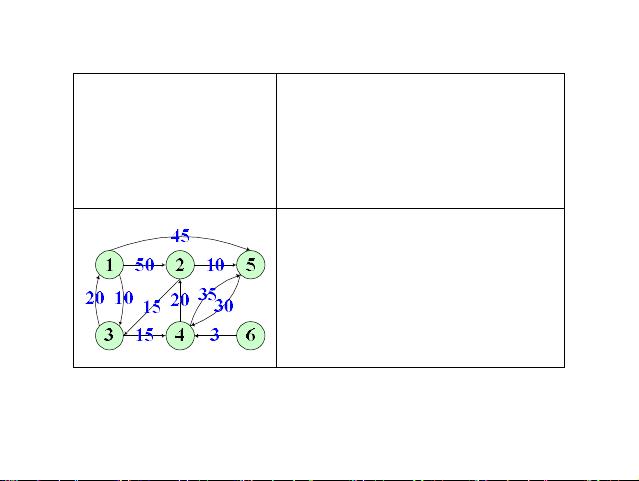
连通图的深度优先生成树和宽度优先生成树是用于确定图是否连通以及找到最小生成树的方法。连通图是指图中任意两个顶点间都存在路径。割点是指在删除后会导致图不连通的节点;双连通图是即使去掉任意一个节点仍然保持连通性的图。双连通分支算法可以用来找出这样的结构,这对于分析通信网络的稳定性非常重要。
通信网络的可靠性问题关注的是网络在部分故障或断开连接时仍能保持功能的能力。割点和双连通性分析是评估网络稳定性和设计容错策略的关键工具。
代码最优化问题通常涉及算法和数据结构的选择,以提高程序的运行效率。这可能包括减少时间复杂度、空间复杂度,或者通过并行化和优化内存管理来提升性能。
邻接矩阵和关联矩阵是表示图的两种矩阵方法。邻接矩阵是一个二维数组,其中的元素表示两个顶点之间是否存在边,而关联矩阵则记录了边与顶点的关系,通常用于有向图。这两种矩阵都是进行图操作和计算的基础,如计算路径、检测环路等。
图与遍历算法是计算机科学中的基本概念,它们在各种领域,如网络设计、数据结构分析、编译器优化等都有着广泛的应用。理解和掌握这些知识对于解决问题和开发高效算法至关重要。
2022-05-06 上传
2009-11-11 上传
2013-07-04 上传
2010-03-31 上传
220 浏览量
点击了解资源详情
点击了解资源详情
点击了解资源详情
jiao_luo
- 粉丝: 0
- 资源: 18
最新资源
- Aspose资源包:转PDF无水印学习工具
- Go语言控制台输入输出操作教程
- 红外遥控报警器原理及应用详解下载
- 控制卷筒纸侧面位置的先进装置技术解析
- 易语言加解密例程源码详解与实践
- SpringMVC客户管理系统:Hibernate与Bootstrap集成实践
- 深入理解JavaScript Set与WeakSet的使用
- 深入解析接收存储及发送装置的广播技术方法
- zyString模块1.0源码公开-易语言编程利器
- Android记分板UI设计:SimpleScoreboard的简洁与高效
- 量子网格列设置存储组件:开源解决方案
- 全面技术源码合集:CcVita Php Check v1.1
- 中军创易语言抢购软件:付款功能解析
- Python手动实现图像滤波教程
- MATLAB源代码实现基于DFT的量子传输分析
- 开源程序Hukoch.exe:简化食谱管理与导入功能