面向对象程序的图基泛型类型系统

196 浏览量更新于2024-07-15 收藏 751KB PDF 举报

“A graph-based generic type system for object-oriented programs”探讨了一种基于图模型的面向对象程序的泛型类型系统，该系统支持递归类型、泛型和接口等现代面向对象语言（如Java）常见的特性。通过经典图论，定义了类型图、实例化图和结合图，直观地展示了复杂面向对象程序中类型、泛型和接口之间的关系。模型采用名义节点和匿名节点的组合，分别表示由名称标识的类型和结构，并定义了基于图的关系和操作，包括等价性、子类型和构造。在面向对象编程（OO programs）中，类型系统是至关重要的，它确保了代码的正确性和安全性。本文提出的图基类型系统（graph-based type system）旨在增强这种类型检查，特别是对于具有泛型和接口的复杂程序。泛型（generics）允许在不牺牲类型安全性的前提下，创建可重用的代码，而接口（interfaces）则定义了类必须实现的方法，提供了多态性。类型图（type graphs）是这个模型的核心部分，它们代表了程序中的各种类型以及它们之间的关系。这些图可以清晰地描绘出类型层次结构，包括继承和实现关系。实例化图（instantiation graphs）则用于表示泛型类型的实例化过程，即如何将泛型参数替换为具体的类型。结合图（conjunction graphs）可能用来展示多个接口或类型的组合情况，这在实现多重继承或接口实现时特别有用。模型中，名义节点（nominal nodes）用于表示通过名称标识的类型，比如类或命名的接口。另一方面，匿名节点（anonymous nodes）则表示结构相似但未被明确定义的类型，例如匿名类或内部类。这样的区分使得类型系统能更好地处理动态类型和结构类型的情况。此外，文章还讨论了类型间的等价性（equivalence）、子类型关系（subtyping）和构造（construction）等概念。等价性确保了不同类型但逻辑上相等的实例可以互换使用；子类型关系允许子类的对象可以被当作父类来使用，增强了代码的灵活性；构造则是指如何通过现有的类型构建新的类型，这在泛型和接口的组合中尤其关键。通过这种图模型，开发者和编译器可以更有效地理解和验证程序中的类型行为，从而减少类型错误并提高代码质量。该模型对于编译器设计、类型检查算法和静态分析工具有着重要的理论和实践价值。同时，它也为面向对象语言的进一步发展和优化提供了新的研究方向。

Wei KE et al. A graph-based generic type system for object-oriented programs 113

and the frame of a method consists of the parameters of the

method. These structures are also characterized in a type

graph. In fact, each type, static table or method frame of a

program is represented as a subgraph of the type graph of

the program. There is a designated node in such a subgraph,

called the root of the graph of the type, static table or method

frame. For a nominal type, the root of its graph is the name of

the type, while for a structural type, a static table or a method

frame, the root is anonymous. We call the root of a nomi-

nal type a nominal node and an anonymous root a structural

node.

We use D to denote the primitive type (data type) names

and U the class (user type) names, and C = D∪Uthe type

constants. Let X be the type variables. Thus, C∪Xis the set

of nominal nodes. Using S to denote the structural nodes and

assuming all these sets are mutually disjoint, we have the set

N = C∪X∪Sof nodes of type graphs.

For the labels of edges, let A be the set of the names of

variables, attributes, methods and parameters, which is dis-

joint with N. We introduce a special label “” for the class

inheritance relation, and another special symbol “σ” to label

an incoming edge to the root of a static table. If a class con-

tains a type variable α, the class is generic. A generic class

can be instantiated by mapping α to some actual type u.We

use an edge labeled by the type variable α and targeting u to

record the mapping α → u. We put such an edge to the static

table of each generic class and class instantiation, see Fig. 1.

Thus, A

= A∪X∪{,σ} is the set of all labels of edges.

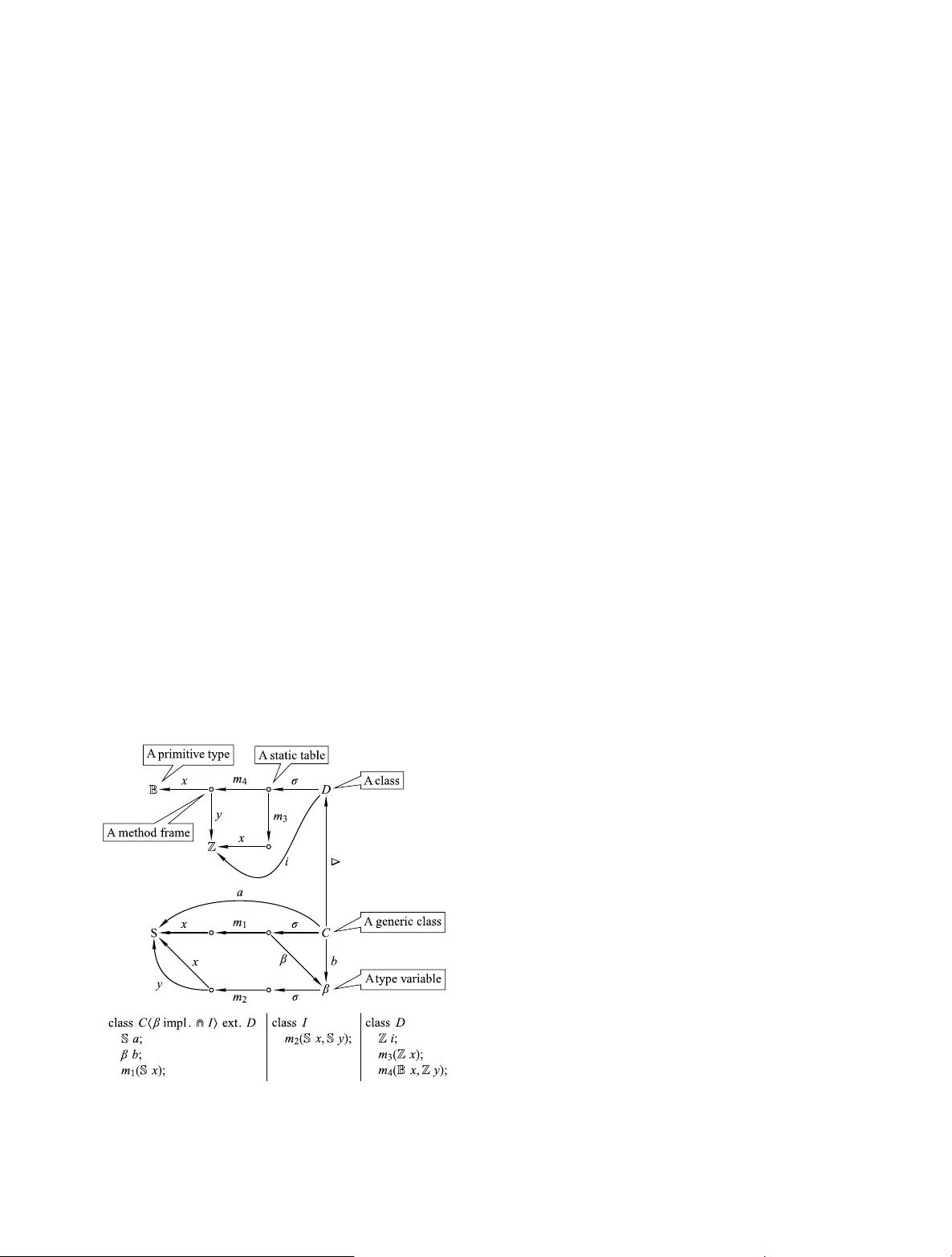
Fig. 1 A type graph and the corresponding class declarations

Deﬁnition 1 (Type graph) A type graph is a directed and

labeled graph Γ=N, E,whereN ⊆Nis the set of nodes,

and E : N ×A

→ N is the set of edges.

Notice that E is a function implies that labels of the out-

going edges of a node are distinct. Thus the names of at-

tributes and methods of a class are diﬀerent, and parameters

of a method are diﬀerent. In particular, there is no multiple

inheritances allowed in this model.

Figure 1 shows a type graph and the corresponding class

declarations. In the graph, C is a generic class, with a type

variable β and a superclass D. Notice the β-labeled edge tar-

geting at the node β.Ifβ is instantiated to an actual type,

the β node is replaced by the node of the actual type. C has

two attributes a and b of types S and β, respectively, and a

method m

with a parameter x of type S. The type variable β

implementing class I has a method m

with two parameters

x and y both of type S, meaning that any replacement of β in

an instantiation of C must deﬁne such a method. D is a non-

generic class with an attribute i and two methods m

and m

where m

has a parameter x and m

has two parameters x and

We use s

−→ t to represent an a-labeled edge from s to t,

and call s the source node and t the target node of the edge.

We use s

−→·to represent an a-labeled outgoing edge of s

and ·

−→ t an a-labeled incoming edge to t. For a given graph

Γ=N, E,weuseΓ.ns to denote the set N of nodes, and

Γ.es the set E of edges.

Apathp is a sequence of consecutive edges, denoted as

−→ n

···n

k−1

−→ n

or simply n

···a

−−−−−−→ n

, if we are not

concerned with its intermediate nodes. We also overload the

notation of set membership “∈”, using n ∈ Γ, e ∈ Γ and p ∈ Γ

to denote that a node n, an edge e and a path p are in graph Γ,

respectively.

For a path p,letsource (p)andtarget (p) be the starting

and ending node, respectively. We say that a node n

is reach-

able from a node n

, denoted as n

−→

∗

,ifthereisapath

from n

to n

.Apathn

−→ ···

−→ n

is simply denoted as

−→

∗

3.2 Rooted graphs

In the type graph Γ of a program, an individual type T,say

a class, is represented by a node r of Γ, the nodes reachable

from r and the edges between these nodes. These nodes and

edges form a subgraph of Γ with r being designated as the

root. This rooted graph represents the type T.

Deﬁnition 2 (Rooted graph) Given a node r of a graph Γ,

the rooting operation Γ  r returns the subgraph G = N, E, r

of Γ such that

N = {n | r −→

∗

n ∈ Γ},

114 Front. Comput. Sci., 2013, 7(1): 109–134

E = {n

−→ n

∈ Γ | n

, n

∈ N}.

This subgraph is called a rooted graph, where r is the root,

denoted as G..

Notice that for each node r ∈ Γ, Γr is unique. For a rooted

graph G = N, E, r, the graph N, E is called the base graph

of G, denoted as G.base . A path in G from the root r

−→ n is

denoted as 

−→ n. We extend the rooting operation to rooted

graphs, and deﬁne G  n ˆ= G.base  n.

The rooting operation performs garbage collection. For ex-

ample, a removal of a set es of edges from a rooted graph

G = N, E, r is deﬁned as

G  es ˆ= N, E  esr. (1)

The removal of edges may disconnect a subgraph from the

root, causing additional nodes and edges to be removed.

3.3 Type-equivalence

Relations between types can now be studied by comparing

the structures of their rooted graphs. Graph homomorphisms

are the instruments for this purpose. In addition to the con-

ventional graph homomorphism, which preserves outgoing

edges of each node, root nodes are also preserved in our case.

Deﬁnition 3 (Homomorphism) Given two rooted graphs

G = N, E, r and G



= N



, E



, r



, a function f : N → N



a homomorphism from G to G



, denoted as f : G → G



,if

−→ t ∈ E =⇒ f (s)

−→ f (t) ∈ E



, and f (r) = r



A node, the name of the node in particular, together with

the entire set of its outgoing edges is considered the structure

of the node. If this structure of a set of nodes does not change

under a homomorphism, we say the structure is preserved by

the homomorphism.

Deﬁnition 4 (Structural preservation) Let G and G



two rooted graphs. A homomorphism f : G → G



is a struc-

tural preservation on a set P ⊆ G.ns of nodes, if ∀n, n



∈ P

such that

n ∈C∪X =⇒ f (n) = n, f (n) = f (n



) =⇒ n = n



n ∈S =⇒ f (n) ∈S, f (n)

−→·∈G



=⇒ n

−→·∈G.

Notice that a structural preservation is diﬀerent from a

subgraph isomorphism, in that the latter does not consider

those edges going outside the subgraph. Obviously, a struc-

tural preservation on the entire node set of a graph is a graph

isomorphism preserving nominal nodes.

Deﬁnition 5 (Structural equivalence) Two rooted graphs

G and G



are structural equivalent, denoted as G  G



,if

there exists a structural preservation f : G → G



on G.ns.

However, the structural equivalence relation does not han-

dle the equivalence between a recursive structural type, in

which an attribute refers back to its owner type, and the un-

folded variants of the recursive type, as shown in Fig. 2.

For this, we deﬁne the type reduction relation, which al-

lows structural nodes with the same set of outgoing edges

to be merged, so as to have a graph possibly mapped to its

subgraph. That is, we remove the 1-1 property for structural

nodes from the conditions of Deﬁnition 4.

Fig. 2 Equivalent recursive types

Deﬁnition 6 (Reduction) A rooted graph G is reducible to

a rooted graph G



, denoted as G  G



, if there exists a ho-

momorphism f : G → G



such that ∀n ∈ G,

n ∈C∪X =⇒ f (n) = n,

n ∈S =⇒ f (n) ∈S, f (n)

−→·∈G



=⇒ n

−→·∈G.

We call such f a reduction function.

Deﬁnition 7 (Type-equivalence) Two rooted graphs G and



are type-equivalent, denoted as G ∼ G



, if there exists a

rooted graph G

such that both G and G



are reducible to G

It is straightforward to verify that ∼ is an equivalence rela-

tion. In addition, G ∼ G



holds if and only if there exist G

and G



such that G is reducible to G

, G



is reducible to G



and G



are structural equivalent, i.e., G

 G



In general, we use Γ  n♦ n



to denote that two rooted

graphs Γ  n and Γ  n



are related by a relation ♦ , i.e.,

Γ  n♦ Γ  n



. We also say the two nodes n and n



have re-

lation ♦ . In particular, two nodes n and n



in a type graph Γ

are called type-equivalent if Γ  n ∼ n



It is worth pointing out that if two types T and T



are equiv-

alent, attributes of T and T



with the same names also refer

剩余25页未读，继续阅读

weixin_38657376

粉丝: 4
资源: 928

面向对象程序的图基泛型类型系统

Graph-Based Semi-Supervised Learning

（ 源代码）GMC: Graph-based Multi-view Clustering

A Tutorial on Graph-Based SLAM

IC的STA中的Graph-Based Analysis和Path-based analysis的区别是什么

STA中的Graph-Based Analysis

IC 中的STA中的Graph-Based Analysis

efficient graph-based im- age segmentation baidu xueshu

Graph-based discriminative features learning for fine-grained image retrieva

Change Detection From Synthetic Aperture Radar Images via Graph-Based Knowledge Supplement Network讲解

GRAPH-RELATIONAL DOMAIN ADAPTATION

最新资源

（源代码）GMC: Graph-based Multi-view Clustering