后序遍历与Catalan数：递推算法实例解析

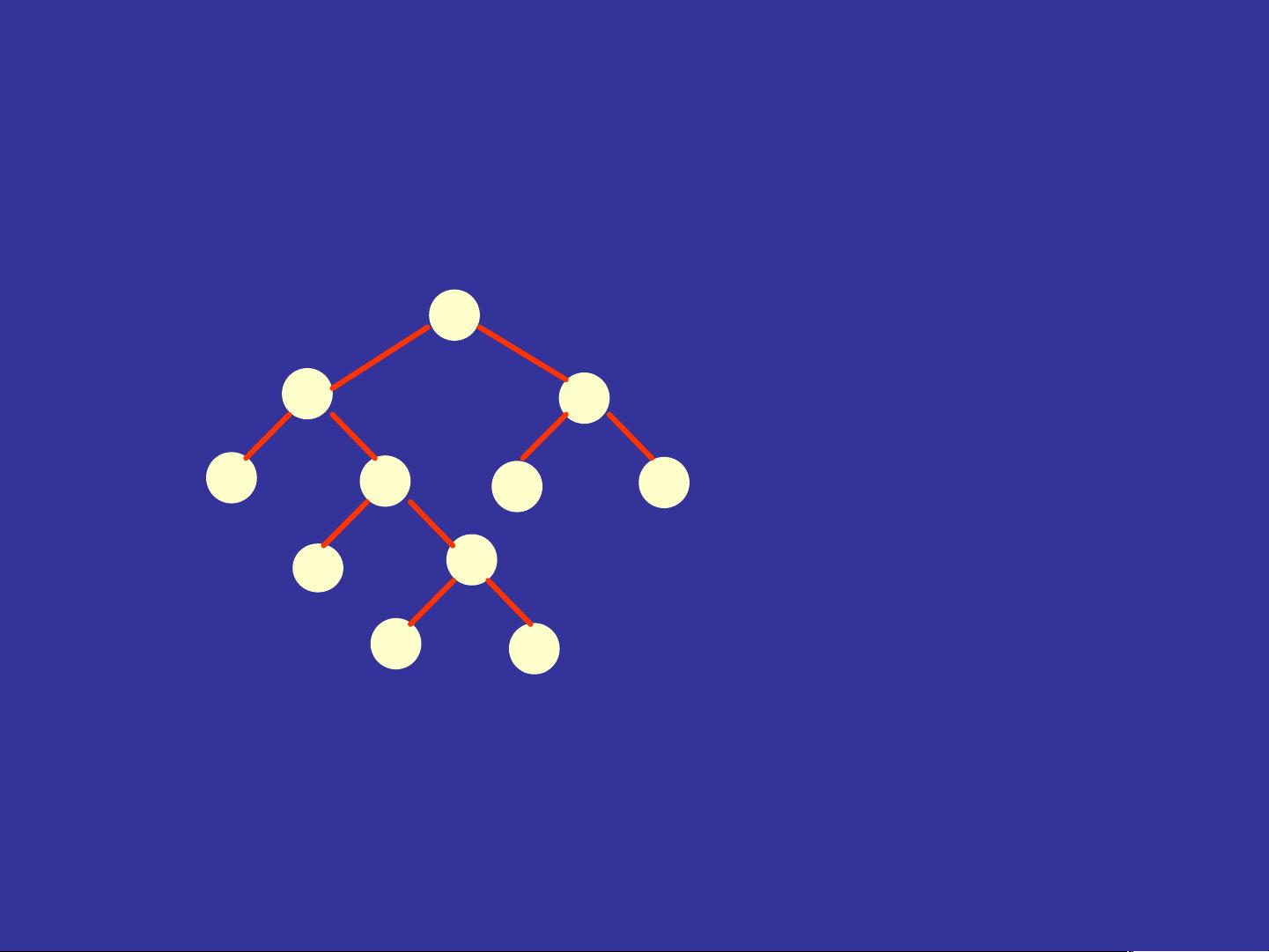
后序遍历（LRD）是一种用于二叉树的遍历策略，当需要按照左子树、右子树、根节点的顺序访问所有节点时，它适用于深度优先搜索。在执行后序遍历时，首先递归地遍历左子树，接着遍历右子树，最后访问根节点。这种遍历顺序对于某些问题的解决很有帮助，比如构建表达式树或者在计算机科学中进行特定数据结构的处理。 Catalan数是一个重要的数学概念，在算法和组合数学中有着广泛应用。它们定义为满足递归公式 \( h(n) = h(0) \cdot h(n-1) + h(1) \cdot h(n-2) + \ldots + h(n-1) \cdot h(0) \)，其中 \( n \geq 2 \)，并且具有性质 \( h(n) = \frac{1}{n+1} \binom{2n}{n} \)。Catalan数常用于解决与平衡括号配对、路径形成、二维多面体等问题，其中关键在于找到问题与Catalan数递归式的对应关系。 在某些信息学问题中，特别是涉及栈操作和操作序列的问题，Catalan数的模式可以帮助我们简化问题。例如，当考虑如何排列A和B元素，使得B的数量不超过A的数量，这个问题可以通过将操作序列映射到二进制数的形式来转化为Catalan数问题。在这种情况下，我们需要找到那些在任何位置上“0”的累计数量都不超过“1”的累计数量的二进制序列，这正是Catalan数的特性体现。 至于二叉树的计数问题，例如计算具有N个节点的不同形态的二叉树数目，这是一个经典的组合问题。这里提到的二叉树定义强调了每个节点最多有两个子树，且左右子树不能颠倒，这体现了二叉树的有序性。求解这类问题时，通常会利用递归的方法，通过定义二叉树的生成函数或递推公式来计算所有可能的树结构。 总结来说，后序遍历LRD和Catalan数是IT领域中两个紧密相关的概念，它们在算法设计和数据结构分析中扮演着重要角色。理解并掌握这些技巧有助于解决一系列复杂的问题，尤其是在处理动态规划、递归和组合优化等问题时。