机器人运动学方程解析：欧拉角与A矩阵

"大学机器人教程第03章 运动学方程.ppt" 在本大学机器人教程的第三章中，主要探讨的是机器人的运动学方程，这是理解机器人操作的关键概念。运动学主要关注机器人各个部分如何通过空间移动和转动来达到特定位置和姿态，而不涉及动力学因素。这一章涵盖了多个重要主题，包括引入运动学方程、姿态描述、欧拉角以及不同类型的机器人运动方程。 首先，章节介绍运动学方程的基础，利用齐次变换矩阵（A矩阵）来描述机械手在不同坐标系中的位置和方向。A矩阵代表了相邻连杆之间的相对平移和旋转，是构成总变换矩阵T的基础。例如，对于具有六个自由度的机械手（通常指六关节机器人），其总变换矩阵T6由六个A矩阵的乘积组成，即T6=A1A2A3A4A5A6。这个T6矩阵包含了机械手在基坐标系中的完整位置和姿态信息，由三个旋转向量n、o、a和一个平移向量p共同定义。 接着，详细讨论了如何指定机器人的姿态。T6矩阵的16个元素分别对应于旋转和位移的信息。为了完全定义T6，需要确保旋转向量o和a是正交的单位向量，并且通过交叉乘法得到第三个正交向量n。通过调整o和a，可以构建出与这三个向量相正交的完整坐标系，从而精确地描述末端执行器的位置和方向。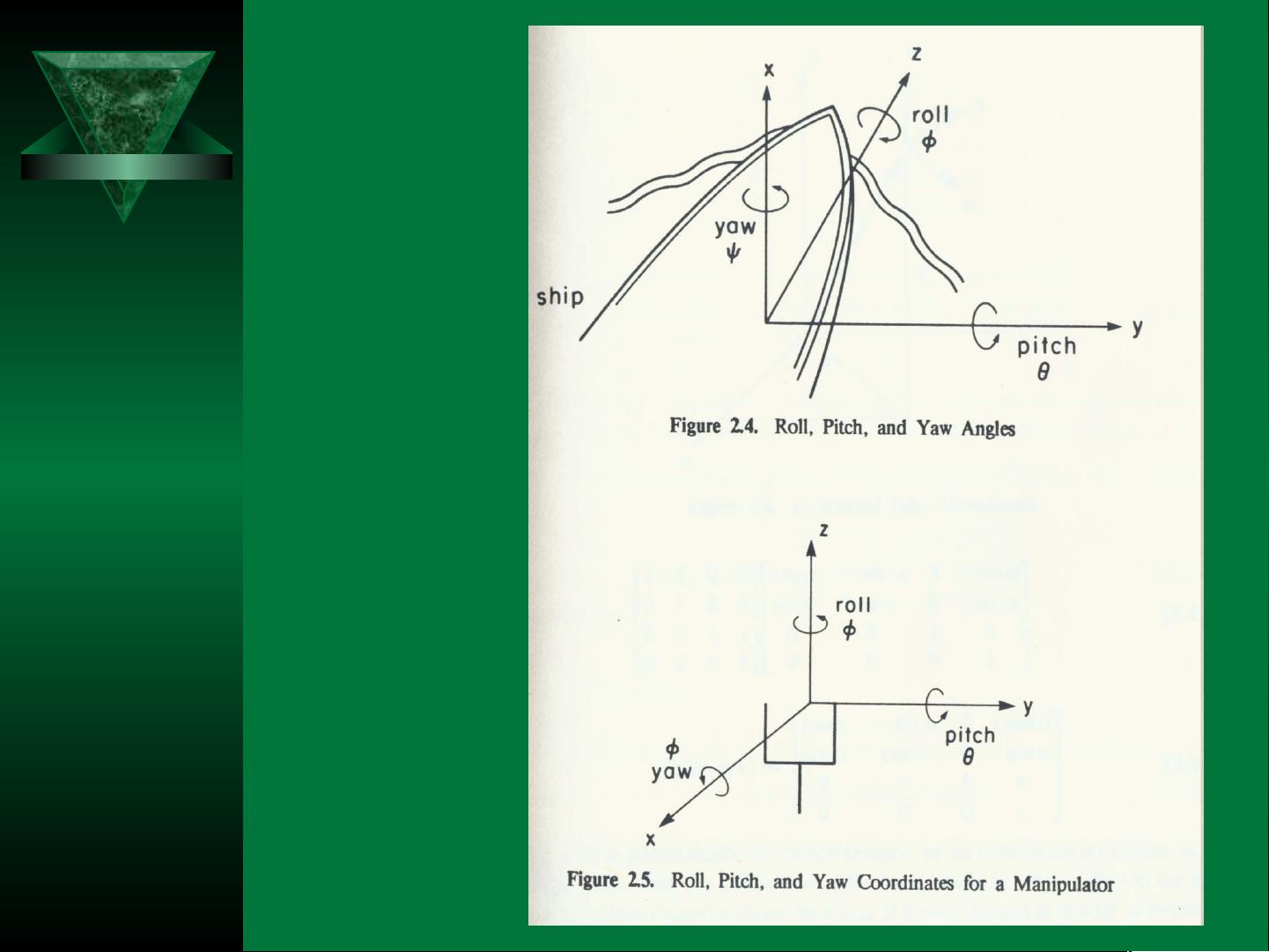 在姿态描述部分，欧拉角被引入作为一种常见的表示方法。欧拉角通常由三个旋转组成，依次围绕x、y'（原y轴旋转后的新y轴）和z''（再次旋转后的z轴）轴进行。这三步旋转的组合形成了一个Euler(ø,θ,ψ)变换，可以通过三个旋转矩阵的连乘来计算。欧拉角提供了直观的方式来描述三维空间中的连续旋转，常用于机器人控制和路径规划。 此外，本章还涉及了不同类型的机器人运动方程，包括斯坦福机械手和肘关节机械手的运动方程。这些方程展示了如何将关节角度转换为末端执行器的实际位置和姿态。每个机械手因其结构的不同，其运动方程也会有所不同，但都基于相同的运动学原理。 这一章深入浅出地讲解了机器人运动学的核心概念，为理解机器人控制系统和路径规划奠定了坚实的基础。学习者可以通过掌握这些知识，进一步探索更复杂的机器人运动控制策略。