时间序列分析：预测技术与模型

"时间序列模型是用于分析按时间顺序排列并随时间变化的数据序列的统计方法。这种模型在数据分析中占据重要地位，特别是在预测和理解数据动态行为时。时间序列可以分为一元和多元，离散和连续，平稳和非平稳，以及高斯和非高斯型。平稳时间序列具有恒定的均值和仅依赖于时间差的协方差，而宽平稳时间序列是统计特性不变的时间序列。时间序列的变化通常由长期趋势、季节性、循环变动和不规则变动组成。确定性时间序列模型包括加法模型、乘法模型和混合模型，分别通过不同方式组合这些成分来表示时间序列。移动平均法是一种常用的技术，通过计算序列的滚动平均来揭示长期趋势，适用于随机变动小且趋势稳定的序列。" 时间序列分析是数据分析的一个关键分支，它涉及处理按时间顺序排列的数据，这些数据在时间上是相关的。时间序列可以分为两类：一元时间序列关注单一变量随时间的变化，而多元时间序列则涉及多个变量。时间序列的连续性又可分为离散和连续，前者是基于特定时间点的数据，后者则涉及连续时间间隔的采样。 在统计特性方面，时间序列被划分为平稳和非平稳序列。平稳时间序列的统计性质如均值和方差是时间独立的，而宽平稳时间序列则保持其一阶和二阶矩不变，协方差仅与时间差有关。在实际应用中，宽平稳时间序列更为常见，也是许多模型构建的基础。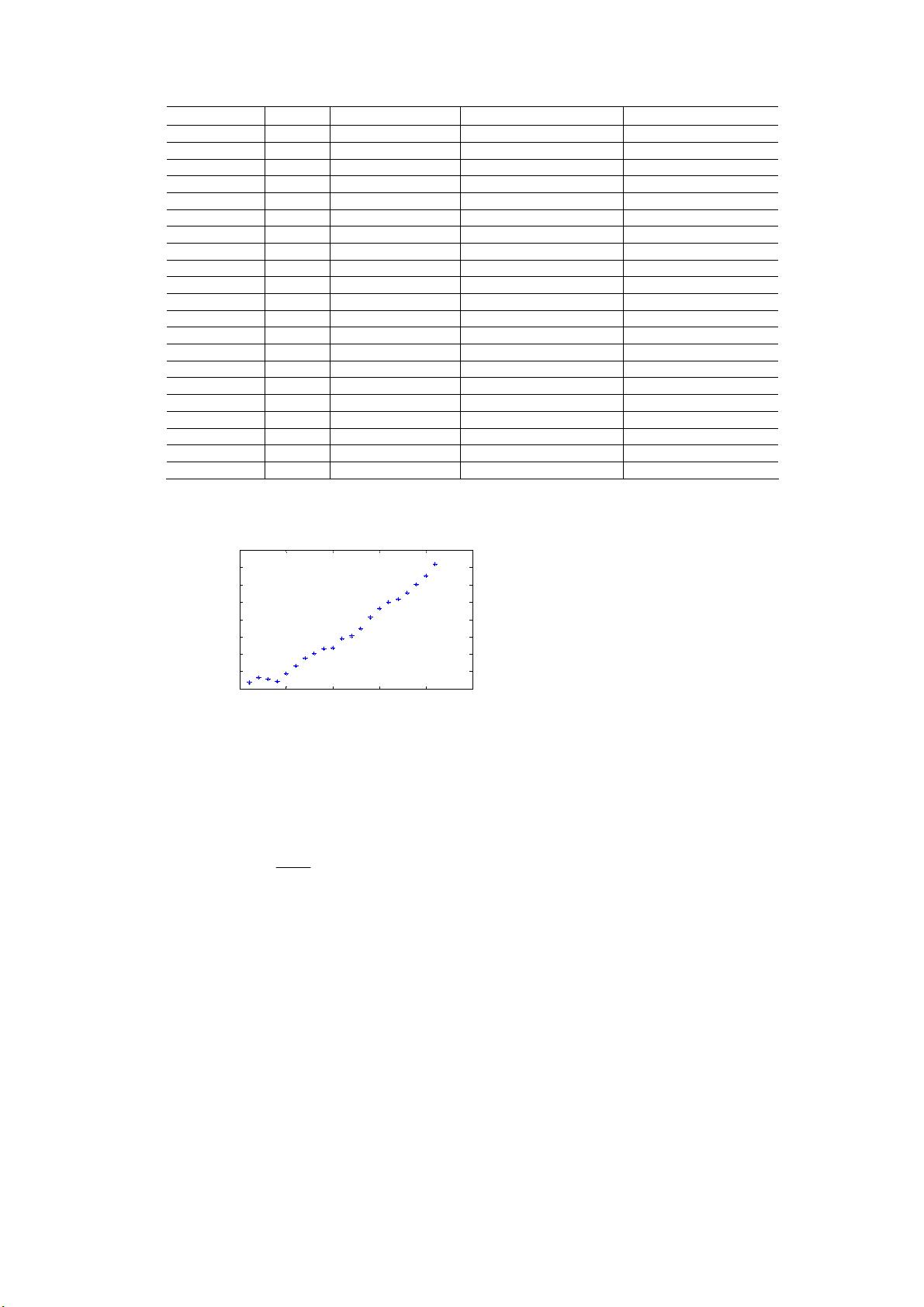 时间序列的动态变化通常由四个主要成分构成：长期趋势，表现为数据的持续上升或下降；季节性，与特定周期（如一年四季）相关的变化；循环变动，指周期超过一年的非季节性波动；以及不规则变动，包括突然变动和随机变动，这两者都难以预测。 确定性时间序列模型是用于分析和预测这些变化的工具。加法模型假设各成分相加，乘法模型认为各成分相互影响，而混合模型则是两者的结合。这些模型可以帮助我们理解和分离出时间序列中的各个重要因素，以便进行预测。 移动平均法是一种简单但实用的确定性时间序列分析方法，主要用于识别和过滤短期波动，突出显示长期趋势。这种方法通过计算序列中连续项的平均值，形成一个新的平滑序列，从而去除随机扰动，揭示出潜在的趋势。移动平均法在随机变动不大且趋势稳定的时间序列中尤为有效。 时间序列模型是理解和预测时间相关数据的关键工具，涵盖了广泛的概念和技术，从基本的平稳性和季节性分析到复杂的模型构建和预测策略，都是数据分析和决策制定过程中的重要组成部分。