"1999年全国31省消费水平的无监督聚类分析"

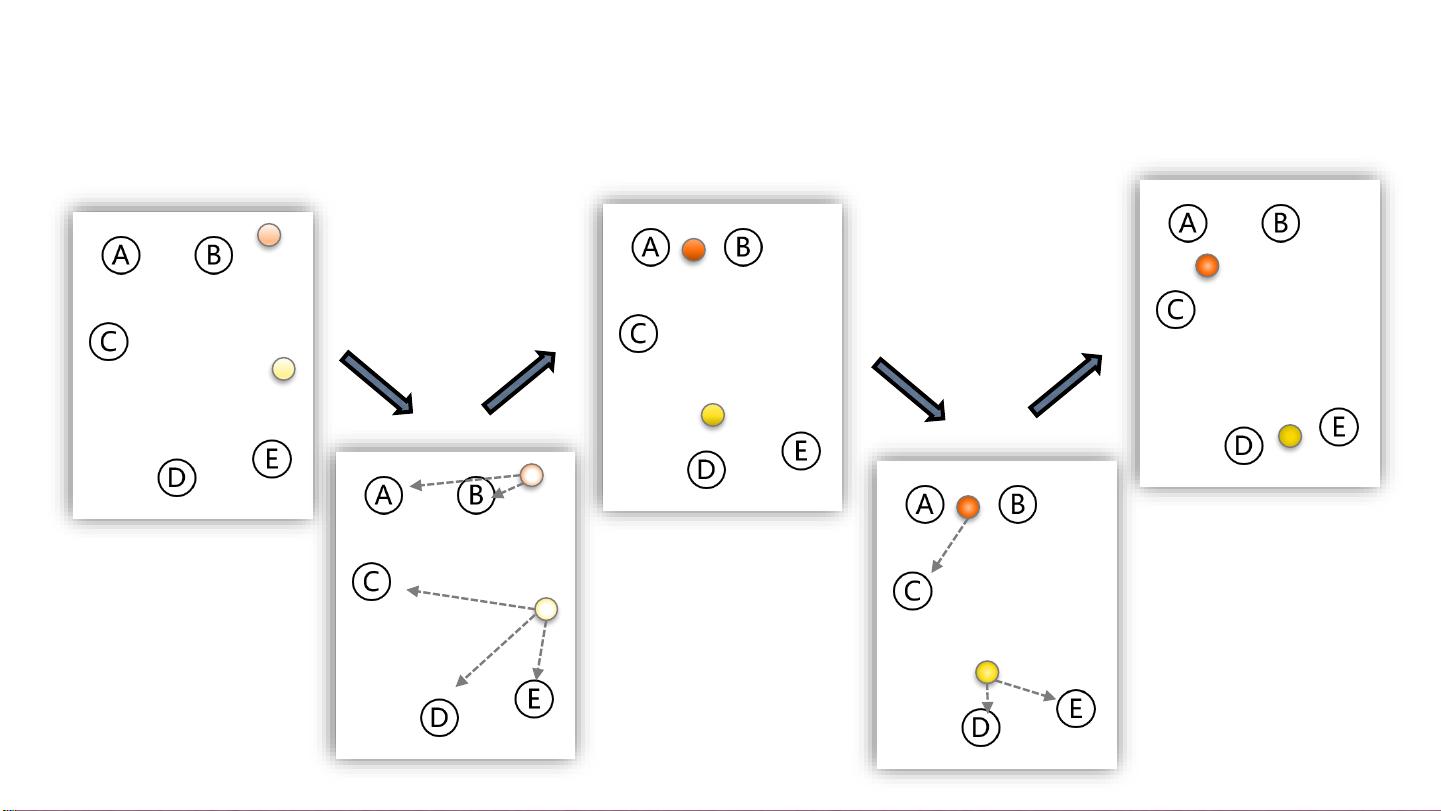
K-means是一种常用的无监督学习算法，用于对数据进行聚类。聚类是将具有相似特征的样本划分到同一个组或簇中，从而实现对数据的分组和分类。K-means算法以k为参数，将n个对象划分为k个簇，使得簇内的样本具有较高的相似度，而簇间的相似度较低。 其处理过程如下： 1. 随机选择k个点作为初始的聚类中心。在K-means算法中，一般是从样本集中随机选择k个样本作为初始的聚类中心点。 2. 对于剩下的点，根据其与聚类中心的距离，将其归入最近的簇。通过计算样本点与各个聚类中心的距离，将每个样本点归入与之最近的簇。 3. 对每个簇，计算所有点的均值作为新的聚类中心。通过计算每个簇中所有样本点的均值，得到新的聚类中心。 4. 重复2、3步骤，直到聚类中心不再发生改变。当聚类中心不再发生改变时，即每个样本点都与最近的聚类中心对应，则算法收敛，聚类过程结束。 K-means算法具有一定的局限性，包括对初始聚类中心的敏感性、簇的个数需要事先指定、对异常值较为敏感等。因此，在实际应用时需要根据数据的特点和需求进行适当的调整和优化。 本次实验使用sklearn库中的K-means算法对1999年全国31个省份的消费水平进行聚类。数据包含8个主要变量，包括食品、衣着、家庭设备用品及服务、医疗保健、交通和通讯、娱乐教育文化服务、居住以及杂项商品和服务。通过对这些变量进行聚类分析，可以了解各个省份之间在消费水平上的差异和相似性。 实验的技术路线是使用sklearn库中的K-means算法实现聚类分析。首先导入相关的库和数据，然后调用KMeans类进行聚类分析。在聚类的过程中，选择了适当的聚类中心数目，用于划分样本集合。聚类分析完成后，可以通过可视化的方式展示各个省份在消费水平上的聚类结果，进一步分析和解读数据。 通过K-means聚类分析，我们可以获得1999年全国31个省份的消费水平在国内的情况，从而为相关决策提供参考依据。此外，K-means算法还可以应用于其他领域，如推荐系统、图像处理和自然语言处理等。 总之，K-means聚类算法是一种常用的无监督学习算法，能够将数据集划分为具有相似特征的簇。通过实验和分析，我们可以利用K-means算法对数据进行聚类，实现对数据的分组和分类。在实际应用中，我们可以根据需求对算法进行调整和优化，以获得更好的聚类结果。