光纤中微Fabry-Perot干涉仪的飞秒激光加工研究

88 浏览量更新于2024-07-15 收藏 1.22MB PDF 举报

"探究微法布里-珀罗干涉仪在石英光纤中的应用及其制造方法" 这篇研究论文主要关注的是微法布里-珀罗干涉仪（MFPIs）在光纤中的制造及其在应变和温度传感中的特性。MFPIs是通过近红外飞秒激光在单模光纤（SMF）和光子晶体光纤（PCF）中加工而成的。飞秒激光是一种非常短脉冲的激光，能够在材料中实现精细的微结构加工，而不会引起大的热效应，因此非常适合用于制造精密的光学传感器。首先，作者比较了基于SMF和PCF的两种MFPIs的性能。它们都具有相同的腔体长度，但由于其不同的波导结构，PCF-MFPI的应变敏感性小于SMF-MFPI。这表明光纤的结构对其传感性能有显著影响。PCF的孔洞结构可能提供了不同的光传播路径，从而导致不同的应变响应。同时，两种MFPIs在温度传感方面的表现相近，这意味着它们在这方面的应用可能具有相似的潜力。 MFPIs作为光学传感器，其工作原理基于光的干涉现象。当外部物理量如应变或温度改变时，会改变光纤内光的传播路径长度，进而导致干涉图案的变化，从而可以被用来精确测量这些变化。这种特性使得MFPIs在光纤通信、环境监测、生物医学等领域有着广泛的应用。此外，虽然论文的摘要中并未详细提及，但在实际应用中，MFPIs的性能还受到许多因素的影响，如光纤的材料性质、腔体长度的精确控制、以及信号处理和解调技术等。优化这些参数对于提高传感器的灵敏度和稳定性至关重要。另一方面，摘要中提到的另一部分内容，即关于SDSS（ Sloan Digital Sky Survey）白矮星的质量和亮度函数以及形成率的研究，看似与主题不直接相关，可能是由于错误地包含了这部分信息。SDSS是一个大型天文观测项目，它收集了大量的白矮星光谱数据，这些数据对于研究白矮星的统计特性，如质量分布、形成速率和演化过程等，具有重要意义。然而，这部分内容与微法布里-珀罗干涉仪在光纤中的应用并无直接联系，因此在讨论MFPIs时可以忽略这部分信息。这篇论文的核心在于展示了如何利用飞秒激光在不同类型的光纤中制造MFPIs，并探讨了它们在应变和温度传感中的差异，强调了光纤结构对传感器性能的影响。这对于进一步优化光纤传感器的设计和提高其在实际应用中的性能具有指导意义。

4 Hu, Wu & Wu: DA white dwarfs in the SDSS

0.3 0.5 0.7 0.9 1.1

0.5

0.7

0.9

1.1

other

spec

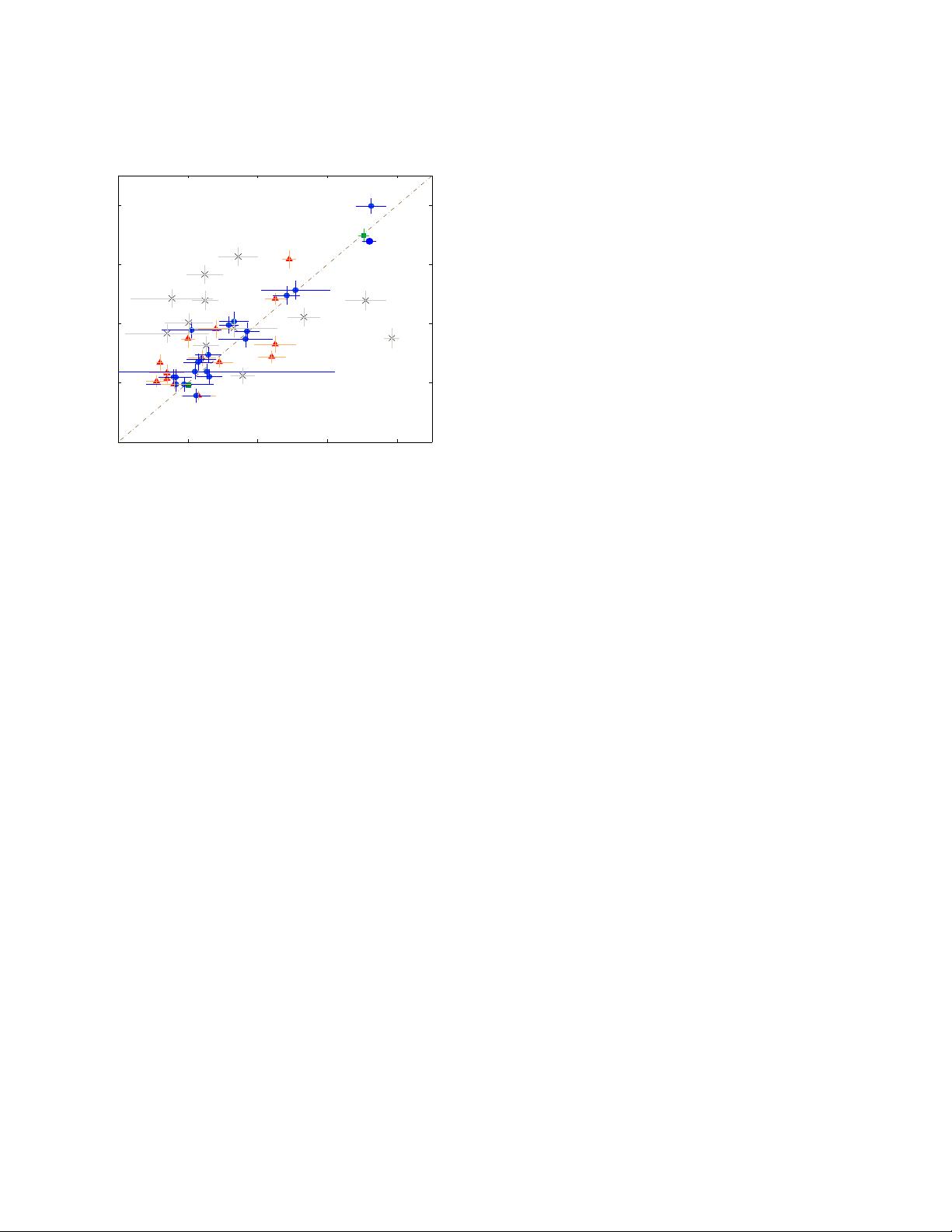
Fig. 2. A comparison between the WD mass derived from

the evolutionary model and those determined by other

methods without us ing a theoretical M-R relation. Both

axes are in unit of M

⊙

. All po ints in the diagram are

listed in Table 1. Triangles repre sent the WDs with mass

determined by the triangle parallaxes and surface grav-

ity. Circles represent WDs with mass determined by the

gravitational redshifts. Squares repres ent WDs with mass

derived from the orbital parameters. Crosses represents

WDs cooler than 12000K. The dashed line repre sents

spec

= M

other

are obviously larger. This is beca us e these cooler WDs are

likely to be convective. BSL have convincingly proved that

the convection eﬀect leads to signiﬁcant amounts of helium

(which is invisible in the spectra) entering the atmosphere,

producing higher pressure which would substantially af-

fect the s pectral line proﬁles. The total eﬀect on the spec-

tral line is indistinguishable from the increased surface

gravity. In other words, a low-tempera tur e DA WD with

large surfac e gravity might actually be a helium-rich star

with lower surface gravity (and correspondingly with lower

mass). So the scatter in the ma sses estimated with diﬀer-

ent methods for cooler WDs possibly has less to do with

the evolutionary model tha t we adopted but is mainly due

to the techniques o f analyzing the spectra l lines. For this

reason, we remove these WDs from our statistical a naly-

ses.

There are still some high-temperature WDs for which

the diﬀerent mass estimates do not match very well. A few

factors can contribute to this discrepancy, such as the tech-

niques of ﬁtting the spectral lines, the uncertainties of the

observational parameters. etc. One of the most important

factors is that there seems to be no appr opriate evolution-

ary model fo r these high-tempera tur e WDs. For example,

G238-4 4, GD140, EG50, and EG2 1 have re latively higher

sp e c troscopic mass compared with the mass derived from

other methods. If we apply a thin hydrogen layer model

(q(H) = −1, q(He) = −4) or a metal core (like F e core)

for these four WDs, their spe c troscopic mass will be lower

by 0 .04∼0.06 M

⊙

, and thus the mass comparison of these

four WDs would be better. Moreover, the presence of he-

lium in the atmosphere would also signiﬁcantly inﬂuence

the mass estimate. Boudreault & Bergero n (2005) gave

a detailed discussion of this eﬀect. They calculated the

masses by using the models of Fo ntaine et al. (2001) and

assuming a mixed composition in the atmosphere with

M(He)/M(H) = 1 rather than a pure hydrogen atmo-

sphere, and obtained similar results that the mea n M

spec

of WDs in their sample will be lower by 0.2 M

⊙

. Thus, if

we adjust the thickness of the envelope, the composition

of the atmosphere and the atom in the core, more than

half of the WDs in Fig. 2 will have their M

spec

equal to the

mass derived by the o ther method. Therefore, we may ﬁnd

the most appro priate e volutionary model for each WD by

matching two kinds of mass estimates, and then the dis-

crepancy in Fig. 2 would be alleviated.

However, for most DA WDs from SDSS DR1 in our

sample, we do not have paralla x or gravitational redshift

data to derive a second mass estimate and do not have fur-

ther information about their interna l structure and atmo-

spheric composition. So we will just ass ume a theoretically

appropriate model for our samples. From Fig . 2, we ﬁnd

that the comparison results are satisfactory in general, ig-

noring the low-temperature WDs. We then conclude that

the assumptions of evolutionary models we adopted are

generally reliable.

After testing the applicability of the model of Panei et

al. (2000), we use it to c alculate the masses of SDSS DA

WDs in our sample. From the T

eff

-log g diagram shown

in Fig. 1, we can see that using the two parameters T

eff

and log g we can determine the mass of the WDs (the the-

oretical lines can be interp olated to cover the area that

the lines do not cover in the ﬁgure). The other parame-

ters of the WDs also can be calc ulated based on the mass

estimation.

Using the methods described above, we can calcu-

late the radius R, luminosity L and bolometric mag-

nitude M

bol

for WDs. Similar to the determination of

mass, the cooling age of a WD can be der ived by in-

terpolating the grids of the evolutionary models, thus

log Age = log Age(T

eff

, log g). The bolometric cor rec-

tion (B.C.) in the g band can be obtained by using the

model atmospheres of Bergeron et al. (1995b). B.C . is de-

rived through interpolating the T

eff

and log g into the

grid of the model atmosphere in Bergeron et al. (1995b)

for the ugriz system, B.C. = B.C.

Bergeron

eff

, log g).

The distance r (in p c) of the star can be derived from the

B.C. and the relations hip between the absolute magnitude

and visual magnitude in the g band: M

bol

= M

+ B.C.

= g − 5 − 5 log r − A

, where A

is the extinction in

the g band which is provided by the SDSS.

To compare our re sults with other pr e vious work, we

also derived the absolute magnitude of WDs in the V band

which were commonly used in previous studies. Using the

results of B e rgeron et al. (1 995b), we ca n easily c onvert

剩余15页未读，继续阅读

weixin_38677648

粉丝: 5
资源: 886

光纤中微Fabry-Perot干涉仪的飞秒激光加工研究

基于MATLAB的光纤Fabry-Perot干涉仪光源光谱信号的仿真计算.pdf

网络游戏-使用Fabry-Perot光二极管自注入锁定的密集波分复用无源光网络系统.zip

掺铒光纤动态光栅与光纤Bragg光栅Fabry-Perot腔特性研究

fabry-perot 谐振腔天线

matlab 干涉光谱,基于MATLAB的光纤Fabry-Perot干涉仪光源光谱信号的仿真计算

法布里珀罗仿真matlab

optisystem半导体激光器

python与光学仿真

计算机仿真、分析法布里-珀罗干涉仪单色光、白光的干涉现象的代码

激光干涉位移检测法的测量原理

最新资源