二维图形变换：齐次坐标与基本变换

"二维图形变换原理介绍，涉及齐次坐标、基本变换类型如恒等变换、比例变换和镜像变换在机械CAD/CAM技术中的应用。" 在计算机图形学中，二维图形变换是图形处理的核心概念之一，它涉及到如何通过数学运算改变图形的位置、大小和形状。本内容主要讲解了二维图形变换的基本原理，包括点的表示、变换矩阵以及齐次坐标系统。 首先，点在二维空间中的表示通常使用直角坐标系 (X, Y) 来描述，也可以表示为矩阵形式 [x, y] 或 [x/y]。在图形变换中，这些点的位置向量是基础元素。 其次，变换矩阵是实现图形变换的关键工具。一个点 P 经过变换后成为点 P'，可以通过点 P 的位置向量与2×2的变换矩阵 T 相乘来得到。例如，新点 P' 的坐标可以用矩阵表达式 P' = TP 表示，其中 T 的元素 A, B, C, D 决定了变换的具体性质。 接着，引入了齐次坐标系统，这是一种扩展坐标表示法，使用 N+1 维向量表示 N 维向量。在二维空间中，点 (X, Y) 可以用 (X, Y, H) 来表示，H 是非零常量，通常取 H=1。这样，齐次坐标 (X, Y, 1) 能够包容笛卡尔坐标系中的点 (X, Y)。在齐次坐标下，原本的2×2变换矩阵扩展为3×3矩阵，以适应额外的坐标分量。 然后，讨论了三种基本的二维图形变换类型： 1. 恒等变换：保持点的位置不变，变换矩阵为单位矩阵，即所有对角线元素为1，非对角线元素为0，表示 x'=x, y'=y。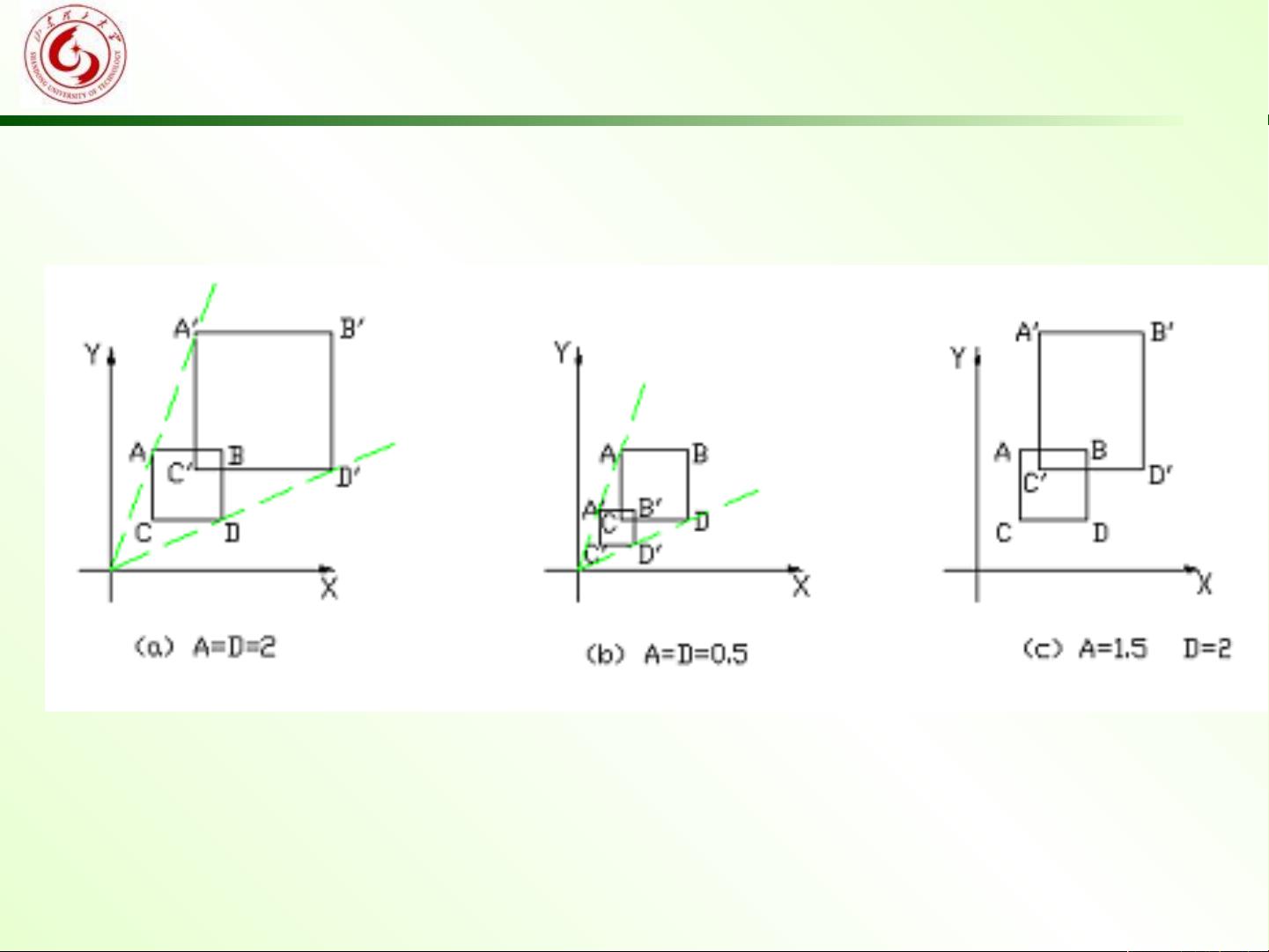 2. 比例变换：点按与原点的距离比例放大或缩小，变换矩阵形式为 [A, 0; 0, D]，其中 A 和 D 是比例因子。当 A 和 D 大于0且相等时，图形等比例放大或缩小；当 A 或 D 为负值时，图形会沿相应的轴翻转。 3. 镜像变换（对称反射变换）：当变换矩阵的某些元素为负值时，可以实现关于X轴、Y轴或原点的对称变换。例如，当 A=D=-1 时，点将关于原点对称。 这些基本变换类型是构建复杂图形变换的基础，它们可以组合使用，形成复合变换，以实现更丰富的图形操作。例如，通过组合比例变换和镜像变换，可以创建出各种对称图案和图形变形效果。在机械CAD/CAM技术中，这些变换被广泛应用于设计和模拟机械部件的运动、形状修改等方面，是计算机辅助设计不可或缺的一部分。