分支限界法详解:算法设计的关键技术
版权申诉
52 浏览量
更新于2024-07-04
收藏 1.18MB DOC 举报
第八章 "分支与限界法" 是算法设计与分析的重要章节,主要探讨如何通过合理利用分支策略和界限估计来优化搜索过程。本章的核心概念包括:
1. **分支与限界法的基本思想**:
- 该方法的关键在于在搜索过程中,每个节点评估其子节点可能达到的目标函数值(界),这些值被保存在优先队列或堆中,以便根据上界或下界进行决策。
- 搜索策略优先选择具有最大或最小界值的节点,确保探索最有潜力的解决方案区域。
- 当遇到叶子节点且其目标函数值等于已知的最优解时,该路径即为最优解,目标函数值即为问题的最大或最小值。
2. **目标函数的上下界**:
- 对于最小值问题,目标函数的下界表示搜索结果不会小于这些下界;对于最大值问题,上界则表示不会大于这些上界。
- 部分解通过边界条件限制了可能的最优解范围,有助于有效地剪枝,减少不必要的搜索。
3. **分支方法**:
- 有两种不同的分支策略:一是全分支,根据解向量的取值范围划分[pic]个子节点,可能导致较大的存储需求;二是二分分支,仅针对特定值进行分支,空间复杂度较低。
- 在完全[pic]叉树情况下,可以计算出更精确的存储空间需求。
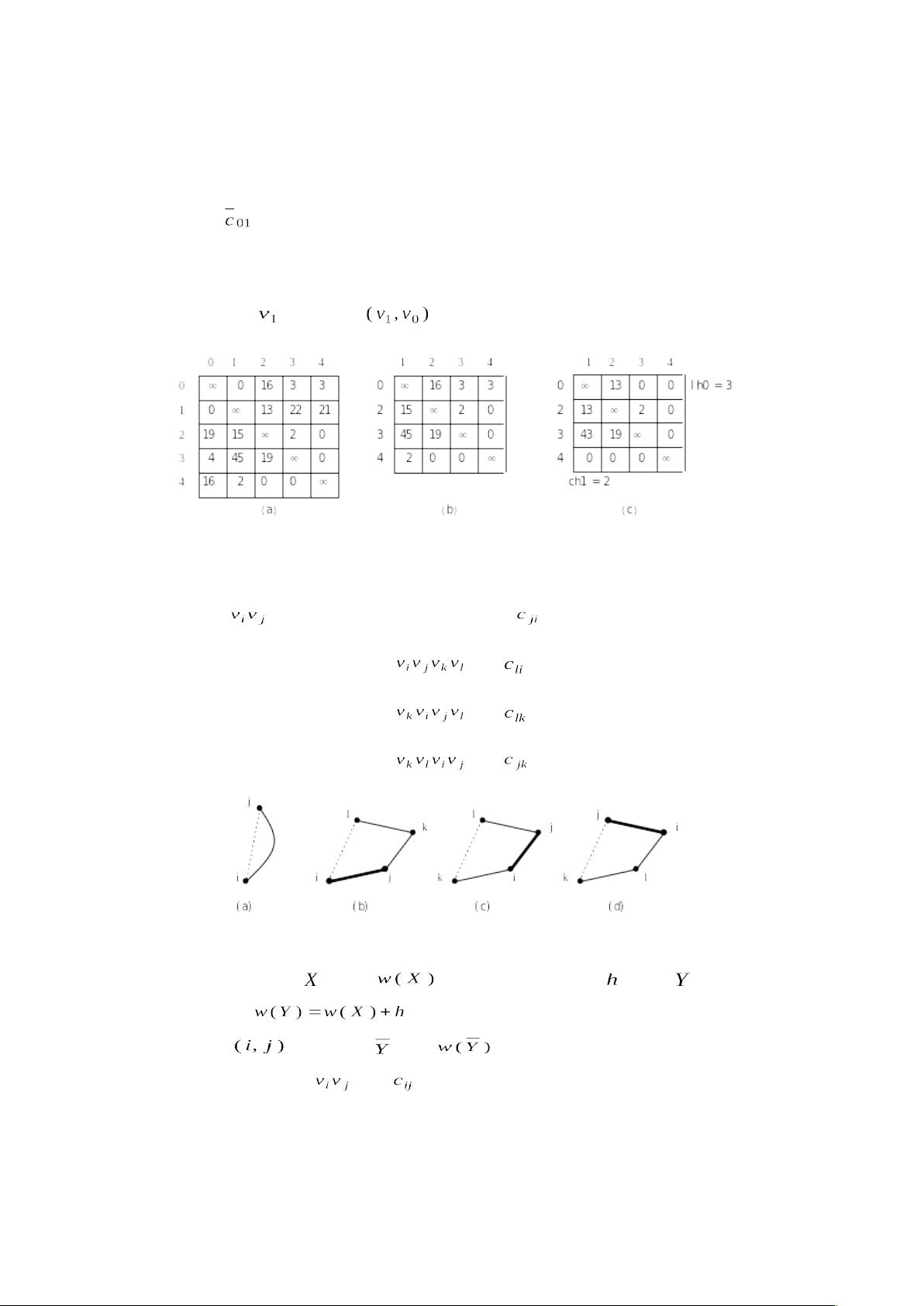
4. **货郎担问题与有向赋权图**:
- 货郎担问题涉及到寻找有向赋权图[pic]中的最短哈密尔顿回路,其中邻接矩阵[pic]表示顶点之间的边和费用关系。
- 费用矩阵的特性包括:矩阵中的[pic]元素代表从一个顶点到另一个顶点的边的费用,对于寻找最短路径至关重要。
- 哈密尔顿回路与费用矩阵紧密相关,证明了哈密尔顿回路中的边对应费用矩阵中的特定元素。
通过学习这一章节,学生将理解如何利用分支与限界法解决复杂问题,如路径规划和组合优化,并掌握如何在有限资源下找到最佳解。在实践中,这种方法广泛应用于旅行商问题、网络流问题和机器学习的搜索算法等领域。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2021-09-17 上传
2023-07-04 上传
2021-10-11 上传
2021-10-11 上传
老帽爬新坡
- 粉丝: 97
- 资源: 2万+
最新资源
- 海战小游戏.zip易语言项目例子源码下载
- windows 安装mariaDb 数据库操作指南 包含安装包文件
- aquamarine:带有mermade.js的rustdoc内联图
- 生活服务网站模版
- aframe-text-sprite:THREE.TextSprite的包装器
- HP_ruda:ゲートフォリオサイト自作ゲームなど
- 施工组织设计 (3).zip
- vbscript是什么,他的作用
- 解压缩并在PC和PPC上显示动画GIF
- 建筑设计院网站
- CSmusgen-开源
- 海洋黑白棋.zip易语言项目例子源码下载
- toolbox
- elasticsearch-guzzle5connection:提供异步连接 guzzle5
- A1_CS2AI
- campescassiano.github.io