没有合适的资源?快使用搜索试试~ 我知道了~
首页无线通信基础习题答案 Fundamentals.of.Wireless.Communication
资源详情
资源评论
资源推荐

Chapter 1
Solutions to Exercises
1

Chapter 2
Solutions to Exercises
Exercise 2.1. 1. Let r(t) =
p
r
2
0
+ (vt)
2
+ 2r
0
vt cos(φ). Then,
E
r
(f, t, r(t), θ, ψ)) =
<[α(θ, ψ, f) exp{j2πf(1 − r(t)/c)}]
r(t)
.
Moreover, if we assume that r
0
À vt, then we get that r(t) ≈ r
0
+ vt cos(φ).
Thus, the doppler shift is fv cos(φ)/c.
2. Let (x, y, z) be the position of the mobile in Cartesian coordinates, and (r, ψ, θ)
the position in polar coordinates. Then
(x, y, z) = (r sin θ cos ψ, r sin θ sin ψ, r cos θ)
(r, ψ, θ) =
³
p
x
2
+ y
2
+ z
2
, arctan(y/x), arccos(z/
p
x
2
+ y
2
+ z
2
)
´
˙
ψ =
x ˙y − ˙xy
x
2
+ y
2
˙
θ = −
˙zr − z ˙r
r
2
p
1 − (z/r)
2
We see that
˙
ψ is small for large x
2
+ y
2
. Also
˙
θ is small for |z/r| < 1 and r large.
If |r/z| = 1 then θ = 0 or θ = π and v <= r|
˙
θ| so v/r large assures that
˙
θ is
small. If r is not very large then the variation of θ and ψ may not be negligible
within the time scale of interest even for moderate speeds v. Here large depends
on the time scale of interest.
Exercise 2.2.
E
r
(f, t) =
α cos [2πf (t − r(t)/c)]
2d − r(t)
+
2α [d − r(t)] cos [2πf (t − r(t)/c)]
r(t)[2d − r(t)]
−
α cos [2πf (t + (r(t) − 2d)/c)]
2d − r(t)
2

Tse and Viswanath: Fundamentals of Wireless Communication 3
=
2α sin [2πf (t − d/c)] sin [2πf (r(t) − d) /c]
2d − r(t)
+
2α [d − r(t)] cos [2πf (t − r(t)/c)]
r(t)[2d − r(t)]
(2.1)
where we applied the identity
cos x − cos y = 2 sin
µ
x + y
2
¶
sin
µ
y − x
2
¶
We observe that the first term of (2.1) is similar in form to equation (2.13) in the
notes. The second term of (2.1) goes to 0 as r(t) → d and is due to the difference in
propagation losses in the 2 paths.
Exercise 2.3. If the wall is on the other side, both components arrive at the mobile
from the left and experience the same Doppler shift.
E
r
(f, t) =
<[α exp{j2π[f(1 − v/c)t − fr
0
/c]}]
r
0
+ vt
−
<[α exp{j2π[f(1 − v/c)t − f(r
0
+ 2d)/c]}]
r
0
+ 2d + vt
We have the interaction of 2 sinusoidal waves of the same frequency and different
amplitude.
Over time, we observe the composition of these 2 waves into a single sinusoidal
signal of frequency f (1−v/c ) and constant amplitude that depends on the attenuations
(r
0
+ vt) and (r
0
+ 2d + vt) and also on the phase difference f2d/c.
Over frequency, we observe that when f2d/c is an integer both waves interfere
destructively resulting in a small received signal. When f2d/c = (2k + 1)/2, k ∈ Z
these waves interfere constructively resulting in a larger received signal. So when f
is varied by c/4d the amplitude of the received signal varies from a minimum to a
maximum.
The variation over frequency is similar in nature to that of section 2.1.3, but since
the delay spread is different the coherence bandwidth is also different.
However there is no variation over time because the Doppler spread is zero.
Exercise 2.4. 1. i) With the given information we can compute the Doppler spread:
D
s
= |f
1
− f
2
| =
fv
c
|cos θ
1
− cos θ
2
|
from which we can compute the coherence time
T
c
=
1
4D
s
=
c
4fv|cos θ
1
− cos θ
2
|
ii) There is not enough information to compute the coherence bandwidth, as it
depends on the delay spread which is not given. We would need to know the
difference in path length to compute the delay spread T
d
and use it to compute
W
c
.

Tse and Viswanath: Fundamentals of Wireless Communication 4
2. From part 1 we see that a larger angular range results in larger delay spread and
smaller coherence time. Then, in the richly scattered environment the channel
would show a smaller coherence time than in the environment where the reflectors
are clustered in a small angular range.
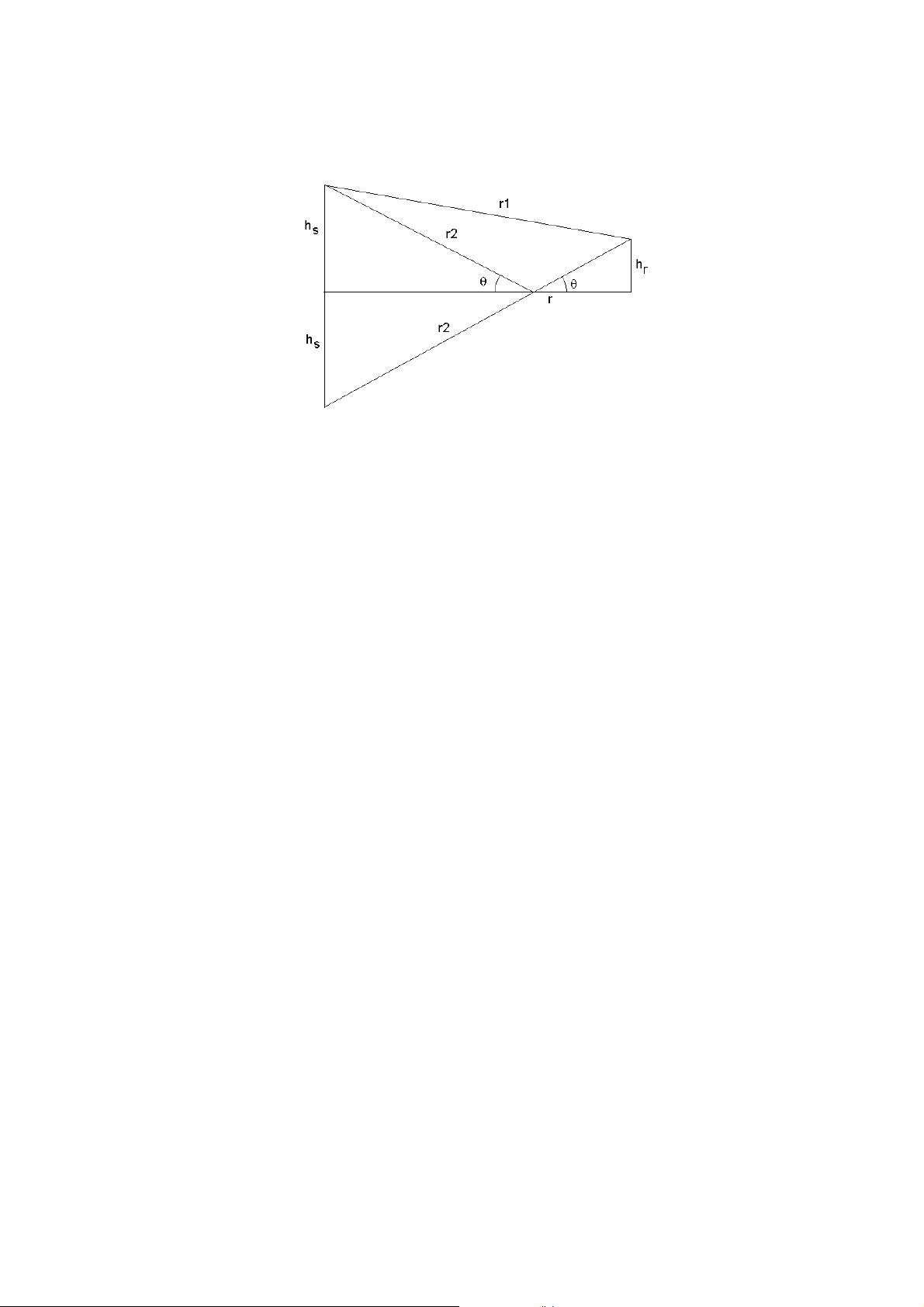
Exercise 2.5. 1.
r
1
=
p
r
2
+ (h
s
− h
r
)
2
= r
p
1 + (h
s
− h
r
)
2
/r
2
≈ r(1 +
(h
s
− h
r
)
2
2r
2
)
r
2
=
p
r
2
+ (h
s
+ h
r
)
2
= r
p
1 + (h
s
+ h
r
)
2
/r
2
≈ r(1 +
(h
s
+ h
r
)
2
2r
2
)
r
2
− r
1
≈
(h
s
+ h
r
)
2
− (h
s
− h
r
)
2
2r
=
h
2
s
+ h
2
r
+ 2h
s
h
r
− h
2
s
− h
2
r
+ 2h
s
h
r
2r
=
2h
s
h
r
r
Therefore b = 2h
s
h
r
.
2.
E
r
(f, t) ≈
Re[α[exp{j2π(ft − fr
1
/c)] − exp{j2π(ft − fr
2
/c)]]
r
1
=
Re[α[exp{j2π(ft − fr
1
/c)][1 − exp(j2πf(r
1
− r
2
)/c)]
r
1
≈
Re[α[exp{j2π(ft − fr
1
/c)][1 − exp(j2πf/c ∗ b/r)]
r
1
≈
Re[α[exp{j2π(ft − fr
1
/c)][1 − (1 − j2πf/c ∗b/r)]
r
1
=
2πf|α|b
cr
2
<[j exp(j∠α) exp[j2π(ft −f r
1
/c)]]
= −
2πf|α|b
cr
2
sin[2π(ft − fr
1
/c) + ∠α]]
Therefore β = 2πf|α|b/c.
3.
1
r
2
=
1
r
1
+ (r
2
− r
1
)
=
1
r
1
[1 + (r
2
− r
1
)/r
1
]
≈
1
r
1
µ
1 −
r
2
− r
1
r
1
¶
≈
1
r
1
µ
1 −
b
r
2
1
¶
Therefore if we don’t make the approximation of b) we get another term in
the expansion that decays as r
−3
. This term is negligible for large enough r as
compared to β/r
2
.
Tse and Viswanath: Fundamentals of Wireless Communication 5
Exercise 2.6. 1. Let f
2
be the probability density of the distance from the origin
at which the photon is absorbed by exactly the 2nd obstacle that it hits. Let x
be the location of the first obstacle, then
f
2
(r) = P {photon absorbed by 2nd obstacle at r}
=
Z
x
P {absorbed by 2nd obstacle at r | not absorbed by 1st obstacle at x}
× P {not absorbed by 1st obstacle at x} dx
Since the obstacle are distributed according to poisson process which has mem-
oryless distances between consecutive points, the first term inside the integral is
f
1
(r − x). The second term is the probability that the first obstacle is at x and
the photon is not absorbed by it. Thus, it is given by (1 − γ)q(x). Thus,
f
2
(r) =
Z
∞
x=−∞
(1 − γ)q(x)f
1
(r − x)dx
2. Similarly, we observe that f
k+1
(r) is given by
f
k+1
(r) =
Z
x
P {absorbed by (k + 1)th obst at r | not absorbed by 1st obst at x}
× P {not absorbed by 1st obstacle at x} dx
=
Z
∞
x=−∞
(1 − γ)q(x)f
k
(r − x)dx (2.2)
3. Summing up (2.2) for k = 1 to ∞, we get:
∞
X
k=2
f
k
(r) =
Z
∞
x=−∞
(1 − γ)q(x)
Ã
∞
X
k=1
f
k
(r − x)
!
dx
剩余132页未读,继续阅读
Rachel思密达
- 粉丝: 0
- 资源: 4
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- RTL8188FU-Linux-v5.7.4.2-36687.20200602.tar(20765).gz
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
- SPC统计方法基础知识.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0