没有合适的资源?快使用搜索试试~ 我知道了~
首页《随机过程及其在金融的应用》习题五答案.pdf
资源详情
资源评论
资源推荐

第
5
章
1. 对 Markov 链,
,试证条件
,
,
等价于对所有时刻 n
,
m 及所有状态
,,
,
,,
有
,
,,
,
,
解:证明:
,
,,
,
,,
,
,
,,
,,
,,
,,
,
,
由
(1)
得到:
,,
,,
,,
,,
,
,
,,
,
,
,
,
在 中取 ,即
2. 考虑状态 0,1,2 上的一个 Markov 链
,它有转移概率矩阵 ,
初始分布为
0 1 2
0.4 0.4 0.2p p p , ,
。试求概率
0 1 2
P( 0 1 2)X X X , ,
。
0 1 2 2 1 1 0 0
01 12
0 1 2
P 0 1 2 P( 2 | 1)P( 1| 0)P( 0)
0.1 0
P 0 1 2 0 0.1 0.4 0
X X X X X X X X
p p
X X X
解: , ,
转移概率矩阵可得: ,
所以 , ,
3.
从
中,等可能地取出
个数,取后放回,连续去下去,若在前
n
次所取得的最大数为
j
,就说“质
点”在第
n
步处于状态
j
,该“质点”运动构成一个
链,试求一步转移概率矩阵。
解:下面记
为矩阵中第 i 行,第 j 列元素
1, 1i j
表示直到第
步最大数是
,第
步也是
概率为
……
的概率也是
所以
…
如此类推
而当
时
,
可知一步转移矩阵是上三角矩阵
,
对角线上元素分别为
1 2
, , ,1
6 6
,右上方元素
全是
1
6
。
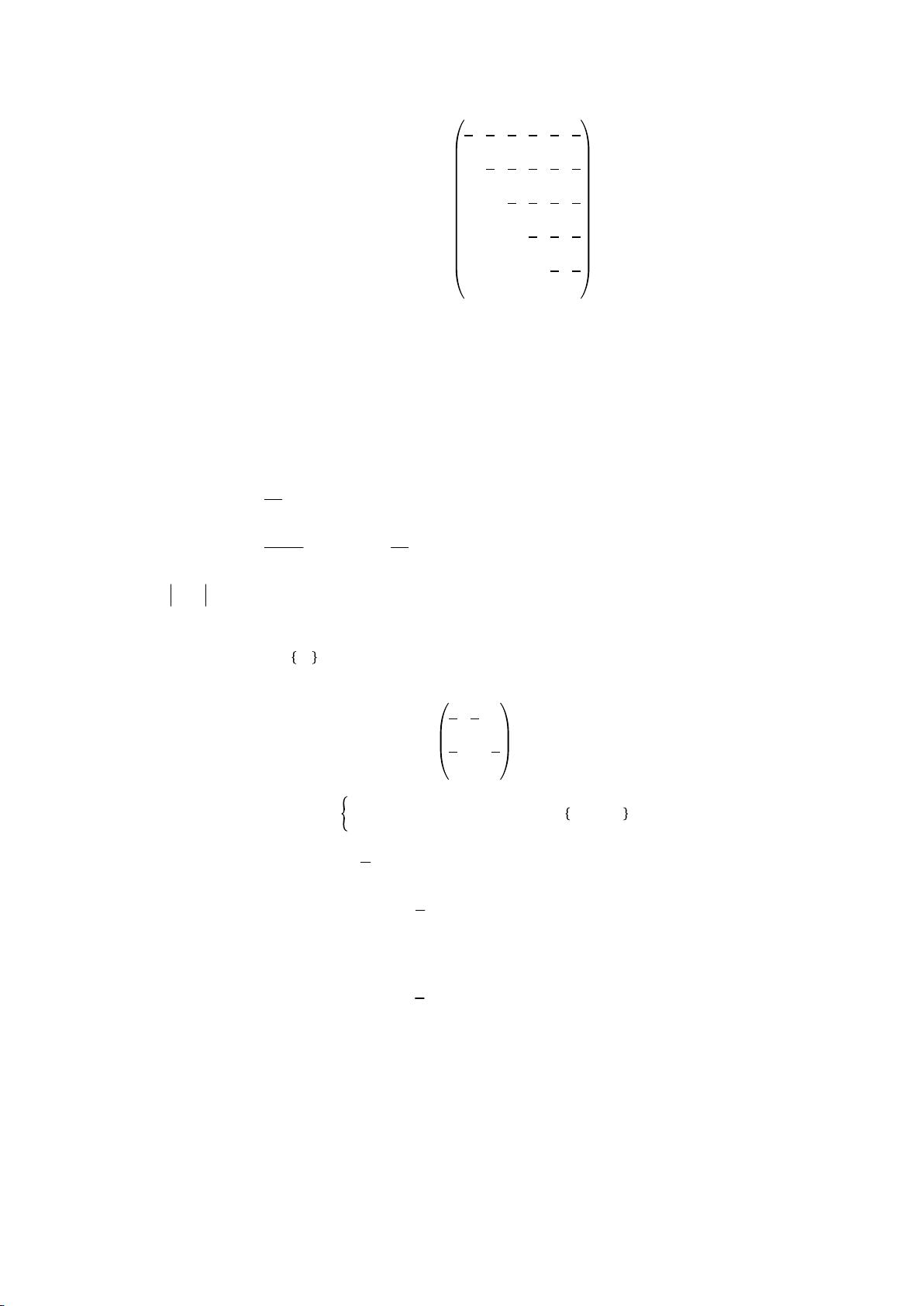
概率转移矩阵
4.
(
1
)
A
,
B
两罐总共装着
N
个球,在时刻
n
先从
N
个球中等概率地任取一球;然后从
A
,
B
两罐中任选
一个,选中
A
的概率为
p
,选中
B
的概率为
1-p
;之后再将选出的球放入选好的罐中。设
为每次试验时
A
罐中的球数,试求次
Markov
链的转移概率矩阵。
(
2
)重复投掷一枚质地均匀的硬币直到连续出现两次正面为止,试引入以连续出现次数为状态空间的
Markov
链,并求出平均需要掷多少次实验才可以结束。
解:
(
1
)
1
1
ii
p ip N i p
N
, 1i i
N i
p p
N
,
, 1
1
i i
i
p p
N
当
1i j
时,
0
ij
p
。
(
2
)用
表示第
n
次掷币时连续出现两次正面的次数,掷出反面的次数为
0
,显然,当给定
时,
与
,,
无关,故
为 Markov 链,且为时齐的。因为只要没有掷出两次正面,过程都与时刻 n 无
关,一般转移概率阵
第
次出现正面
第
次出现反面
,
1 2
1
P N 2 P 1 2
4
X X ,
3 2 1
1
P N 3 P 2 1 0
8
X X X , ,
4 3 2 1 4 3 2 1
4 3 2
P N 4 P 2 1 0 0 P 2 1 0 1
1
P 2 1 0
8
X X X X X X X X
X X X
, , , , , ,
, ,

5 4 3 2 1
5 4 3 2 1
5 4 3 2 1
5 4 3 2 5 4 3 2 1
5
P N 5 P 2 1 0 0 0
P 2 1 0 0 1
P 2 1 0 1 0
P 2 1 0 0 P 2 1 0 1 0
P 2 |
X X X X X
X X X X X
X X X X X
X X X X X X X X X
X
, , , ,
, , , ,
, , , ,
, , , , , , ,
4 4 3 3 2 2
5 4 4 3 3 2 2 1 1
5
1)P 1| 0 P 0| 0 P( 0
P 2| 1 P 1| 0 P 0| 1 P 1| 0 P 0
1 1 1
16 32 2
X X X X X X
X X X X X X X X X
6 5 4 3 2 1 6 5 4 3 2 1
6 5 4 3 2 1 6 5 4 3 2 1
6 5 4 3 2 1
P N 6 P 2 1 0 0 0 0 P 2 1 0 0 0 1
P 2 1 0 0 1 0 P 2 1 0 1 0 0
P 2 1 0 1 0 1
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X
, , , , , , , , , ,
, , , , , , , , , ,
, , , , ,
6 5 4 3 2 6 5 4 3 2 1
6 5 4 3 2 6 5 4 3 2 1
6 5 4 3 2
P 2 1 0 0 0 P 2 1 0 0 1 0
P 2 1 0 0 0 P 2 1 0 0 1 0
P 2 1 0 1 0
1 1
2
32
X X X X X X X X X X X
X X X X X X X X X X X
X X X X X
, , , , , , , , ,
, , , , , , , , ,
, , , ,
6
5
64 2
3 5
1 1 1 3
E N 2 3 4 5
4 8 2 2
平均需要掷
6
次实验才可以结束
5.
设
Markov
链
有状态
1,2,3
和一步转移概率矩阵
已知
,即初始分布矩阵为
,
。试求
(
1
)三步转移概率矩阵。
(
2
)经三步转移以后处于状态
2
的概率。
解:(
1
)
(2)初始分布矩阵为
,
时,
经三步转移以后处于状态
2
的概率为
0.375
6. 记
( 1, 2, )
i
Z i
为一串独立同分布的离散随机变量,
1
0
{ } 0( 0,1, 2, ), 1
k k
i
P Z k p k p
剩余12页未读,继续阅读
weixin_40787114
- 粉丝: 0
- 资源: 3
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- zigbee-cluster-library-specification
- JSBSim Reference Manual
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论1