没有合适的资源?快使用搜索试试~ 我知道了~
首页Squeeze-and-Excitation Networks
Squeeze-and-Excitation Networks
需积分: 0 11 下载量 155 浏览量
更新于2023-05-13
收藏 2.08MB PDF 举报
Squeeze-and-Excitation Networks的论文,不算比较经典的网络。需要学习,是对其他网络的改进版
资源详情
资源推荐

1
Squeeze-and-Excitation Networks
Jie Hu
[0000−0002−5150−1003]
Li Shen
[0000−0002−2283−4976]
Samuel Albanie
[0000−0001−9736−5134]
Gang Sun
[0000−0001−6913−6799]
Enhua Wu
[0000−0002−2174−1428]
Abstract—The central building block of convolutional neural networks (CNNs) is the convolution operator, which enables networks to
construct informative features by fusing both spatial and channel-wise information within local receptive fields at each layer. A broad
range of prior research has investigated the spatial component of this relationship, seeking to strengthen the representational power of
a CNN by enhancing the quality of spatial encodings throughout its feature hierarchy. In this work, we focus instead on the channel
relationship and propose a novel architectural unit, which we term the “Squeeze-and-Excitation” (SE) block, that adaptively recalibrates
channel-wise feature responses by explicitly modelling interdependencies between channels. We show that these blocks can be
stacked together to form SENet architectures that generalise extremely effectively across different datasets. We further demonstrate
that SE blocks bring significant improvements in performance for existing state-of-the-art CNNs at slight additional computational cost.
Squeeze-and-Excitation Networks formed the foundation of our ILSVRC 2017 classification submission which won first place and
reduced the top-5 error to 2.251%, surpassing the winning entry of 2016 by a relative improvement of ∼25%. Models and code are
available at https://github.com/hujie-frank/SENet.
Index Terms—Squeeze-and-Excitation, Image representations, Attention, Convolutional Neural Networks.
F
1 INTRODUCTION
C
ONVOLUTIONAL neural networks (CNNs) have proven
to be useful models for tackling a wide range of visual
tasks [1], [2], [3], [4]. At each convolutional layer in the net-
work, a collection of filters expresses neighbourhood spatial
connectivity patterns along input channels—fusing spatial
and channel-wise information together within local recep-
tive fields. By interleaving a series of convolutional layers
with non-linear activation functions and downsampling op-
erators, CNNs are able to produce image representations
that capture hierarchical patterns and attain global theo-
retical receptive fields. A central theme of computer vision
research is the search for more powerful representations that
capture only those properties of an image that are most
salient for a given task, enabling improved performance.
As a widely-used family of models for vision tasks, the
development of new neural network architecture designs
now represents a key frontier in this search. Recent research
has shown that the representations produced by CNNs can
be strengthened by integrating learning mechanisms into
the network that help capture spatial correlations between
features. One such approach, popularised by the Inception
family of architectures [5], [6], incorporates multi-scale pro-
cesses into network modules to achieve improved perfor-
• Jie Hu and Enhua Wu are with the State Key Laboratory of Computer
Science, Institute of Software, Chinese Academy of Sciences, Beijing,
100190, China.
They are also with the University of Chinese Academy of Sciences, Beijing,
100049, China.
Jie Hu is also with Momenta and Enhua Wu is also with the Faculty of
Science and Technology & AI Center at University of Macau.
E-mail: hujie@ios.ac.cn ehwu@umac.mo
• Gang Sun is with LIAMA-NLPR at the Institute of Automation, Chinese
Academy of Sciences. He is also with Momenta.
E-mail: sungang@momenta.ai
• Li Shen and Samuel Albanie are with the Visual Geometry Group at the
University of Oxford.
E-mail: {lishen,albanie}@robots.ox.ac.uk
mance. Further work has sought to better model spatial
dependencies [7], [8] and incorporate spatial attention into
the structure of the network [9].
In this paper, we investigate a different aspect of network
design - the relationship between channels. We introduce
a new architectural unit, which we term the Squeeze-and-
Excitation (SE) block, with the goal of improving the quality
of representations produced by a network by explicitly mod-
elling the interdependencies between the channels of its con-
volutional features. To this end, we propose a mechanism
that allows the network to perform feature recalibration,
through which it can learn to use global information to
selectively emphasise informative features and suppress less
useful ones.
The structure of the SE building block is depicted in
Fig. 1. For any given transformation F
tr
mapping the
input X to the feature maps U where U ∈ R
H×W ×C
,
e.g. a convolution, we can construct a corresponding SE
block to perform feature recalibration. The features U are
first passed through a squeeze operation, which produces a
channel descriptor by aggregating feature maps across their
spatial dimensions (H × W ). The function of this descriptor
is to produce an embedding of the global distribution of
channel-wise feature responses, allowing information from
the global receptive field of the network to be used by
all its layers. The aggregation is followed by an excitation
operation, which takes the form of a simple self-gating
mechanism that takes the embedding as input and pro-
duces a collection of per-channel modulation weights. These
weights are applied to the feature maps U to generate
the output of the SE block which can be fed directly into
subsequent layers of the network.
It is possible to construct an SE network (SENet) by
simply stacking a collection of SE blocks. Moreover, these
SE blocks can also be used as a drop-in replacement for the
original block at a range of depths in the network architec-
arXiv:1709.01507v4 [cs.CV] 16 May 2019
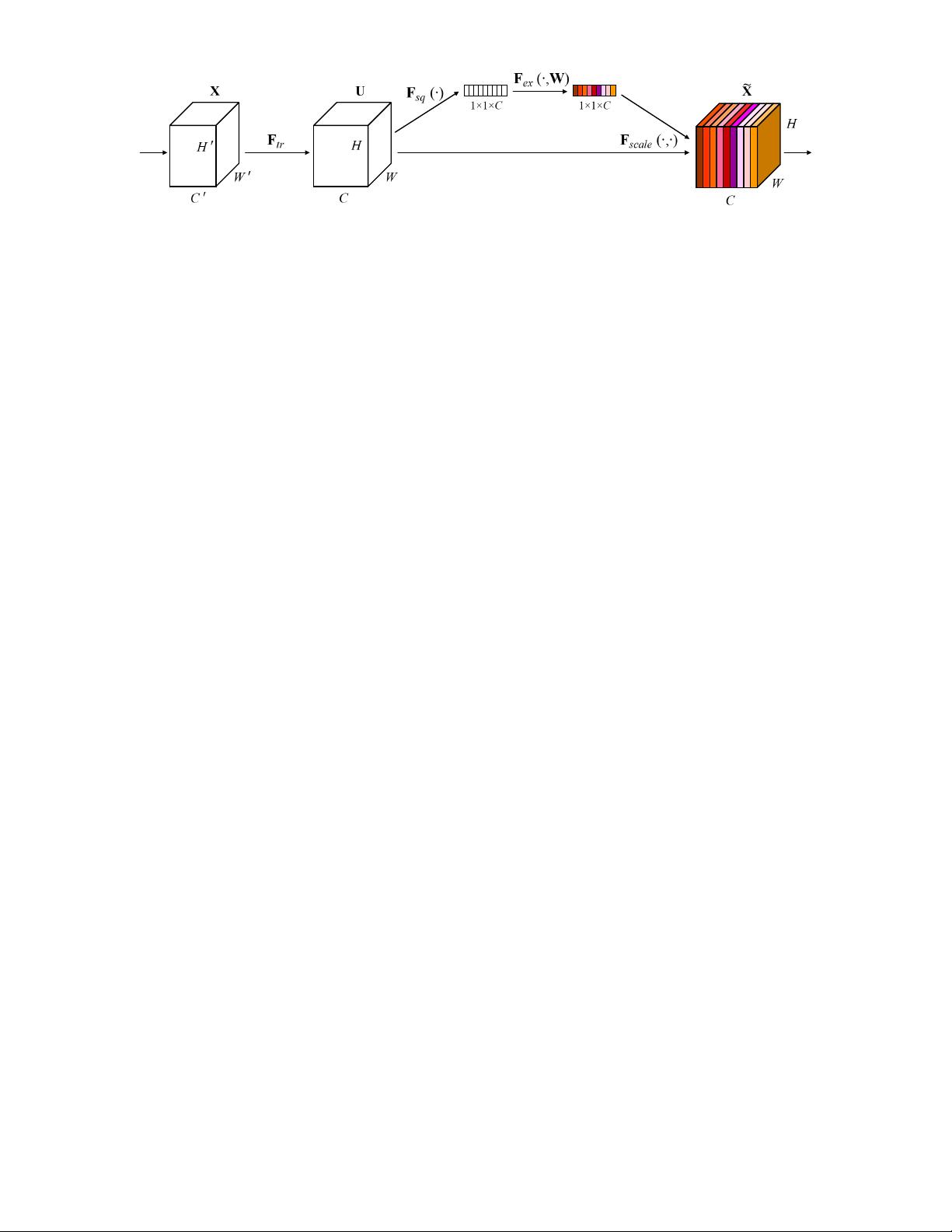
2
Fig. 1. A Squeeze-and-Excitation block.
ture (Section 6.4). While the template for the building block
is generic, the role it performs at different depths differs
throughout the network. In earlier layers, it excites infor-
mative features in a class-agnostic manner, strengthening
the shared low-level representations. In later layers, the SE
blocks become increasingly specialised, and respond to dif-
ferent inputs in a highly class-specific manner (Section 7.2).
As a consequence, the benefits of the feature recalibration
performed by SE blocks can be accumulated through the
network.
The design and development of new CNN architectures
is a difficult engineering task, typically requiring the se-
lection of many new hyperparameters and layer configura-
tions. By contrast, the structure of the SE block is simple and
can be used directly in existing state-of-the-art architectures
by replacing components with their SE counterparts, where
the performance can be effectively enhanced. SE blocks are
also computationally lightweight and impose only a slight
increase in model complexity and computational burden.
To provide evidence for these claims, we develop several
SENets and conduct an extensive evaluation on the Ima-
geNet dataset [10]. We also present results beyond ImageNet
that indicate that the benefits of our approach are not
restricted to a specific dataset or task. By making use of
SENets, we ranked first in the ILSVRC 2017 classification
competition. Our best model ensemble achieves a 2.251%
top-5 error on the test set
1
. This represents roughly a 25%
relative improvement when compared to the winner entry
of the previous year (top-5 error of 2.991%).
2 RELATED WORK
Deeper architectures. VGGNets [11] and Inception mod-
els [5] showed that increasing the depth of a network could
significantly increase the quality of representations that
it was capable of learning. By regulating the distribution
of the inputs to each layer, Batch Normalization (BN) [6]
added stability to the learning process in deep networks
and produced smoother optimisation surfaces [12]. Building
on these works, ResNets demonstrated that it was pos-
sible to learn considerably deeper and stronger networks
through the use of identity-based skip connections [13], [14].
Highway networks [15] introduced a gating mechanism to
regulate the flow of information along shortcut connections.
Following these works, there have been further reformula-
tions of the connections between network layers [16], [17],
1. http://image-net.org/challenges/LSVRC/2017/results
which show promising improvements to the learning and
representational properties of deep networks.
An alternative, but closely related line of research has
focused on methods to improve the functional form of
the computational elements contained within a network.
Grouped convolutions have proven to be a popular ap-
proach for increasing the cardinality of learned transforma-
tions [18], [19]. More flexible compositions of operators can
be achieved with multi-branch convolutions [5], [6], [20],
[21], which can be viewed as a natural extension of the
grouping operator. In prior work, cross-channel correlations
are typically mapped as new combinations of features, ei-
ther independently of spatial structure [22], [23] or jointly
by using standard convolutional filters [24] with 1 × 1
convolutions. Much of this research has concentrated on the
objective of reducing model and computational complexity,
reflecting an assumption that channel relationships can be
formulated as a composition of instance-agnostic functions
with local receptive fields. In contrast, we claim that provid-
ing the unit with a mechanism to explicitly model dynamic,
non-linear dependencies between channels using global in-
formation can ease the learning process, and significantly
enhance the representational power of the network.
Algorithmic Architecture Search. Alongside the works
described above, there is also a rich history of research
that aims to forgo manual architecture design and instead
seeks to learn the structure of the network automatically.
Much of the early work in this domain was conducted in
the neuro-evolution community, which established methods
for searching across network topologies with evolutionary
methods [25], [26]. While often computationally demand-
ing, evolutionary search has had notable successes which
include finding good memory cells for sequence models
[27], [28] and learning sophisticated architectures for large-
scale image classification [29], [30], [31]. With the goal of re-
ducing the computational burden of these methods, efficient
alternatives to this approach have been proposed based on
Lamarckian inheritance [32] and differentiable architecture
search [33].
By formulating architecture search as hyperparameter
optimisation, random search [34] and other more sophis-
ticated model-based optimisation techniques [35], [36] can
also be used to tackle the problem. Topology selection
as a path through a fabric of possible designs [37] and
direct architecture prediction [38], [39] have been proposed
as additional viable architecture search tools. Particularly
strong results have been achieved with techniques from
reinforcement learning [40], [41], [42], [43], [44]. SE blocks

3
can be used as atomic building blocks for these search
algorithms, and were demonstrated to be highly effective
in this capacity in concurrent work [45].
Attention and gating mechanisms. Attention can be in-
terpreted as a means of biasing the allocation of available
computational resources towards the most informative com-
ponents of a signal [46], [47], [48], [49], [50], [51]. Attention
mechanisms have demonstrated their utility across many
tasks including sequence learning [52], [53], localisation
and understanding in images [9], [54], image captioning
[55], [56] and lip reading [57]. In these applications, it
can be incorporated as an operator following one or more
layers representing higher-level abstractions for adaptation
between modalities. Some works provide interesting studies
into the combined use of spatial and channel attention [58],
[59]. Wang et al. [58] introduced a powerful trunk-and-mask
attention mechanism based on hourglass modules [8] that is
inserted between the intermediate stages of deep residual
networks. By contrast, our proposed SE block comprises a
lightweight gating mechanism which focuses on enhancing
the representational power of the network by modelling
channel-wise relationships in a computationally efficient
manner.
3 SQUEEZE-AND-EXCITATION BLOCKS
A Squeeze-and-Excitation block is a computational unit
which can be built upon a transformation F
tr
mapping an
input X ∈ R
H
0
×W
0
×C
0
to feature maps U ∈ R
H×W ×C
.
In the notation that follows we take F
tr
to be a convo-
lutional operator and use V = [v
1
, v
2
, . . . , v
C
] to denote
the learned set of filter kernels, where v
c
refers to the
parameters of the c-th filter. We can then write the outputs
as U = [u
1
, u
2
, . . . , u
C
], where
u
c
= v
c
∗ X =
C
0
X
s=1
v
s
c
∗ x
s
. (1)
Here ∗ denotes convolution, v
c
= [v
1
c
, v
2
c
, . . . , v
C
0
c
], X =
[x
1
, x
2
, . . . , x
C
0
] and u
c
∈ R
H×W
. v
s
c
is a 2D spatial kernel
representing a single channel of v
c
that acts on the corre-
sponding channel of X. To simplify the notation, bias terms
are omitted. Since the output is produced by a summation
through all channels, channel dependencies are implicitly
embedded in v
c
, but are entangled with the local spatial
correlation captured by the filters. The channel relationships
modelled by convolution are inherently implicit and local
(except the ones at top-most layers). We expect the learning
of convolutional features to be enhanced by explicitly mod-
elling channel interdependencies, so that the network is able
to increase its sensitivity to informative features which can
be exploited by subsequent transformations. Consequently,
we would like to provide it with access to global information
and recalibrate filter responses in two steps, squeeze and
excitation, before they are fed into the next transformation.
A diagram illustrating the structure of an SE block is shown
in Fig. 1.
3.1 Squeeze: Global Information Embedding
In order to tackle the issue of exploiting channel depen-
dencies, we first consider the signal to each channel in the
output features. Each of the learned filters operates with
a local receptive field and consequently each unit of the
transformation output U is unable to exploit contextual
information outside of this region.
To mitigate this problem, we propose to squeeze global
spatial information into a channel descriptor. This is
achieved by using global average pooling to generate
channel-wise statistics. Formally, a statistic z ∈ R
C
is gener-
ated by shrinking U through its spatial dimensions H × W ,
such that the c-th element of z is calculated by:
z
c
= F
sq
(u
c
) =
1
H × W
H
X
i=1
W
X
j=1
u
c
(i, j). (2)
Discussion. The output of the transformation U can be
interpreted as a collection of the local descriptors whose
statistics are expressive for the whole image. Exploiting
such information is prevalent in prior feature engineering
work [60], [61], [62]. We opt for the simplest aggregation
technique, global average pooling, noting that more sophis-
ticated strategies could be employed here as well.
3.2 Excitation: Adaptive Recalibration
To make use of the information aggregated in the squeeze
operation, we follow it with a second operation which aims
to fully capture channel-wise dependencies. To fulfil this
objective, the function must meet two criteria: first, it must
be flexible (in particular, it must be capable of learning
a nonlinear interaction between channels) and second, it
must learn a non-mutually-exclusive relationship since we
would like to ensure that multiple channels are allowed to
be emphasised (rather than enforcing a one-hot activation).
To meet these criteria, we opt to employ a simple gating
mechanism with a sigmoid activation:
s = F
ex
(z, W) = σ(g(z, W)) = σ(W
2
δ(W
1
z)), (3)
where δ refers to the ReLU [63] function, W
1
∈ R
C
r
×C
and
W
2
∈ R
C×
C
r
. To limit model complexity and aid general-
isation, we parameterise the gating mechanism by forming
a bottleneck with two fully-connected (FC) layers around
the non-linearity, i.e. a dimensionality-reduction layer with
reduction ratio r (this parameter choice is discussed in Sec-
tion 6.1), a ReLU and then a dimensionality-increasing layer
returning to the channel dimension of the transformation
output U. The final output of the block is obtained by
rescaling U with the activations s:
e
x
c
= F
scale
(u
c
, s
c
) = s
c
u
c
, (4)
where
e
X = [
e
x
1
,
e
x
2
, . . . ,
e
x
C
] and F
scale
(u
c
, s
c
) refers to
channel-wise multiplication between the scalar s
c
and the
feature map u
c
∈ R
H×W
.
Discussion. The excitation operator maps the input-
specific descriptor z to a set of channel weights. In this
regard, SE blocks intrinsically introduce dynamics condi-
tioned on the input, which can be regarded as a self-
attention function on channels whose relationships are not
confined to the local receptive field the convolutional filters
are responsive to.
剩余12页未读,继续阅读
颐水风华
- 粉丝: 9840
- 资源: 15
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- 利用迪杰斯特拉算法的全国交通咨询系统设计与实现
- 全国交通咨询系统C++实现源码解析
- DFT与FFT应用:信号频谱分析实验
- MATLAB图论算法实现:最小费用最大流
- MATLAB常用命令完全指南
- 共创智慧灯杆数据运营公司——抢占5G市场
- 中山农情统计分析系统项目实施与管理策略
- XX省中小学智慧校园建设实施方案
- 中山农情统计分析系统项目实施方案
- MATLAB函数详解:从Text到Size的实用指南
- 考虑速度与加速度限制的工业机器人轨迹规划与实时补偿算法
- Matlab进行统计回归分析:从单因素到双因素方差分析
- 智慧灯杆数据运营公司策划书:抢占5G市场,打造智慧城市新载体
- Photoshop基础与色彩知识:信息时代的PS认证考试全攻略
- Photoshop技能测试:核心概念与操作
- Photoshop试题与答案详解
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功