CycleGAN论文.pdf_循环生成对抗网络

cycleGAN

原文

需积分: 0 897 浏览量更新于2023-05-25 评论 1 收藏 7.65MB PDF 举报

身份认证购VIP最低享 7 折!

领优惠券(最高得80元）

资源详情

资源评论

资源推荐

Unpaired Image-to-Image Translation

using Cycle-Consistent Adversarial Networks

Jun-Yan Zhu

∗

Taesung Park

∗

Phillip Isola Alexei A. Efros

Berkeley AI Research (BAIR) laboratory, UC Berkeley

Zebras Horses

horse zebra

zebra horse

Summer Winter

summer winter

winter summer

Photograph Van Gogh CezanneMonet Ukiyo-e

Monet Photos

Monet photo

photo Monet

Figure 1: Given any two unordered image collections X and Y , our algorithm learns to automatically “translate” an image

from one into the other and vice versa: (left) Monet paintings and landscape photos from Flickr; (center) zebras and horses

from ImageNet; (right) summer and winter Yosemite photos from Flickr. Example application (bottom): using a collection

of paintings of famous artists, our method learns to render natural photographs into the respective styles.

Abstract

Image-to-image translation is a class of vision and

graphics problems where the goal is to learn the mapping

between an input image and an output image using a train-

ing set of aligned image pairs. However, for many tasks,

paired training data will not be available. We present an

approach for learning to translate an image from a source

domain X to a target domain Y in the absence of paired

examples. Our goal is to learn a mapping G : X → Y

such that the distribution of images from G(X) is indistin-

guishable from the distribution Y using an adversarial loss.

Because this mapping is highly under-constrained, we cou-

ple it with an inverse mapping F : Y → X and introduce a

cycle consistency loss to enforce F (G(X)) ≈ X (and vice

versa). Qualitative results are presented on several tasks

where paired training data does not exist, including collec-

tion style transfer, object transﬁguration, season transfer,

photo enhancement, etc. Quantitative comparisons against

several prior methods demonstrate the superiority of our

approach.

1. Introduction

What did Claude Monet see as he placed his easel by the

bank of the Seine near Argenteuil on a lovely spring day

in 1873 (Figure 1, top-left)? A color photograph, had it

been invented, may have documented a crisp blue sky and

a glassy river reﬂecting it. Monet conveyed his impression

of this same scene through wispy brush strokes and a bright

palette.

What if Monet had happened upon the little harbor in

Cassis on a cool summer evening (Figure 1, bottom-left)?

A brief stroll through a gallery of Monet paintings makes it

possible to imagine how he would have rendered the scene:

perhaps in pastel shades, with abrupt dabs of paint, and a

somewhat ﬂattened dynamic range.

We can imagine all this despite never having seen a side

by side example of a Monet painting next to a photo of the

scene he painted. Instead, we have knowledge of the set of

Monet paintings and of the set of landscape photographs.

We can reason about the stylistic differences between these

* indicates equal contribution

arXiv:1703.10593v6 [cs.CV] 15 Nov 2018

…

Paired Unpaired

Figure 2: Paired training data (left) consists of training ex-

amples {x

, y

}

i=1

, where the correspondence between x

and y

exists [22]. We instead consider unpaired training

data (right), consisting of a source set {x

}

i=1

∈ X)

and a target set {y

}

j=1

∈ Y ), with no information pro-

vided as to which x

matches which y

two sets, and thereby imagine what a scene might look like

if we were to “translate” it from one set into the other.

In this paper, we present a method that can learn to do the

same: capturing special characteristics of one image col-

lection and ﬁguring out how these characteristics could be

translated into the other image collection, all in the absence

of any paired training examples.

This problem can be more broadly described as image-

to-image translation [22], converting an image from one

representation of a given scene, x, to another, y, e.g.,

grayscale to color, image to semantic labels, edge-map to

photograph. Years of research in computer vision, image

processing, computational photography, and graphics have

produced powerful translation systems in the supervised

setting, where example image pairs {x

, y

}

i=1

are avail-

able (Figure 2, left), e.g., [11, 19, 22, 23, 28, 33, 45, 56, 58,

62]. However, obtaining paired training data can be difﬁcult

and expensive. For example, only a couple of datasets ex-

ist for tasks like semantic segmentation (e.g., [4]), and they

are relatively small. Obtaining input-output pairs for graph-

ics tasks like artistic stylization can be even more difﬁcult

since the desired output is highly complex, typically requir-

ing artistic authoring. For many tasks, like object transﬁgu-

ration (e.g., zebra↔horse, Figure 1 top-middle), the desired

output is not even well-deﬁned.

We therefore seek an algorithm that can learn to trans-

late between domains without paired input-output examples

(Figure 2, right). We assume there is some underlying rela-

tionship between the domains – for example, that they are

two different renderings of the same underlying scene – and

seek to learn that relationship. Although we lack supervi-

sion in the form of paired examples, we can exploit super-

vision at the level of sets: we are given one set of images in

domain X and a different set in domain Y . We may train

a mapping G : X → Y such that the output ˆy = G(x),

x ∈ X, is indistinguishable from images y ∈ Y by an ad-

versary trained to classify ˆy apart from y. In theory, this ob-

jective can induce an output distribution over ˆy that matches

the empirical distribution p

data

(y) (in general, this requires

G to be stochastic) [16]. The optimal G thereby translates

the domain X to a domain

Y distributed identically to Y .

However, such a translation does not guarantee that an in-

dividual input x and output y are paired up in a meaningful

way – there are inﬁnitely many mappings G that will in-

duce the same distribution over ˆy. Moreover, in practice,

we have found it difﬁcult to optimize the adversarial objec-

tive in isolation: standard procedures often lead to the well-

known problem of mode collapse, where all input images

map to the same output image and the optimization fails to

make progress [15].

These issues call for adding more structure to our ob-

jective. Therefore, we exploit the property that translation

should be “cycle consistent”, in the sense that if we trans-

late, e.g., a sentence from English to French, and then trans-

late it back from French to English, we should arrive back

at the original sentence [3]. Mathematically, if we have a

translator G : X → Y and another translator F : Y → X,

then G and F should be inverses of each other, and both

mappings should be bijections. We apply this structural as-

sumption by training both the mapping G and F simultane-

ously, and adding a cycle consistency loss [64] that encour-

ages F (G(x)) ≈ x and G(F (y)) ≈ y. Combining this loss

with adversarial losses on domains X and Y yields our full

objective for unpaired image-to-image translation.

We apply our method to a wide range of applications,

including collection style transfer, object transﬁguration,

season transfer and photo enhancement. We also compare

against previous approaches that rely either on hand-deﬁned

factorizations of style and content, or on shared embed-

ding functions, and show that our method outperforms these

baselines. We provide both PyTorch and Torch implemen-

tations. Check out more results at our website.

2. Related work

Generative Adversarial Networks (GANs) [16, 63]

have achieved impressive results in image generation [6,

39], image editing [66], and representation learning [39, 43,

37]. Recent methods adopt the same idea for conditional

image generation applications, such as text2image [41], im-

age inpainting [38], and future prediction [36], as well as to

other domains like videos [54] and 3D data [57]. The key to

GANs’ success is the idea of an adversarial loss that forces

the generated images to be, in principle, indistinguishable

from real photos. This loss is particularly powerful for im-

age generation tasks, as this is exactly the objective that

much of computer graphics aims to optimize. We adopt an

adversarial loss to learn the mapping such that the translated

(

(a)

(b)

(c)

cycle-consistency

loss

cycle-consistency

loss

ˆy

ˆx

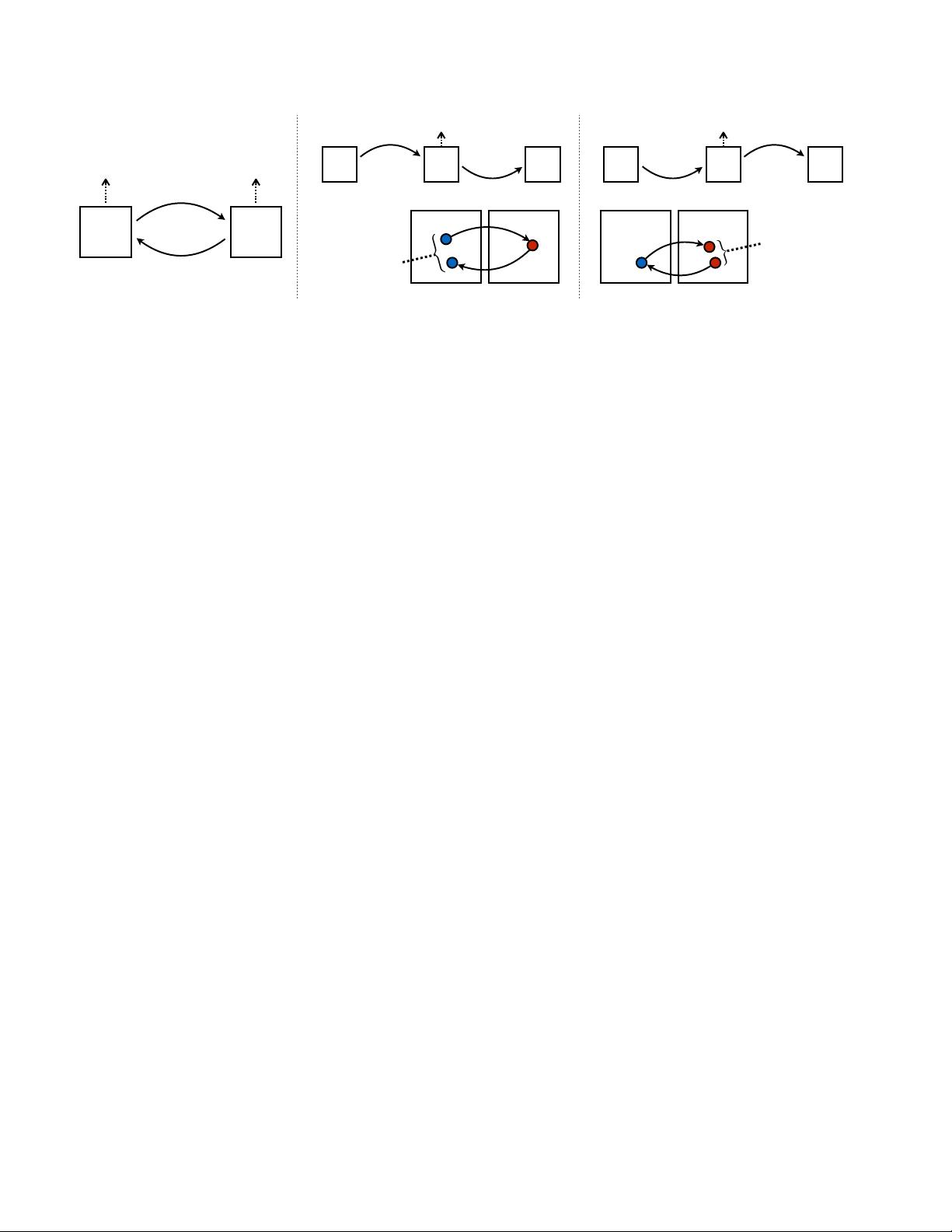
Figure 3: (a) Our model contains two mapping functions G : X → Y and F : Y → X, and associated adversarial

discriminators D

and D

. D

encourages G to translate X into outputs indistinguishable from domain Y , and vice versa

for D

and F. To further regularize the mappings, we introduce two cycle consistency losses that capture the intuition that if

we translate from one domain to the other and back again we should arrive at where we started: (b) forward cycle-consistency

loss: x → G(x) → F (G(x)) ≈ x, and (c) backward cycle-consistency loss: y → F (y) → G(F (y)) ≈ y

images cannot be distinguished from images in the target

domain.

Image-to-Image Translation The idea of image-to-

image translation goes back at least to Hertzmann et al.’s

Image Analogies [19], who employ a non-parametric tex-

ture model [10] on a single input-output training image pair.

More recent approaches use a dataset of input-output exam-

ples to learn a parametric translation function using CNNs

(e.g., [33]). Our approach builds on the “pix2pix” frame-

work of Isola et al. [22], which uses a conditional generative

adversarial network [16] to learn a mapping from input to

output images. Similar ideas have been applied to various

tasks such as generating photographs from sketches [44] or

from attribute and semantic layouts [25]. However, unlike

the above prior work, we learn the mapping without paired

training examples.

Unpaired Image-to-Image Translation Several other

methods also tackle the unpaired setting, where the goal is

to relate two data domains: X and Y . Rosales et al. [42]

propose a Bayesian framework that includes a prior based

on a patch-based Markov random ﬁeld computed from a

source image and a likelihood term obtained from multiple

style images. More recently, CoGAN [32] and cross-modal

scene networks [1] use a weight-sharing strategy to learn a

common representation across domains. Concurrent to our

method, Liu et al. [31] extends the above framework with

a combination of variational autoencoders [27] and genera-

tive adversarial networks [16]. Another line of concurrent

work [46, 49, 2] encourages the input and output to share

speciﬁc “content” features even though they may differ in

“style“. These methods also use adversarial networks, with

additional terms to enforce the output to be close to the input

in a predeﬁned metric space, such as class label space [2],

image pixel space [46], and image feature space [49].

Unlike the above approaches, our formulation does not

rely on any task-speciﬁc, predeﬁned similarity function be-

tween the input and output, nor do we assume that the input

and output have to lie in the same low-dimensional embed-

ding space. This makes our method a general-purpose solu-

tion for many vision and graphics tasks. We directly com-

pare against several prior and contemporary approaches in

Section 5.1.

Cycle Consistency The idea of using transitivity as a

way to regularize structured data has a long history. In

visual tracking, enforcing simple forward-backward con-

sistency has been a standard trick for decades [24, 48].

In the language domain, verifying and improving transla-

tions via “back translation and reconciliation” is a technique

used by human translators [3] (including, humorously, by

Mark Twain [51]), as well as by machines [17]. More

recently, higher-order cycle consistency has been used in

structure from motion [61], 3D shape matching [21], co-

segmentation [55], dense semantic alignment [65, 64], and

depth estimation [14]. Of these, Zhou et al. [64] and Go-

dard et al. [14] are most similar to our work, as they use a

cycle consistency loss as a way of using transitivity to su-

pervise CNN training. In this work, we are introducing a

similar loss to push G and F to be consistent with each

other. Concurrent with our work, in these same proceed-

ings, Yi et al. [59] independently use a similar objective

for unpaired image-to-image translation, inspired by dual

learning in machine translation [17].

Neural Style Transfer [13, 23, 52, 12] is another way

to perform image-to-image translation, which synthesizes a

novel image by combining the content of one image with

the style of another image (typically a painting) based on

matching the Gram matrix statistics of pre-trained deep fea-

tures. Our primary focus, on the other hand, is learning

the mapping between two image collections, rather than be-

tween two speciﬁc images, by trying to capture correspon-

dences between higher-level appearance structures. There-

fore, our method can be applied to other tasks, such as

painting→ photo, object transﬁguration, etc. where single

sample transfer methods do not perform well. We compare

these two methods in Section 5.2.

3. Formulation

Our goal is to learn mapping functions between two

domains X and Y given training samples {x

}

i=1

where

∈ X and {y

}

j=1

where y

∈ Y

. We denote the data

distribution as x ∼ p

data

(x) and y ∼ p

data

(y). As illus-

trated in Figure 3 (a), our model includes two mappings

G : X → Y and F : Y → X. In addition, we in-

troduce two adversarial discriminators D

and D

, where

aims to distinguish between images {x} and translated

images {F (y)}; in the same way, D

aims to discriminate

between {y} and {G(x)}. Our objective contains two types

of terms: adversarial losses [16] for matching the distribu-

tion of generated images to the data distribution in the target

domain; and cycle consistency losses to prevent the learned

mappings G and F from contradicting each other.

3.1. Adversarial Loss

We apply adversarial losses [16] to both mapping func-

tions. For the mapping function G : X → Y and its dis-

criminator D

, we express the objective as:

GAN

(G, D

, X, Y ) = E

y ∼p

data

(y )

[log D

(y)]

+ E

x∼p

data

(x)

[log(1 − D

(G(x))],

(1)

where G tries to generate images G(x) that look similar to

images from domain Y , while D

aims to distinguish be-

tween translated samples G(x) and real samples y. G aims

to minimize this objective against an adversary D that tries

to maximize it, i.e., min

max

GAN

(G, D

, X, Y ).

We introduce a similar adversarial loss for the mapping

function F : Y → X and its discriminator D

as well:

i.e., min

max

GAN

(F, D

, Y, X).

3.2. Cycle Consistency Loss

Adversarial training can, in theory, learn mappings G

and F that produce outputs identically distributed as target

domains Y and X respectively (strictly speaking, this re-

quires G and F to be stochastic functions) [15]. However,

with large enough capacity, a network can map the same

set of input images to any random permutation of images in

the target domain, where any of the learned mappings can

induce an output distribution that matches the target dis-

tribution. Thus, adversarial losses alone cannot guarantee

that the learned function can map an individual input x

a desired output y

. To further reduce the space of possi-

ble mapping functions, we argue that the learned mapping

We often omit the subscript i and j for simplicity.

Input 𝑥 Output 𝐺(𝑥) Reconstruction F(𝐺 𝑥 )

Figure 4: The input images x, output images G(x) and the

reconstructed images F (G(x)) from various experiments.

From top to bottom: photo↔Cezanne, horses↔zebras,

winter→summer Yosemite, aerial photos↔Google maps.

functions should be cycle-consistent: as shown in Figure 3

(b), for each image x from domain X, the image translation

cycle should be able to bring x back to the original image,

i.e., x → G(x) → F (G(x)) ≈ x. We call this forward cy-

cle consistency. Similarly, as illustrated in Figure 3 (c), for

each image y from domain Y , G and F should also satisfy

backward cycle consistency: y → F (y) → G(F (y)) ≈ y.

We incentivize this behavior using a cycle consistency loss:

cyc

(G, F ) = E

x∼p

data

(x)

[kF (G(x)) − xk

]

+ E

y∼p

data

(y )

[kG(F (y)) − yk

]. (2)

In preliminary experiments, we also tried replacing the L1

norm in this loss with an adversarial loss between F(G(x))

and x, and between G(F (y)) and y, but did not observe

improved performance.

The behavior induced by the cycle consistency loss can

be observed in Figure 4: the reconstructed images F(G(x))

end up matching closely to the input images x.

3.3. Full Objective

Our full objective is:

L(G, F, D

, D

) =L

GAN

(G, D

, X, Y )

+ L

GAN

(F, D

, Y, X)

+ λL

cyc

(G, F ), (3)

剩余17页未读，继续阅读

weixin_41999309

粉丝: 0
资源: 1

会员权益专享

CycleGAN论文.pdf

评论0

会员权益专享

最新资源

CycleGAN论文.pdf

评论0

给我推荐20个比较流行的AI作画模型

GAN-CycleGAN.pptx

给我推荐20个比较流行的AI作画模型源码

cyclegan stylegan

cyclegan tf2代码

CycleGAN的原理

给我推荐20个比较流行的计算机视觉模型

用pytorch写CycleGAN

cyclegan tensorflow2.0

pytorch-cyclegan-and-pix2pix

cyclegan和pix2pix区别

基于CycleGAN的艺术风格迁移

给我推荐20个比较流行的CNN模型

cyclegan 的实现

详细介绍一下CycleGAN、SRGAN、EDSR、ESRGAN

CycleGAN中欺骗相反域的鉴别器是什么意思

Skiena-The_Algorithm_Design_Manual.pdf

帮我写一个cycleGAN的代码

日语学习资料料理工具名称类

会员权益专享

最新资源