"多样树结构应用及关系解析:二叉数、搜索树、红黑树、AVL树、B树和B*树"
需积分: 9 69 浏览量
更新于2024-04-16
收藏 1.56MB DOCX 举报
树是计算机科学中常见的数据结构,其中包括二叉树、二叉搜索树、红黑树、AVL树、B树、B+树、B*树等等。这些树之间有着不同的特性和应用场景,下面将对它们进行简要总结。
首先是二叉树,它是一种每个节点最多有两个子节点的树结构。二叉搜索树(BST)是一种特殊的二叉树,其左子树的所有节点值均小于根节点的值,右子树的所有节点值均大于根节点的值。BST的特点是可以在O(logn)的时间复杂度内进行查找、插入和删除操作,但是如果树过于倾斜,可能会导致退化为链表,时间复杂度变为O(n)。
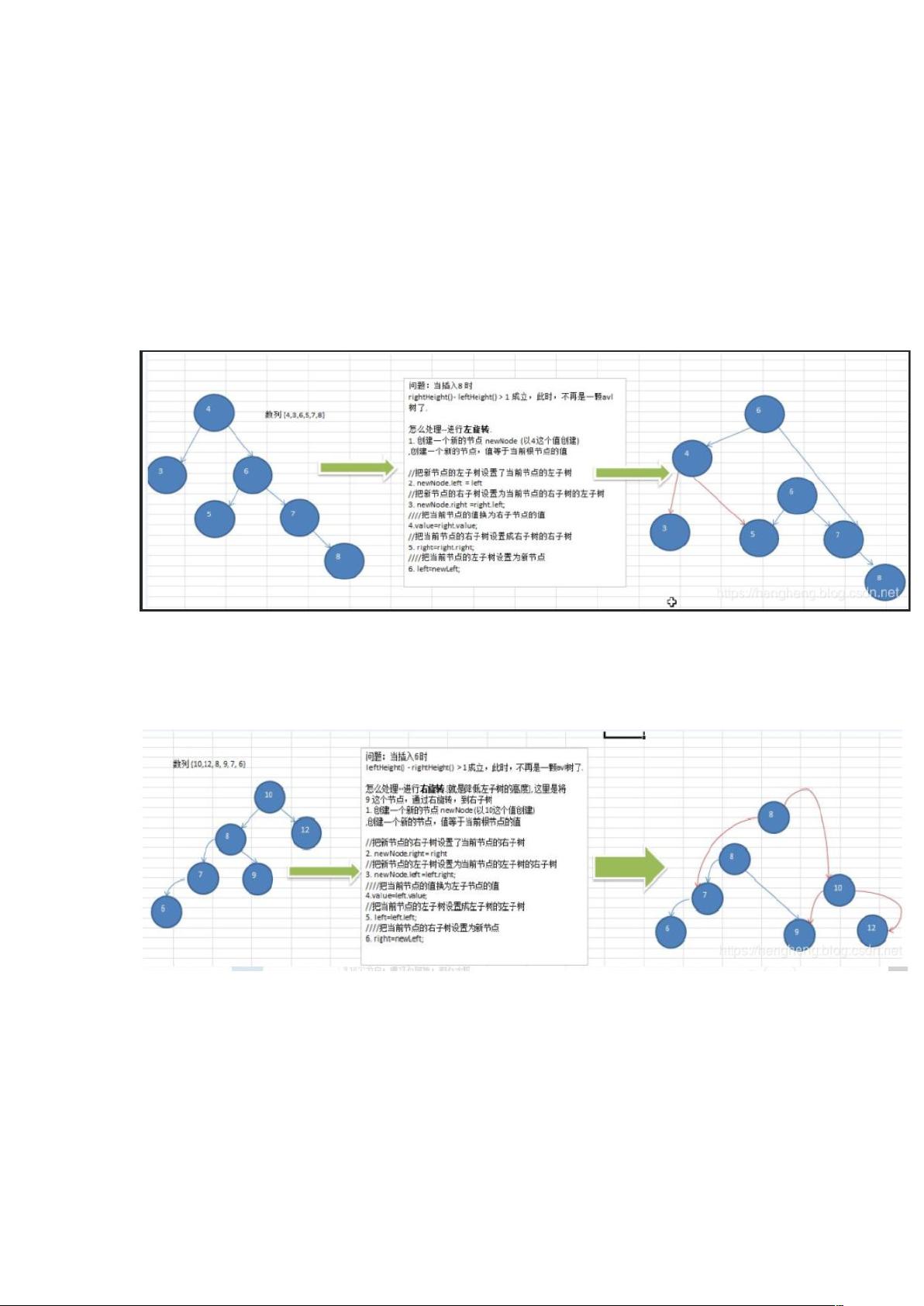
为了解决BST退化为链表的问题,产生了平衡二叉树,其中AVL树是最经典的一种。AVL树保持了树的平衡性,即任意节点的左右子树高度差不超过1,从而保证了查找、插入、删除等操作的时间复杂度为O(logn)。但是AVL树的局限性在于对平衡的要求过高,导致在插入和删除时可能需要频繁地进行旋转操作,影响性能。
为了解决AVL树频繁旋转的问题,出现了红黑树,它是一种近似平衡的二叉搜索树。红黑树在保持了较好的平衡性的同时,尽可能地减少了旋转的次数,优化了性能。红黑树是一种自平衡二叉搜索树,它保证了从根到叶子的最长路径不会超过最短路径的两倍,因此时间复杂度也是O(logn)。
另外,还有一种多路搜索树—B树,它是一种自平衡的树状数据结构,通常用于数据库和文件系统中。B树允许每个节点有多个子节点,从而减少了树的高度,提高了查找效率。B树的变种B+树和B*树在B树的基础上进行了优化,增加了指向叶子节点的指针,进一步提高了IO操作性能。
在实际应用中,各种树结构都有自己的适用场景。BST适合于静态数据集合,但不适用于动态更新频繁的情况;AVL树适用于对插入和删除操作次数远远超过查询操作的情况;红黑树适用于动态插入和删除操作频繁的情况,且对性能要求较高时;B树适用于大规模存储数据的场景,如数据库索引;哈夫曼树则适用于对频繁出现的字符进行编码和解码操作。
总的来说,树是计算机科学中非常重要的数据结构,各种树结构都有自己的特点和应用场景,可以根据具体需求选择合适的树进行应用。同时,在实际应用中也可以根据需求进行树的组合和优化,以提高系统性能和效率。
2021-01-07 上传
2023-03-13 上传
2021-12-29 上传
2022-11-11 上传
2022-07-06 上传
2022-07-14 上传
2022-07-14 上传
lo_nanase_ve
- 粉丝: 1
- 资源: 1
最新资源
- 探索数据转换实验平台在设备装置中的应用
- 使用git-log-to-tikz.py将Git日志转换为TIKZ图形
- 小栗子源码2.9.3版本发布
- 使用Tinder-Hack-Client实现Tinder API交互
- Android Studio新模板:个性化Material Design导航抽屉
- React API分页模块:数据获取与页面管理
- C语言实现顺序表的动态分配方法
- 光催化分解水产氢固溶体催化剂制备技术揭秘
- VS2013环境下tinyxml库的32位与64位编译指南
- 网易云歌词情感分析系统实现与架构
- React应用展示GitHub用户详细信息及项目分析
- LayUI2.1.6帮助文档API功能详解
- 全栈开发实现的chatgpt应用可打包小程序/H5/App
- C++实现顺序表的动态内存分配技术
- Java制作水果格斗游戏:策略与随机性的结合
- 基于若依框架的后台管理系统开发实例解析