KMP算法深度解析：提升字符串匹配效率

"KMP字符串模式匹配是一种高效的算法，用于在一个字符串中查找另一个字符串的出现位置，其时间复杂度为O(m+n)，优于简单的暴力匹配算法。KMP算法避免了不必要的回溯，通过预处理得到部分匹配表，使得在发生不匹配时可以直接跳过已匹配的部分，提高效率。本文将详细解释KMP算法的工作原理和实现过程，并通过实例展示其运行机制。" KMP算法是由Knuth、Morris和Pratt三位学者提出的，它的核心思想在于利用模式串（要查找的子串）的已匹配部分信息，避免在失配时完全回溯。简单匹配算法在遇到不匹配时会将主串下标回溯到0，而KMP算法则根据一个叫做“最长公共前后缀”的概念，计算出一个部分匹配表，指导匹配过程。 一、简单匹配算法 简单匹配算法，也称为暴力匹配，其基本思路是从主串S的每个位置开始，依次与模式串T进行逐字符比较。如果所有字符都匹配成功，就找到了模式串在主串中的位置。否则，如果遇到不匹配，就需要将主串下标i回溯到失配字符的下一个位置，模式串下标j回溯到0，再重新开始比较。这种做法在模式串较长时效率低下，因为它可能会重复比较已匹配的字符。 二、KMP匹配算法 KMP算法通过构造一个部分匹配表（也叫失配表），记录了模式串中每个位置的最长公共前后缀长度。在比较过程中，如果发生失配，可以根据部分匹配表直接跳过已匹配的字符，而不是回溯到模式串的起始位置。这样可以减少不必要的比较次数，提高效率。 1. 构造部分匹配表 对于模式串T，我们从左到右计算每个字符的最长公共前后缀。如果当前字符与前一个字符相同，那么最长公共前后缀就是前一个字符的最长公共前后缀加1；否则，最长公共前后缀为0。这个过程可以递归地计算出来，最终得到一个长度与模式串相等的数组。 2. KMP匹配过程 在主串S和模式串T的比较过程中，使用部分匹配表指导下一步的比较。如果当前字符匹配成功，就继续比较下一个字符；如果匹配失败，就根据部分匹配表的值，将模式串下标j移动到对应的值，主串下标i保持不变，继续比较。这个过程一直持续到找到匹配的子串或者主串遍历完。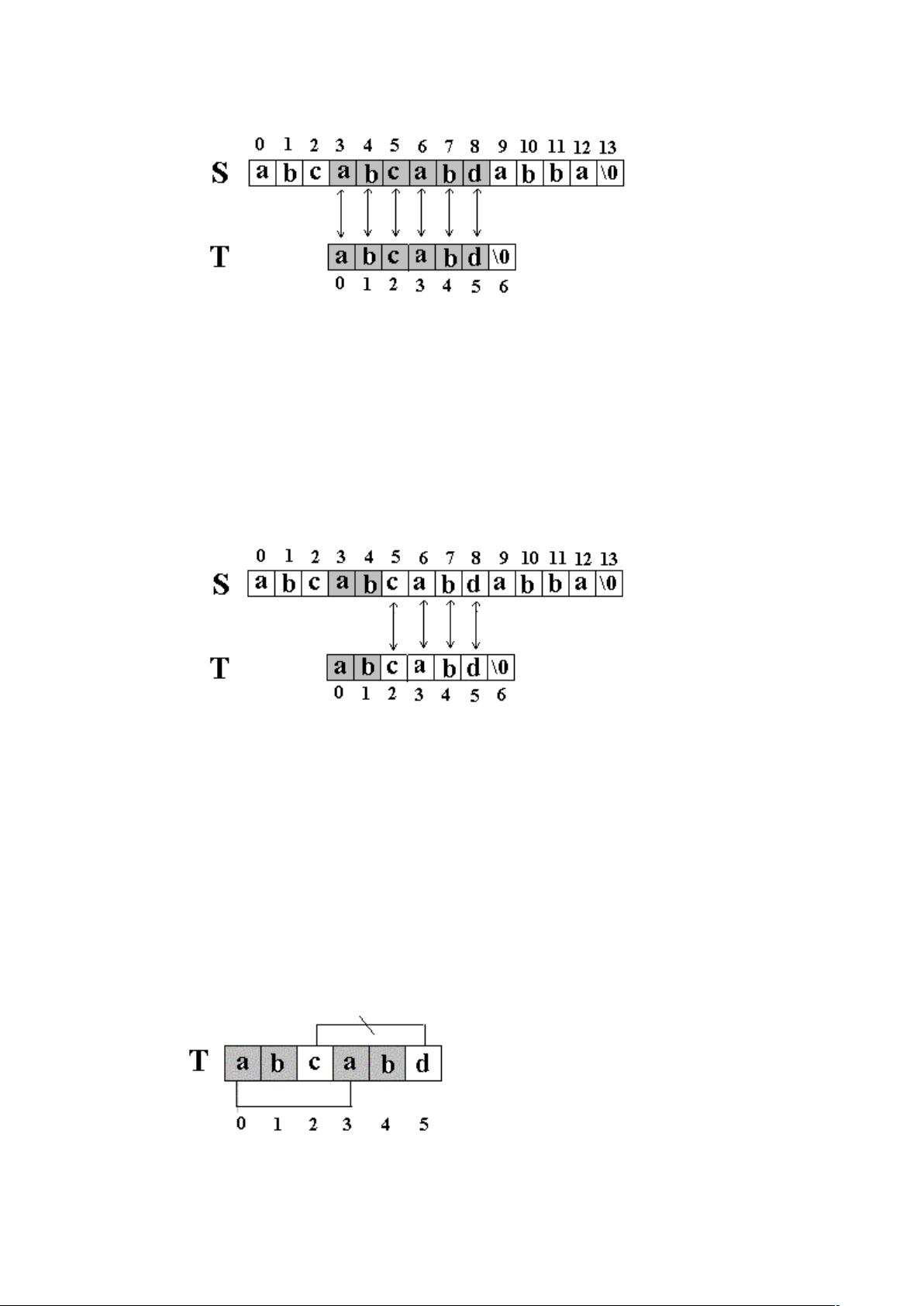 三、实例分析 以例子S="abcabcabdabba"和T="abcabd"为例，使用KMP算法进行匹配。首先构建部分匹配表，得到T的最长公共前后缀长度为[0, 0, 0, 1, 2, 1]。然后开始匹配： - 初始状态：i=0, j=0，比较S[0]=a和T[0]=a，匹配成功。 - i=1, j=1，比较S[1]=b和T[1]=b，匹配成功。 - i=2, j=2，比较S[2]=c和T[2]=c，匹配成功。 - i=3, j=3，比较S[3]=a和T[3]=a，匹配成功。 - i=4, j=4，比较S[4]=b和T[4]=b，匹配成功。 - i=5, j=5，比较S[5]=d和T[5]=d，失配。 此时，根据部分匹配表，j=1+1=2，模式串跳过已匹配的前两个字符，即T[2]=c，继续比较S[5]=d和T[2]=c，失配。j回到1，跳过已匹配的a，比较S[5]=d和T[1]=b，再次失配。j回到0，跳过整个已匹配部分，继续比较S[6]=a和T[0]=a，匹配成功。 以此类推，最终在S的下标为3的位置找到匹配的子串，返回结果为3。 总结，KMP算法通过优化匹配过程，减少了不必要的回溯，提高了字符串模式匹配的效率，尤其在模式串较长的情况下，性能优势更为明显。在实际编程中，KMP算法常用于文本处理、搜索算法等领域。