"数据结构实例教程（C语言版）：树和二叉树详解及应用技巧"

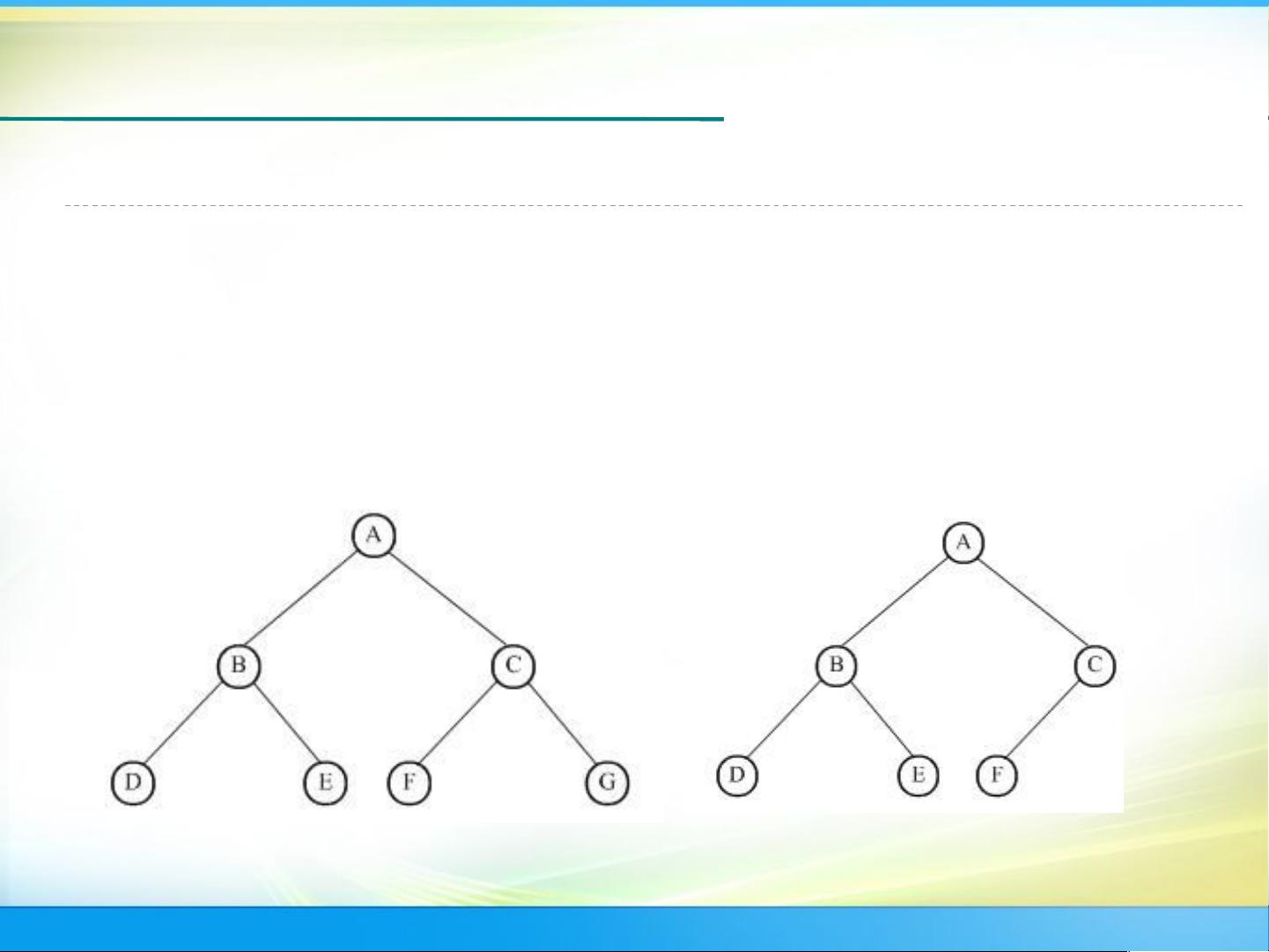
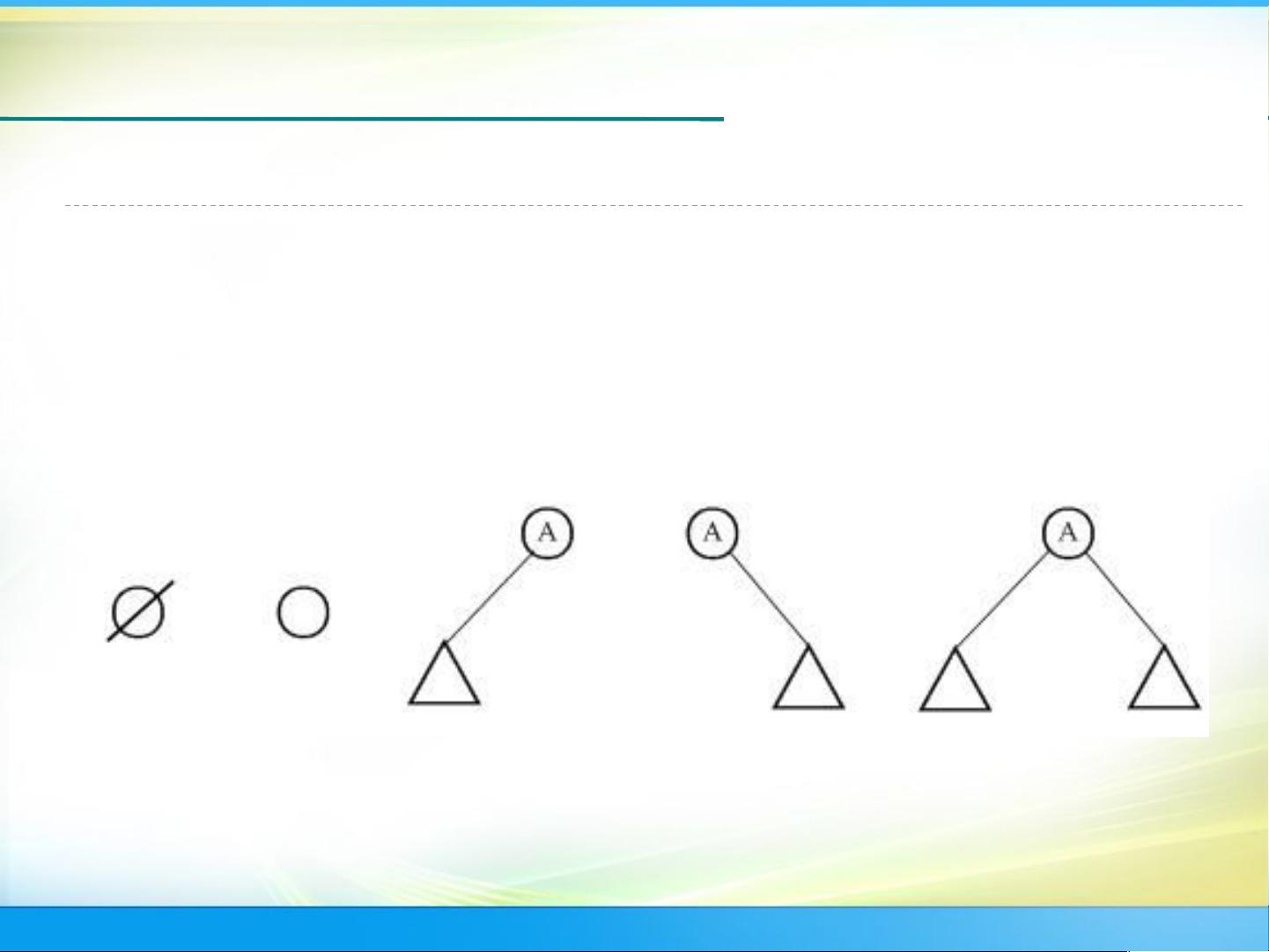
本章是数据结构实例教程（C语言版）中的第6章，主要讲解了树和二叉树的结构分析与应用。学习目标包括了解树的定义及基本术语、熟练掌握二叉树的性质、存储结构及遍历算法、掌握二叉树线索化的过程、了解哈夫曼树的构造方法及编码、掌握树的存储结构特点以及树和森林与二叉树之间的转换方法。 树形结构是一类重要的非线性结构，具有层次关系的结构，结点之间有分支。树是一个具有n(n≥0)个结点的有限集，其中结点之间存在特定的关系。树的基本术语包括结点的度和叶子（终端结点）。结点的度指结点拥有的孩子数目，而叶子是指度为零的结点。例如，在一个包含结点A、B、C、D、E、F、I、J、G和H的树中，结点A的度为3，而叶子结点包括C、E和I。 除了树的基本概念和术语之外，本章还详细介绍了二叉树的性质、存储结构和各种遍历算法。二叉树是一种特殊的树形结构，每个结点最多有两个子树，分别称为左子树和右子树。二叉树的遍历算法包括前序遍历、中序遍历和后序遍历，分别对应于先访问根结点、先访问左子树和先访问右子树的顺序。掌握了这些遍历算法，能够帮助程序员更好地理解和操作二叉树。 此外，本章还介绍了二叉树的线索化过程。线索化是一种优化二叉树遍历的方法，通过修改二叉树的空指针，将原本用于指向空子树的指针修改为指向中序遍历下的前驱或后继结点的指针，从而实现在不使用递归或栈的情况下遍历二叉树。 另外，本章还介绍了哈夫曼树的构造方法及编码。哈夫曼树是一种带权路径长度最短的树，通常用于数据压缩。通过构造哈夫曼树，可以得到最优的编码方式，从而实现数据的高效压缩和解压缩。 最后，本章还介绍了树的各种存储结构及特点，以及树和森林与二叉树之间的转换方法。掌握了这些知识，能够帮助程序员更好地选择合适的数据结构，并在实际应用中灵活运用。 通过学习本章内容，读者可以全面了解树和二叉树的结构，掌握它们的基本概念、存储结构、遍历算法以及相关的扩展知识，为在实际编程中应用树和二叉树提供了坚实的基础。同时，本章还对树和二叉树在实际应用中的一些特殊情况进行了讨论和应用，帮助读者更好地理解和应用树和二叉树在实际编程中的场景。