MATLAB频域转换实战：傅立叶与离散余弦变换

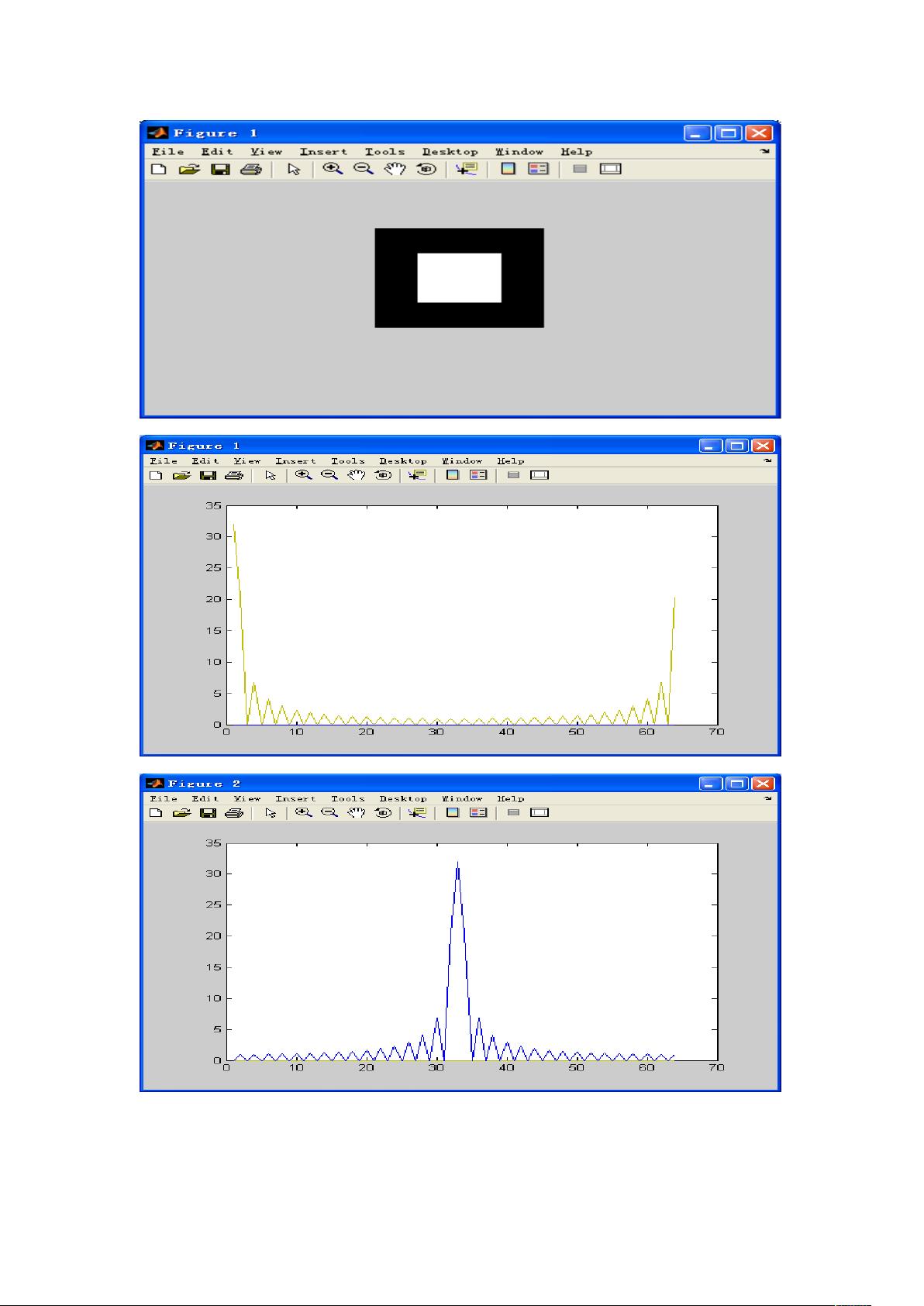
"MATLAB空间转换涉及频域空间转换，包括离散傅立叶变换(FFT)和离散余弦变换(DCT)。" 在MATLAB中，空间转换是信号处理和图像处理领域的重要工具，主要涉及到频域分析。离散傅立叶变换(Discrete Fourier Transform, DFT)和离散余弦变换(Discrete Cosine Transform, DCT)是两种常用的空间到频域的转换方法。 一、离散傅立叶变换(FFT) 离散傅立叶变换是一种将时域信号转换为频域表示的方法。MATLAB提供了fft函数来实现一维、二维乃至多维的DFT。例如，`fft(X)`用于计算一维DFT，`fft2(X)`用于二维DFT，而`fftn(X)`则适用于任意维度的DFT。`ifft`、`ifft2`和`ifftn`则是对应的逆变换函数，用于从频域返回到时域。在使用fft函数时，可以通过指定参数`N`来进行零填充或截取，以改变输出的长度。`fftshift`函数则用于重新排列DFT的结果，将频谱的零频率点移动到中心位置，便于可视化。 二、离散余弦变换(DCT) DCT是一种能量集中且具有正交性的变换，常用于图像压缩和信号去噪。MATLAB中的`dct2`函数用于二维DCT变换，`idct2`则为对应的逆变换。`dctmtx`函数用于生成DCT变换矩阵，这个矩阵在执行DCT时起到关键作用。通过指定参数`m`和`n`，可以在变换前后对输入矩阵进行零填充或剪裁，调整输出矩阵的大小。 三、实验内容与结果分析 在MATLAB中进行空间转换实验，通常会包含以下几个步骤： 1. 应用`fftshift`函数观察频谱的中心化效果，这对于理解和分析频谱分布至关重要。 2. 对不同类型的信号或图像应用DFT和DCT，比较它们在频域的特性。 3. 使用`ifftshift`将频域结果转换回原始位置，然后通过`ifft`或`idct`进行逆变换，验证变换的可逆性。 4. 分析变换前后的能量分布，了解信号或图像在时域和频域的特点。 5. 可能会涉及到零填充、截取等操作，研究它们如何影响频域解析度和计算效率。 通过这样的实验，可以深入理解频域空间转换的理论，并熟练掌握MATLAB中相关的函数操作。同时，实验结果的分析有助于实际问题的解决，如图像处理、信号分析等应用场景。