chirp Z 变换算法：高效计算与应用详解

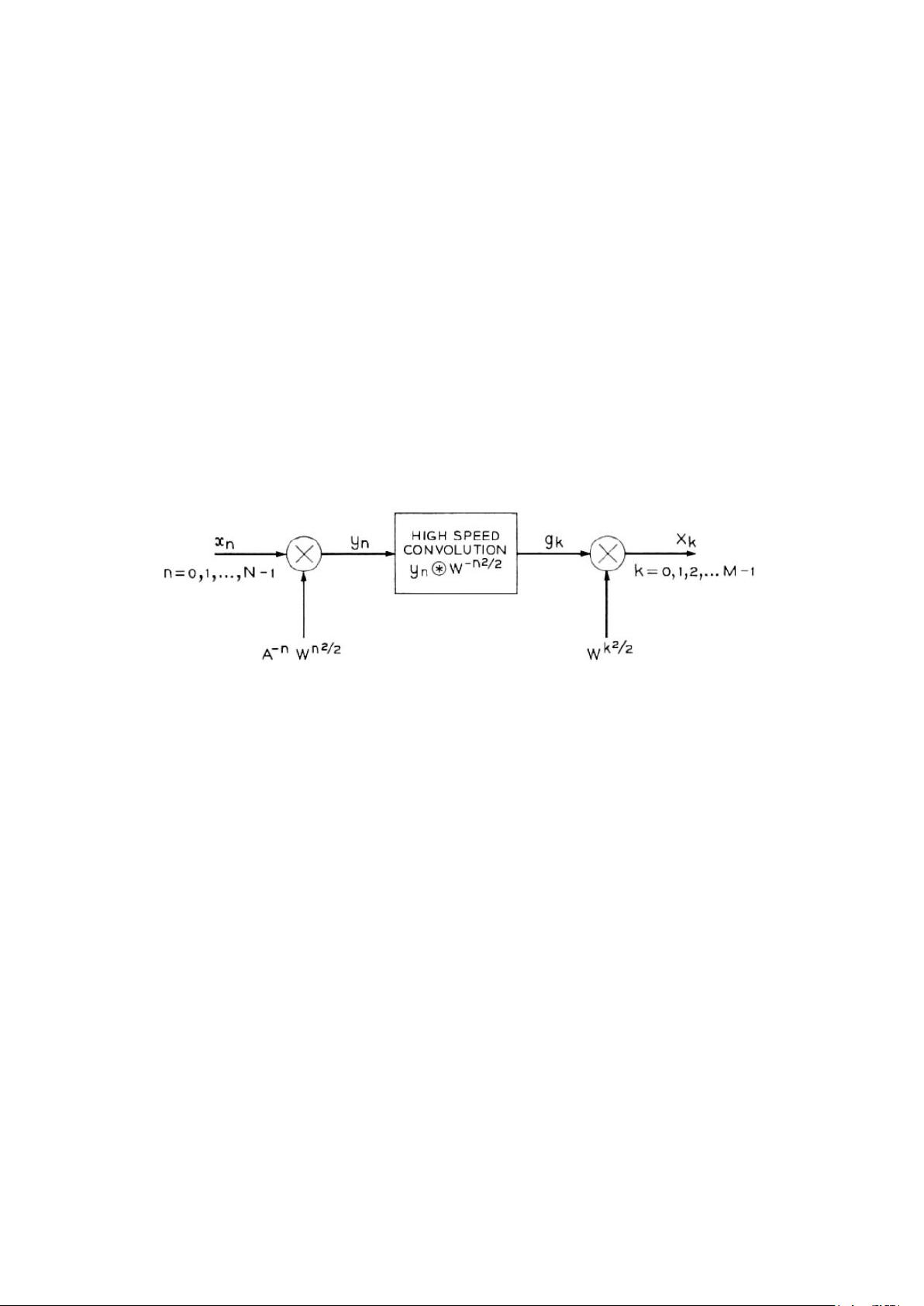
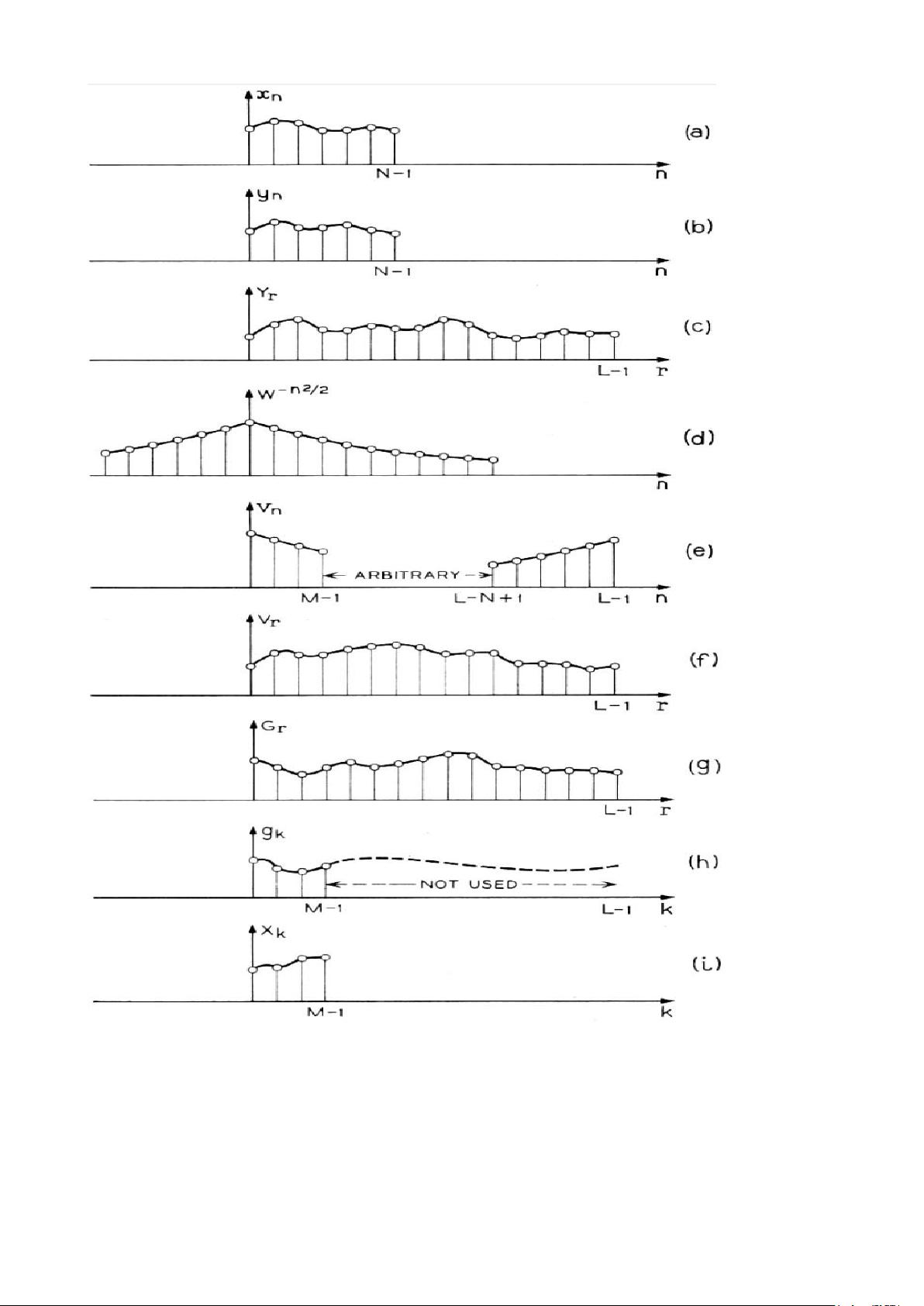
本文档深入探讨了Chirp Z变换算法及其在数字信号处理（DSP）领域的应用。Chirp Z变换是一种计算技术，用于数值评估一个包含N个样本序列的Z变换。这一算法的独特之处在于它能够在Z平面上的任意起点处，高效地计算出M个点上的Z变换，这些点沿着圆或螺旋路径分布，其角度间隔是任意常数。M和N可以是任意整数，这意味着相比于直接对每个点逐个进行Z变换，这种方法在M和N较大时具有显著的优势，计算时间复杂度大约为(M+N)log2(N+M)，相较于线性增长的时间节省明显。 算法的核心原理基于这样一个事实：Z变换在圆或螺旋路径上的值可以通过离散卷积来表示。因此，利用已知的高速卷积技术，如快速傅里叶变换（FFT），能够有效地执行Chirp Z变换。这使得算法在处理大规模数据时表现出高效性，特别适用于那些需要对信号频率特性进行分析、增强极点分辨率或者需要高分辨率频谱分析的应用场景。 具体的应用包括但不限于： 1. **极点增强**：在信号处理中，Chirp Z变换能帮助识别和增强频谱中的特定频率成分，这对于滤波器设计和系统稳定性分析至关重要。 2. **高分辨率频谱分析**：通过Chirp Z变换，可以实现更精细的频谱分析，从而在信号处理中获得更准确的信息，尤其是在噪声环境或复杂信号背景下。 3. **信号压缩与重构**：在通信和信号编码领域，Chirp Z变换可用于高效的数据压缩和恢复，减少存储需求并提高传输效率。 4. **滤波器设计**：该算法对于设计线性相位滤波器以及多带通滤波器有着潜在的优势，因为它们可以在Z平面上灵活控制滤波器的零点和极点位置。 5. **实时信号处理**：由于计算效率高，Chirp Z变换算法在实时信号处理系统中具有广泛应用潜力，如雷达、通信和音频处理等领域。 总结来说，Chirp Z变换算法是一个强大的工具，它通过利用离散卷积的性质和高效的计算方法，极大地提升了数字信号处理中的性能，特别是在处理大规模数据和需要高精度分析的任务中。