科学计算中的Matlab应用：代数方程与最优化问题求解【适合新手】

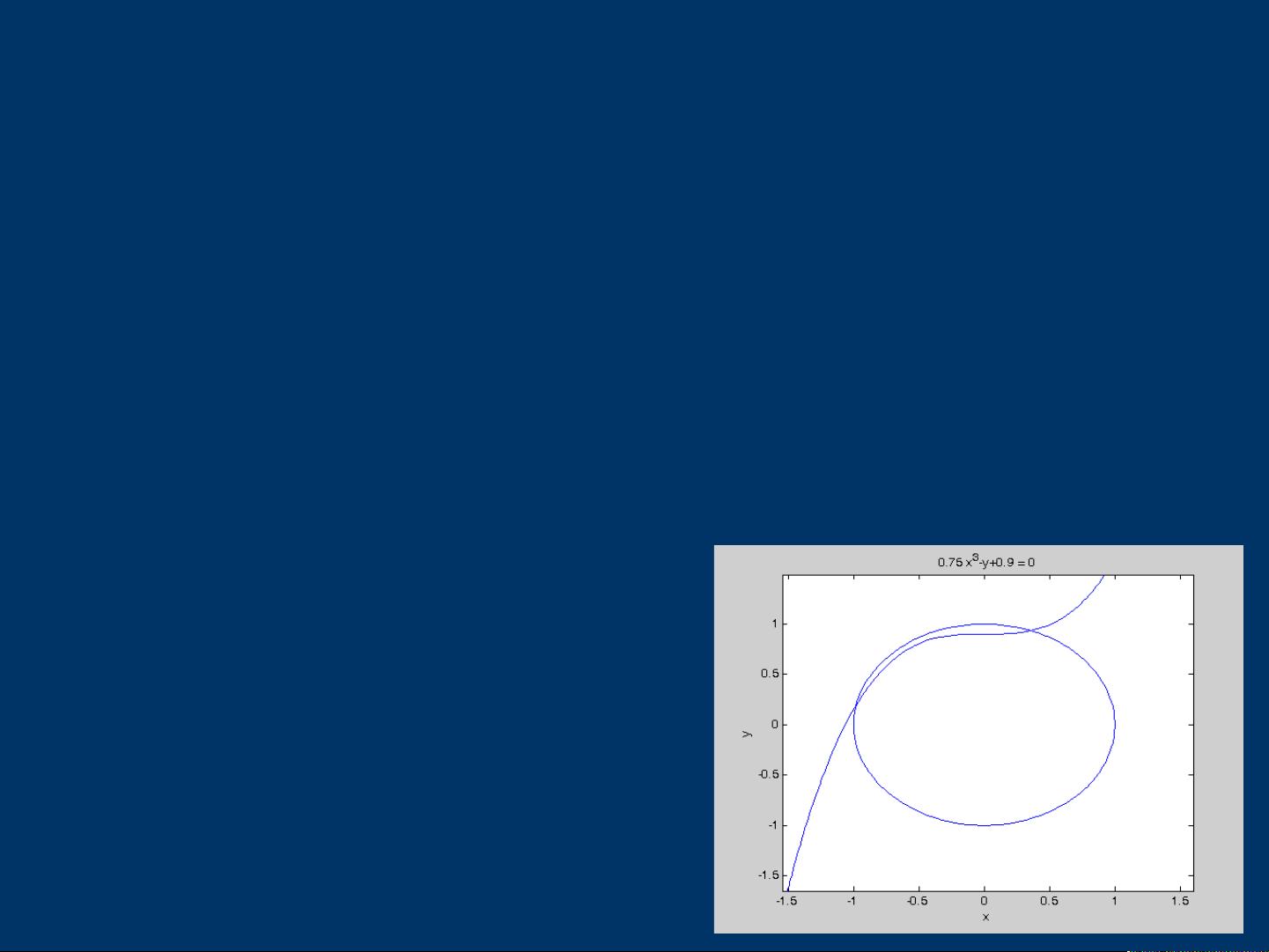
在科学计算中，MATLAB被广泛运用于代数方程与最优化问题的求解。第七章涵盖了代数方程、无约束最优化问题和有约束最优化问题的计算机求解，以及整数规划问题的求解。对于新手而言，本章节提供了适合入门的内容，包括代数方程的求解方法以及最优化问题的计算机求解技巧。 在代数方程的求解方面，本章介绍了图解法。通过MATLAB的ezplot函数，可以直观地展示一元和二元方程的图像，从而寻找方程的根。例如，针对一元方程exp(-3*t)*sin(4*t^2) - 4*exp(-0.5*t)*cos(2*t) - 0.5，可以使用ezplot函数绘制曲线，并通过syms函数计算特定点处的函数值，从而验证方程的解。对于二元方程，同样可以使用ezplot函数绘制两个方程的曲线，通过观察交点来求解方程。 需要注意的是，方程的图解法适用于一元和二元方程的求根问题，对于更高维度的方程，可能需要其他的求解方法。在无约束最优化问题的求解中，MATLAB提供了多种优化算法，可以帮助用户寻找函数的极小值或极大值。通过调用MATLAB的优化函数，用户可以指定目标函数和初始点，进行快速而准确的优化计算。对于有约束最优化问题，MATLAB同样提供了相应的优化函数，用户可以设置约束条件，求解满足约束的最优解。 此外，MATLAB还支持整数规划问题的计算机求解。整数规划问题是一类特殊的最优化问题，其中变量的取值限制为整数。在MATLAB中，可以使用专门的整数规划函数，如intlinprog，来求解这类问题，帮助用户在实际应用中找到最优的整数解。 总的来说，MATLAB在科学计算中的应用涵盖了代数方程与最优化问题的求解，为用户提供了丰富的工具和函数，帮助他们解决复杂的数学和优化问题。对于新手而言，通过学习本章节的内容，可以逐步掌握MATLAB在代数方程与最优化问题中的应用技巧，为未来的科学计算工作打下坚实的基础。