东北大学历年高数上期末试题集锦

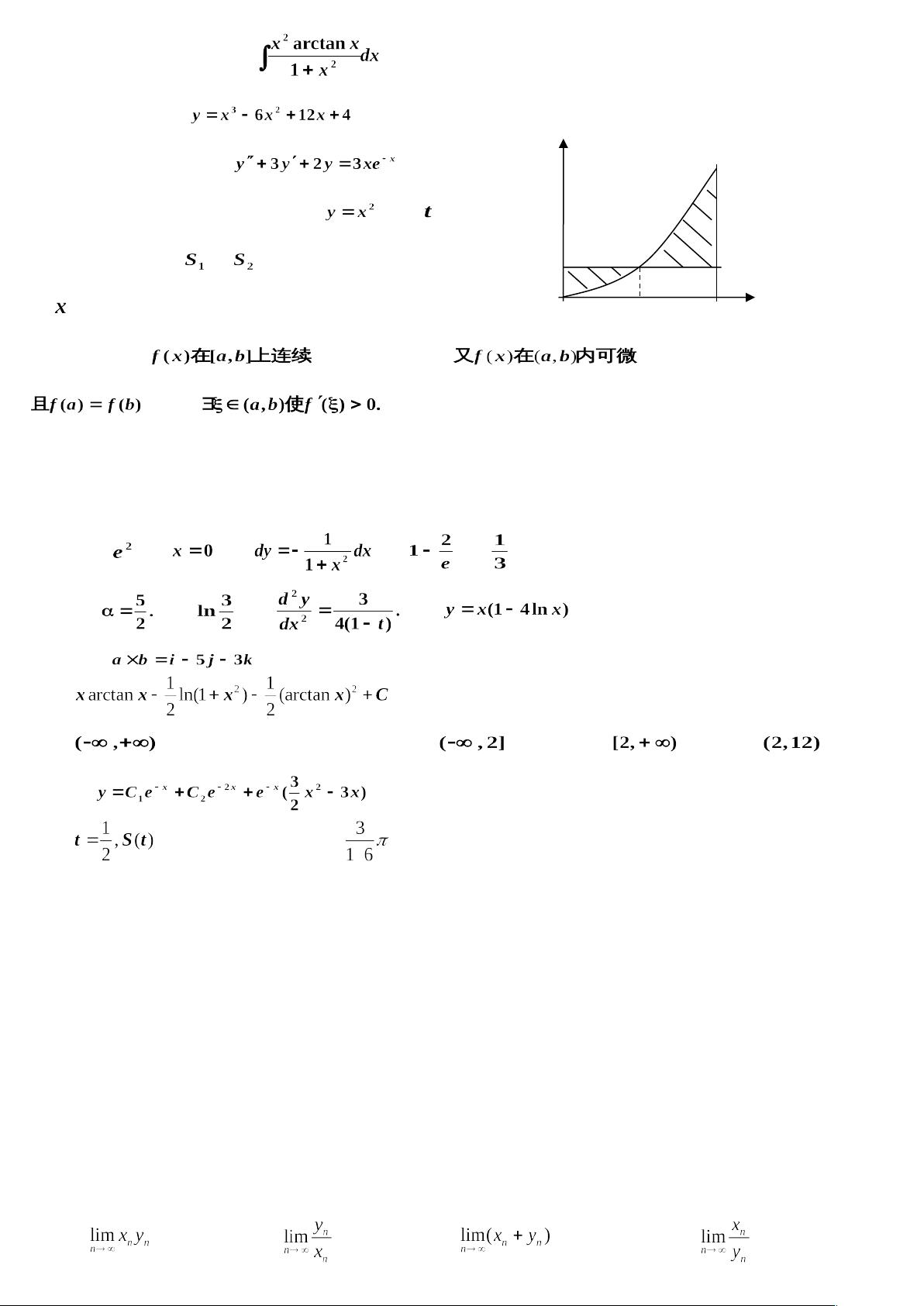
"东北大学高数上2005年至2014年的十年期末试题集，涵盖了填空题、选择题、计算题和解答题等类型，旨在测试学生的高等数学知识掌握情况，包括极限、微积分、方程求解、几何应用等方面。" 这篇资料主要涉及高等数学的相关知识点，具体包括以下几个方面： 1. **极限理论**：题目中出现的数列收敛性问题涉及到极限理论。例如，判断数列是否收敛、发散，以及极限的存在性。这需要理解并应用极限的基本性质和判定准则。 2. **可导性和微分**：部分题目考察函数在特定点的可导性，如第2题，要求找到使函数在某点可导的参数值。这涉及到可导性的定义，即函数在该点的左导数和右导数都存在且相等。 3. **微积分的应用**：如第4题讨论曲线的曲率最大值，这需要利用曲率公式，涉及微分学中的曲率概念。曲率是衡量曲线弯曲程度的量，与导数和二阶导数有关。 4. **方程的根**：第3题问及方程的正根数量，这需要分析方程的解的情况，可能需要用到二次方程的判别式或者更高阶方程的根的性质。 5. **多元函数微积分**：第5题提及的三阶连续导数与极值点和拐点的关系，涉及到多元函数的泰勒展开和极值理论。若三阶导数非零，那么该点可能是拐点，但不一定是极值点。 6. **线性代数与几何**：选择题中的第6题考察了直线与平面的位置关系，这需要理解线性方程组解的几何意义，以及线、面平行、垂直和相交的判定。 7. **微分方程**：计算题中可能包含微分方程的特解形式，如第6题，需要根据微分方程的特征来确定特解的形式。 8. **几何问题**：解答题中通常会有实际问题的应用，比如第1题的圆柱体体积最大值问题，需要用到优化方法，如拉格朗日乘数法；第2题的椭圆面积和旋转体体积计算，涉及积分的应用；第3题则可能涉及到平面束内的线性组合问题。 这些题目综合考察了高等数学的基础概念、理论和应用，对于理解和掌握高等数学知识体系至关重要。学生通过解决这些试题，可以提升对极限、微积分、方程解法、几何分析和应用问题的处理能力。