图像处理:深入理解离散傅里叶变换与频率域滤波
版权申诉
90 浏览量
更新于2024-07-01
收藏 3.33MB PPTX 举报
"Ch4 频率域滤波-1.pptx 是关于数字图像处理的资料,主要讲解了离散傅里叶变换(DFT)及其在图像增强中的应用,包括一维和二维DFT的概念,以及频率域滤波的重要性。"
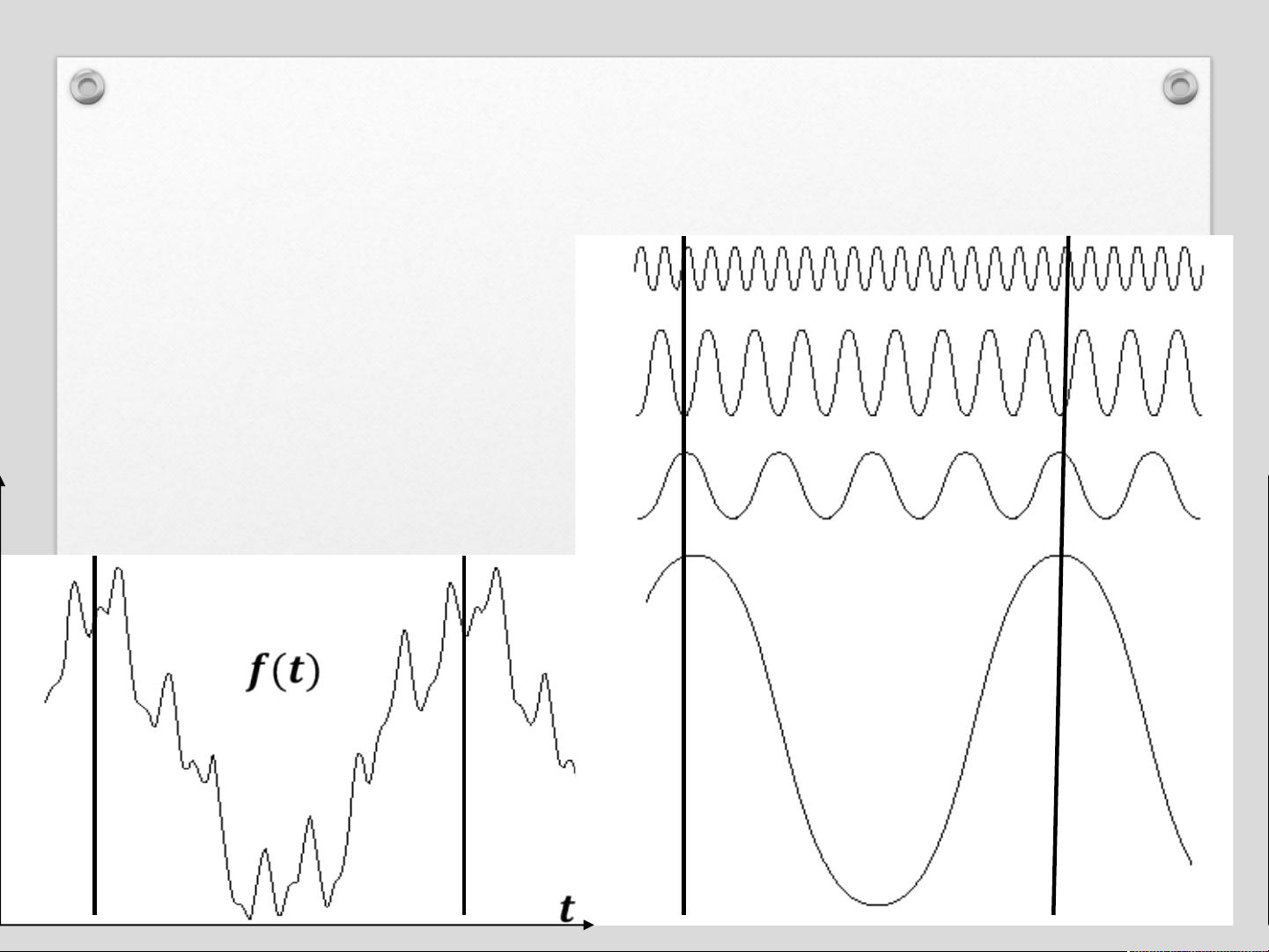
在数字图像处理领域,频率域滤波是一种重要的技术,它涉及到离散傅里叶变换。离散傅里叶变换(DFT)是将图像从空间域转换到频率域的关键工具,这一转换对于理解和处理图像的频率特性至关重要。DFT能够揭示图像中的高频和低频成分,这些成分与图像的细节和平滑区域相对应。
4.1 基本概念部分强调了在频率域研究图像增强的原因。因为图像的频率成分与图像的视觉特征有直接关系,比如高频成分对应图像的边缘和细节,而低频成分则代表图像的整体亮度和色调。通过在频率域进行操作,可以更直观地对这些特性进行增强或抑制,从而达到改善图像质量的目的。例如,通过滤波器设计,可以选择性地保留或消除某些频率成分,实现降噪、锐化等效果。
4.2 一维DFT是DFT的基础,它用于分析一维信号的频率成分。尽管图像通常是二维的,但一维DFT的概念对于理解二维DFT是很有帮助的。一维DFT将一个有限长度的序列转换为一组复数系数,这些系数表示信号的频率成分。
4.3 二维DFT是处理图像的主要手段,因为它考虑了图像在两个维度上的信息。二维DFT将图像矩阵转换为频谱矩阵,每个元素代表图像中某个特定频率的强度。这种转换使得我们可以直观地看到图像的高频和低频特征,并据此进行滤波操作。
傅里叶变换是基于傅里叶级数理论的,该理论表明任何周期性信号都可以表示为不同频率正弦波的线性组合。傅里叶的两大贡献是将周期信号用正弦函数的加权和表示,以及将非周期信号用正弦函数的加权积分表示。在图像处理中,虽然图像通常是非周期的,但可以通过傅里叶变换将其转换到频域,这样就可以利用傅里叶级数的概念来分析其频率成分。
通过欧拉公式,傅里叶级数可以进一步简化,以复数的形式表示,这使得计算更加便捷。在处理非周期信号时,使用离散傅里叶变换(DFT),它是在离散数据集上应用的傅里叶变换,特别适合于计算机处理。
总结来说,Ch4 频率域滤波的讲解深入探讨了DFT的基本概念、一维和二维DFT的计算以及它们在图像增强中的应用。通过频率域滤波,我们可以更有效地处理图像,改善其视觉效果,这对于图像处理和计算机视觉领域的各种应用至关重要。
2022-07-09 上传
123 浏览量
123 浏览量
104 浏览量
2021-02-21 上传