自动控制原理第二章：控制系统数学模型解析

"自动控制原理课件第二章，包含了控制系统数学模型的讲解，重点介绍了时域模型—微分方程和复域模型—传递函数，以及如何建立系统数学模型的方法，如解析法和实验法。内容包括控制系统的时域数学模型的建立步骤，并通过弹簧—质量—阻尼器系统和R-L-C电路的建模举例进行详细解释。" 在自动控制原理中，数学模型是描述控制系统中各个变量之间关系的数学表达式，对于理解和分析控制系统的动态行为至关重要。模型分为时域模型和复域模型。时域模型主要用微分方程来表示，它反映了系统动态变化的过程；而复域模型则通常采用传递函数，这在频率域分析中非常有用。 第二章主要探讨的是控制系统的时域数学模型，其建立通常遵循六个步骤：首先，明确输入和输出变量；其次，依据物理定律（如牛顿第二定律）列出原始方程；接着，处理中间变量，找出它们与输入和输出的关系；第四步，如果模型是非线性的，需要进行线性化处理；第五，标准化方程，使输入项和输出项分别位于方程的左右两边；最后，按照降幂顺序排列。 以弹簧—质量—阻尼器系统为例，输入是外力f(t)，输出是位移y(t)。通过牛顿第二定律可以列出原始方程，然后逐步消去中间变量（如加速度和速度），最终得到线性定常二阶微分方程式，该方程描述了系统动态响应与输入之间的关系。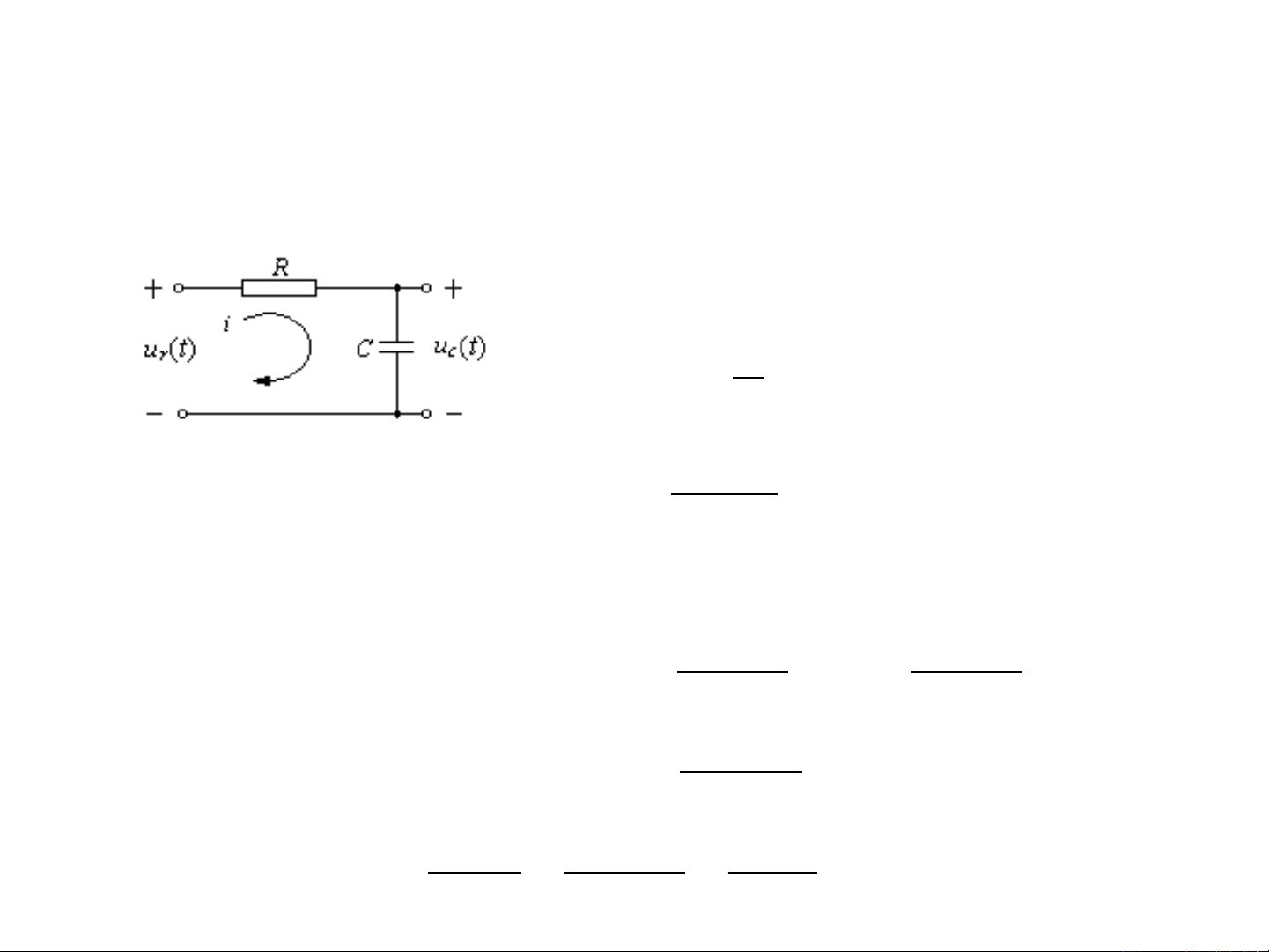 另一个例子是R-L-C电路，其中输入电压ur(t)和输出电压uc(t)之间的关系通过克希霍夫定律和电容的基本关系建立。通过消除电流i这个中间变量，可以得到描述uc(t)与ur(t)之间关系的微分方程。 这两个例子展示了如何运用解析法从基本物理定律出发建立系统的数学模型。同时，实验法也是建立模型的一种方法，它基于实际测量的输入输出数据，通过数据处理和统计分析来推断系统的数学模型，这种方法在无法直接获得物理定律或者系统过于复杂时尤为适用。 理解并掌握控制系统数学模型的构建方法是学习自动控制原理的关键，它能帮助我们预测和优化系统的性能，设计有效的控制器，以实现期望的控制目标。无论是理论推导还是实验数据处理，都是为了更好地理解和控制复杂系统的动态行为。