SVM视频教程：拉格朗日乘子与间隔最大化

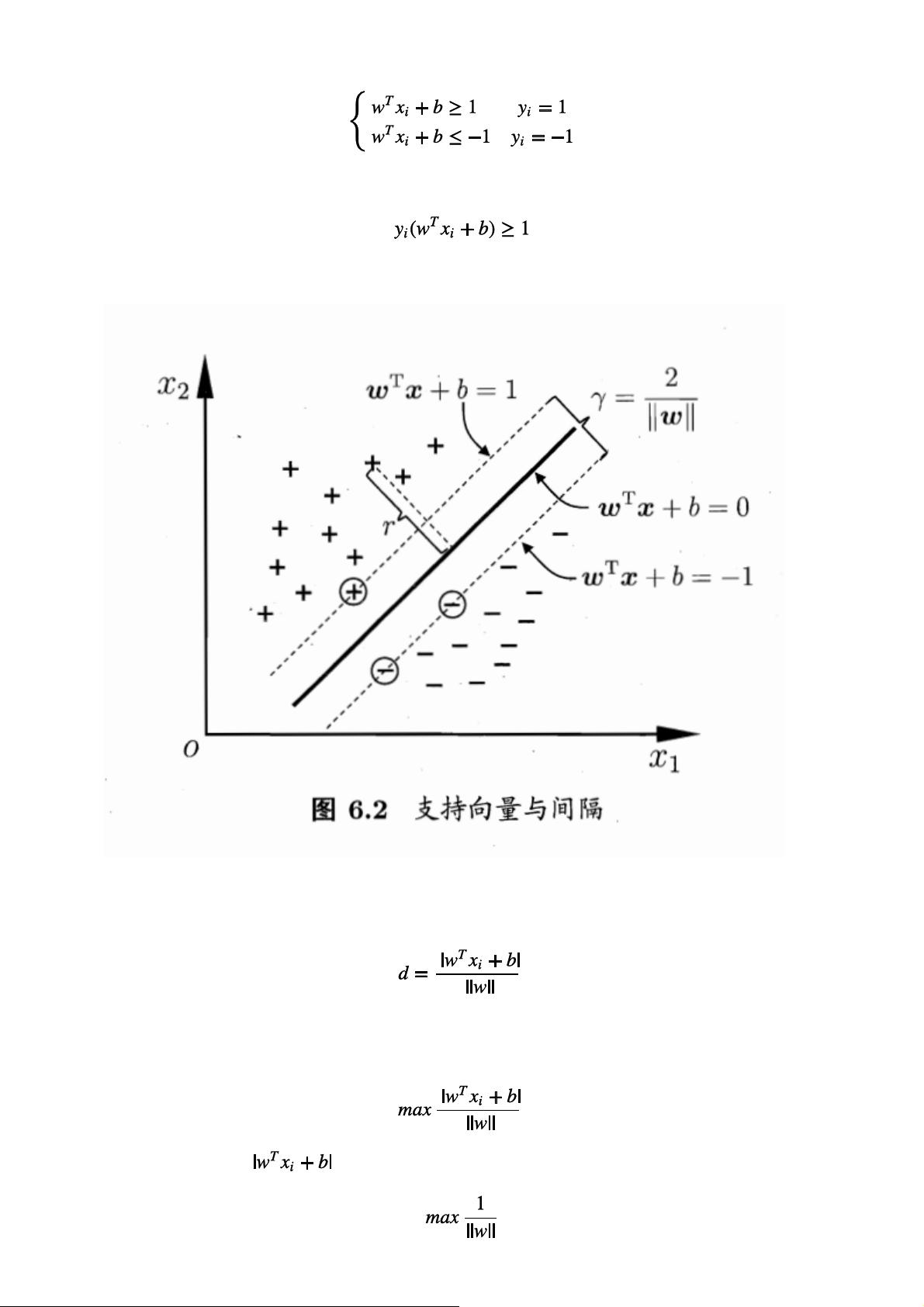
SVM视频文稿1深入讲解了支持向量机(SVM)的基本概念和优化方法。主要内容包括以下几个部分： 1. 间隔和支持向量：首先介绍了线性可分的概念，即在二维空间中，两类数据点可以用一条直线完全区分，且两边距离最大。支持向量是指那些位于分类边界的点，它们决定了分类的边界（超平面）。 2. 超平面与最大间隔超平面：超平面就是能将两类样本分开的直线或超平面，而最大间隔超平面是指使两类样本点到其两侧的距离最大化的超平面。这有助于提高模型的泛化性能。 3. SVM的最优化问题：SVM的核心目标是找到最大间隔超平面，即让所有样本点到超平面的距离之和（即间隔）尽可能大。通过数学公式，如使用核函数，将问题转化为优化距离d的形式，使得所有样本点满足d > 0，而支持向量的贡献更大。 4. 对偶问题与软间隔：为了处理线性不可分的情况，引入了对偶问题，这是一种解决原始问题的有效方式。对偶问题有助于缓解硬间隔带来的过于严格的分类要求，允许某些样本点稍微偏离分类边界，引入了惩罚项，这就是软间隔的概念。 5. 核函数：当数据非线性可分时，核函数将数据映射到高维特征空间，使得原本线性不可分的问题在高维空间变得线性可分。常见的核函数如线性核、多项式核和高斯径向基函数(RBF)核等。 6. 求解过程：使用拉格朗日乘子法和KKT条件求解优化问题，通过构造拉格朗日函数并找到其关于w和b的最小值，以及对偶问题的求解，以获得最优的分类决策边界。 通过这个视频教程，学习者可以系统地理解SVM的工作原理，从基础概念到实际应用，包括如何处理线性和非线性问题，以及对偶方法在优化中的关键作用。掌握这些内容对于理解和使用SVM进行分类任务至关重要。