贪婪方法：局部最优到全局最优的策略

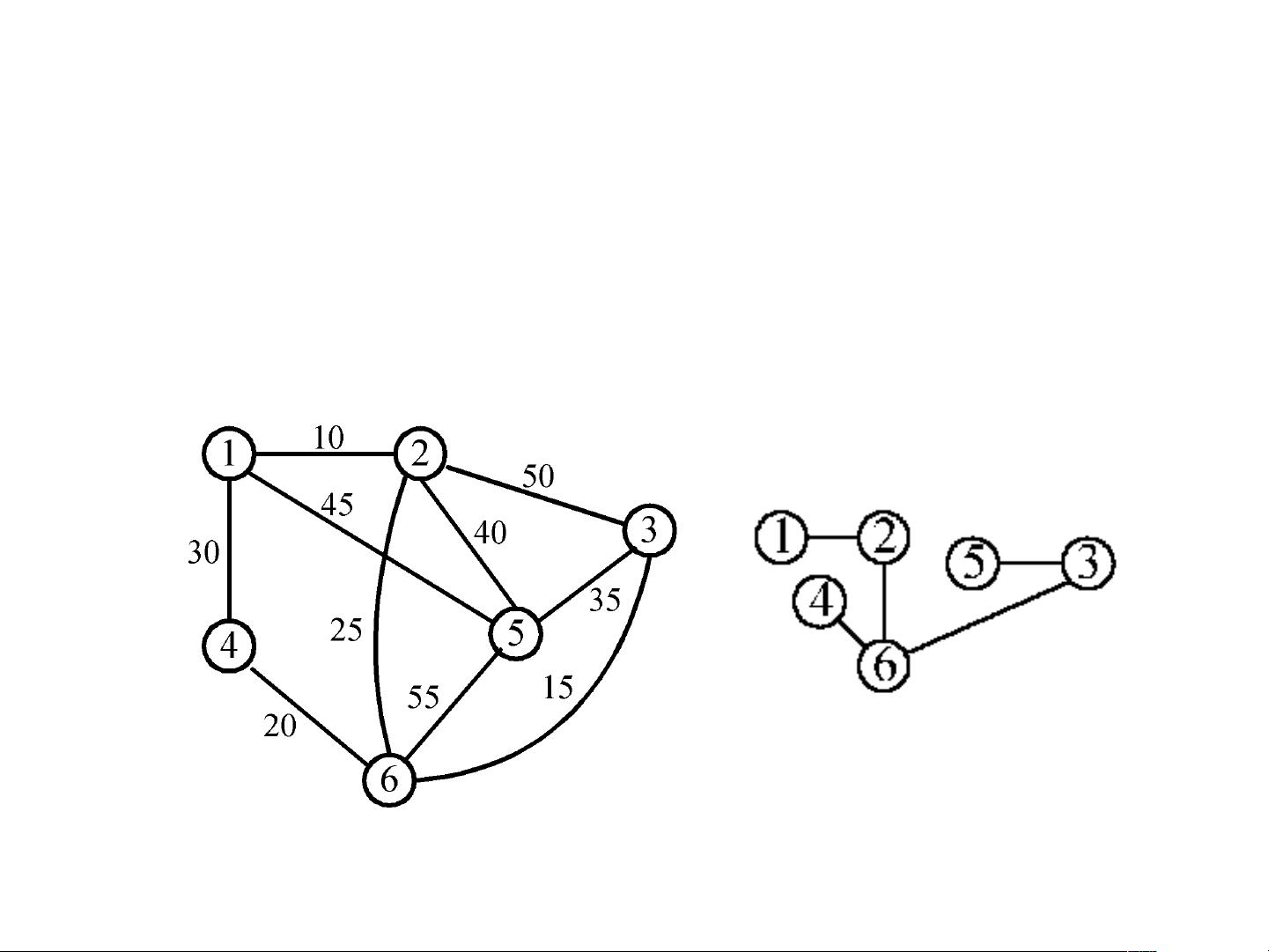
"贪婪算法是求解优化问题的一种策略，其基本思想是在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的。贪婪方法通常用于解决可以分解为一系列决策的问题，每个决策在当时看起来都是最佳的，期望这些局部最优能组合成全局最优解。然而，并非所有问题都能通过贪婪策略得到全局最优解。 以一个简单的例子来解释贪婪算法：假设有一个问题是从n个数字中选取k个，使得这k个数字之和最大。贪婪算法的解决方案是每次都选择剩余数字中最大的一个并将其从输入中删除，重复这个过程直到选够k个数字。这种方法保证了每次选择的数字都是当前剩余数字中最大的，因此能得到最大的和。 贪婪算法在某些特定的优化问题上表现良好，例如寻找图中的最短路径。如在一个特殊的图中，从顶点v0到v3的最短路径可以通过每次选择当前节点到下一节点的最小边来找到。例如，路径v0-v1-2-v3的总权重是1+2+4=7，这是最短路径。 但在多阶段图中寻找最短路径时，贪婪方法可能失效。例如，在一个图中，路径v0-v1-2-v2和1-v2-v3分别是最短路径，但将它们组合（v0-v1-2-v2, 1-v2-v3）得到的总权重是23，这不是最优解。实际的最短路径是v0-v1-1-v2-2-v3，总权重为7。在这种情况下，贪婪方法不能得出全局最优解。 为了解决上述问题，可以采用动态规划的方法。动态规划通过计算所有可能的子问题的最短距离（dmin(i,j)表示顶点i到顶点j的最小距离），然后逐步构建整个图的最短路径。对于v0到v3的最短路径，需要考虑所有可能的路径组合，找到总权重最小的那个。 总结起来，贪婪算法是一种简单而直观的策略，适用于某些优化问题，但并不总是能得到全局最优解。在遇到需要综合考虑多个决策阶段的问题时，如多阶段图的最短路径问题，可能需要采用更复杂的策略，如动态规划，以确保获得全局最优解。"