模拟退火算法深度解析与实战应用
需积分: 5 136 浏览量
更新于2024-06-13
收藏 251KB DOCX 举报
"本文详细介绍了人工智能优化技术中的模拟退火算法,包括其原理、关键参数的选择以及在实际问题中的应用。适合研究者、工程师和学生学习,以加深对模拟退火算法的理解和应用能力。"
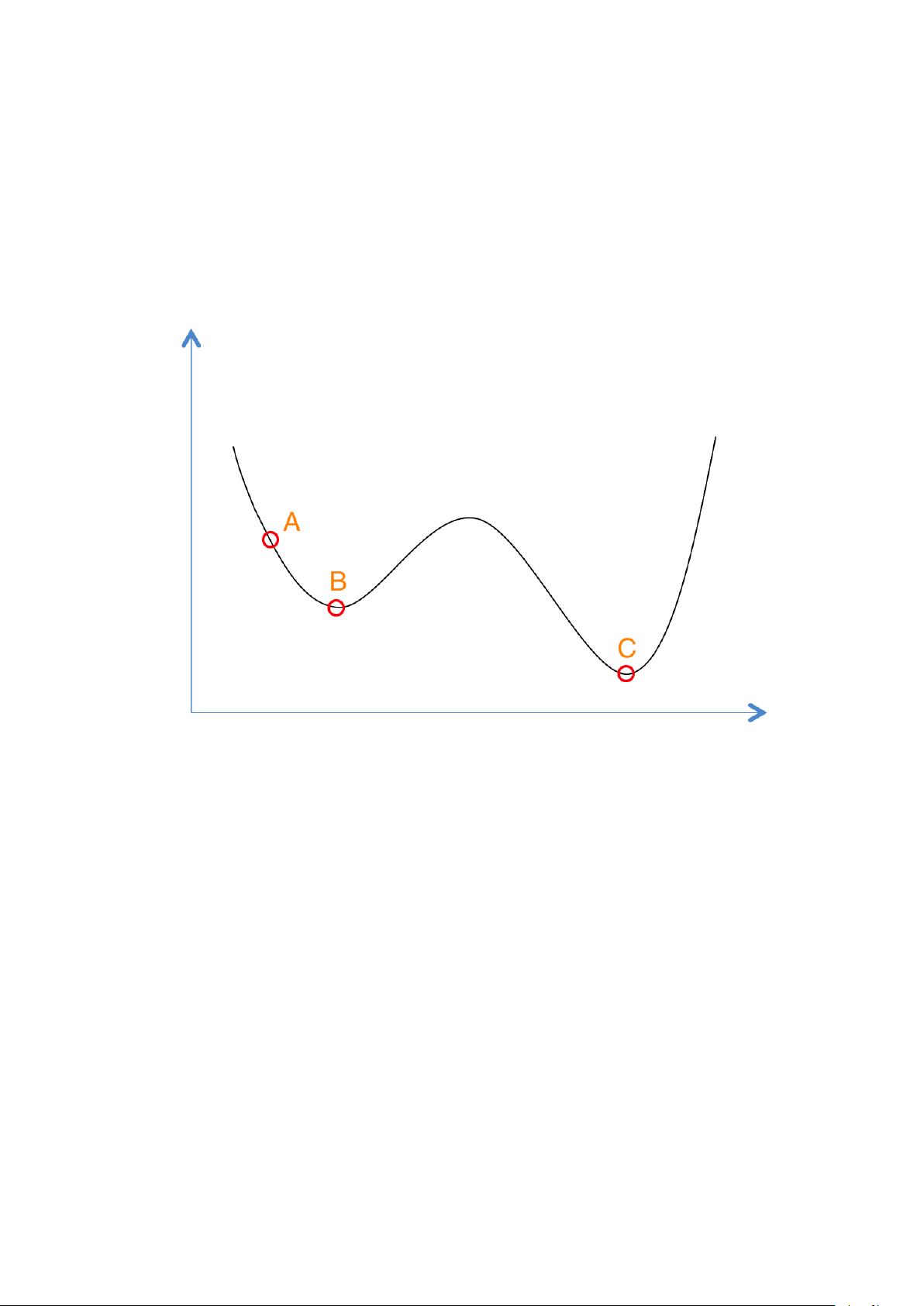
模拟退火算法是人工智能优化领域中的一种重要方法,源于固体物质退火过程的物理现象。在优化问题中,它通过模拟高温到低温的冷却过程,寻找问题的全局最优解。算法的核心在于利用概率机制避免过早陷入局部最优,从而提高找到全局最优解的可能性。
算法的运行主要包括以下几个步骤:
1. 初始化:设置初始温度T(足够高)和初始解S,以及每轮迭代的次数L,冷却进度表参数(如衰减因子Δt、每个温度下的迭代次数L和停止条件S)。
2. 迭代过程:对于每一轮迭代k,执行以下操作:
- 生成新解S',通常通过对当前解进行微小变动(如置换、互换元素)来实现。
- 计算目标函数值差Δt′ = C(S') - C(S),其中C(S)和C(S')分别表示新解和当前解的目标函数值。
- 根据Metropolis准则,如果Δt′<0,新解S'总是被接受;否则,以概率exp(-Δt′/T)接受S',这里的T是当前温度。
- 如果满足终止条件(如连续多个新解未被接受),则输出当前解作为最优解,算法结束。
- 温度T逐渐降低,然后进入下一轮迭代。
3. 冷却进度表的设定:控制参数T的衰减方式和速度,这直接影响算法的性能。合理的冷却进度表能够保证算法在不同温度阶段有足够的探索性和收敛性。
模拟退火算法的关键在于正确选择参数,如初始温度、降温速率和迭代次数。这些参数的设定需要兼顾算法的搜索广度和深度,以平衡全局搜索和局部搜索的能力。此外,新解的产生方式也会影响算法效率,应尽量选择简单且能有效探索解空间的方法。
通过学习模拟退火算法,你可以理解如何构建和调整算法参数,解决实际的组合优化问题。实践中,结合具体问题编写和调试代码,将理论知识应用于实际场景,是掌握该算法的关键。同时,实战案例的学习将帮助你更直观地理解算法工作原理,提高问题解决能力。
2023-02-27 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
望舒@
- 粉丝: 1178
- 资源: 20
最新资源
- project-
- javaStudy
- PSP Tools package-开源
- cfdi-files-ws:从 CFDI 文档生成文件的 Web 服务
- Yet Another Web Server-开源
- AMQPStorm-2.2.1-py2.py3-none-any.whl.zip
- uptimes:El Eliyar Eziz的正常运行时间监控器和状态页面,由@upptime提供支持
- Test_LDPC (2).zip
- grunt-generate-config
- VC++基于mfc71.dll渐变变色按钮
- recaptcha:适用于Laravel的Google ReCaptcha V3软件包
- 电子功用-基于IEC标准的家用电器输入功率测试方法及装置
- visual studio2022已经编译好的ceres库
- 一键部署kubernetes1.18版本
- Pomodoro
- 基于HTML的移动网页布局--携程网.zip