奈氏判据在系统稳定性分析中的应用

"本资源主要涉及自动控制理论中的奈氏判据，用于分析和判断控制系统稳定性，特别是通过开环频率特性来评估闭环系统的稳定状态。内容涵盖了传递函数的型式、开环对数幅频和相频特性渐近曲线的绘制方法、系统开环极坐标图的绘制以及奈奎斯特稳定判据的基础知识。" 在自动控制理论中，奈氏判据是一种重要的系统稳定性分析方法，尤其在工业自动化领域中有着广泛的应用。它基于复变函数理论的幅角定理，通过对系统开环传递函数的频率响应进行分析，来判断闭环系统的稳定性。首先，我们需要了解传递函数的型式，通常以时间常数来表示，这有助于我们理解系统的动态特性。 在分析系统的频率特性时，我们首先要计算各环节的转角频率及20logK的dB值，并按频率大小排序。接着，绘制开环对数幅频特性渐近曲线，从低频段开始，每经过一个转角频率，根据环节的性质改变渐近线的斜率。同时，对于相频特性，可以通过分析法计算关键点并连接成线，形成开环极坐标图，关注起点、终点和与实轴的交点，这些信息反映了系统的稳定性特征。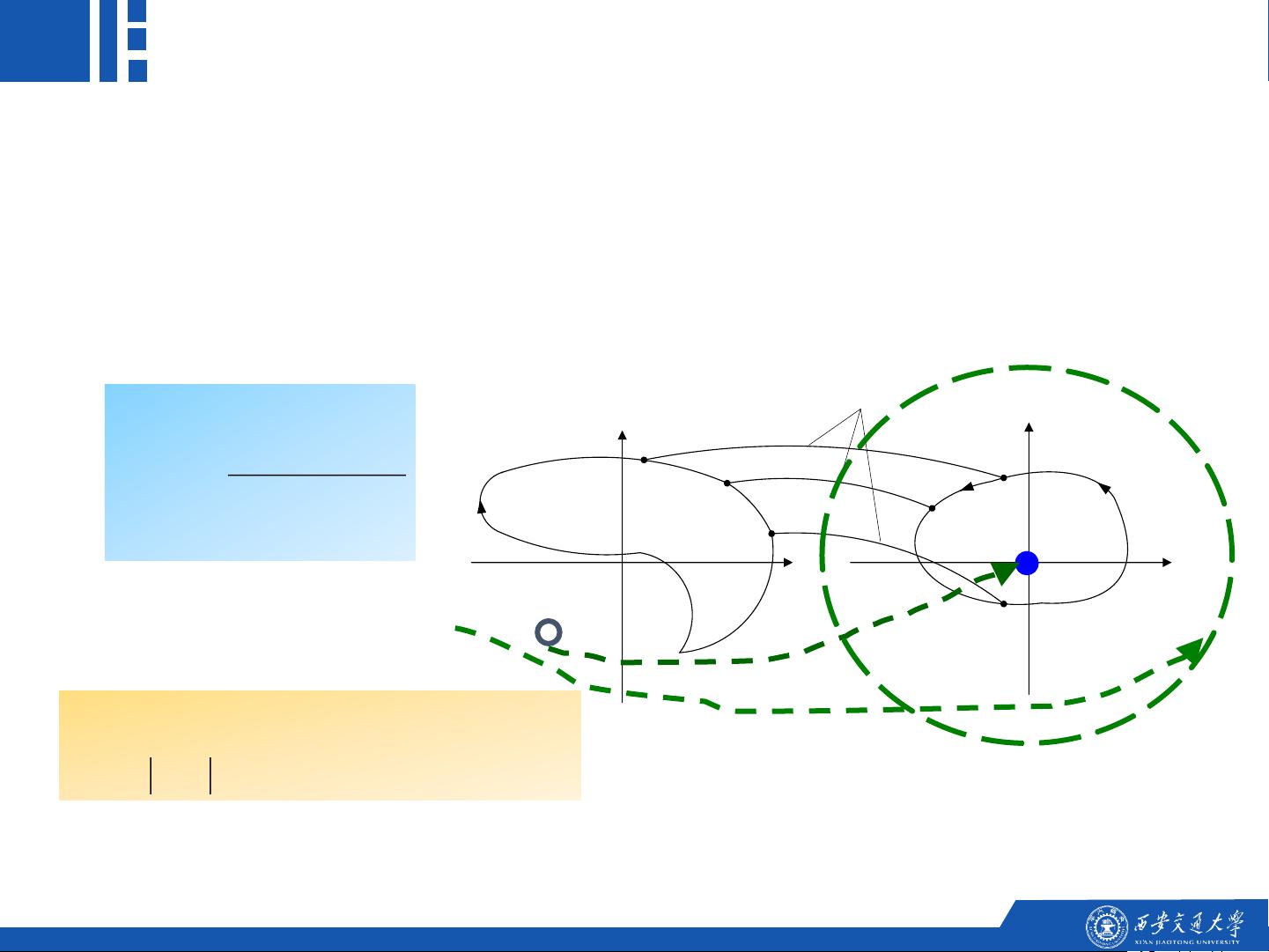 系统开环极坐标图的绘制是评估稳定性的重要步骤，包括起点（ω=0+）和终点（ω=∞）的位置，以及与实轴的交点（即开环幅相曲线的零点和极点）。此外，曲线的变化范围，如单调性和象限分布，也提供了关于系统稳定性的线索。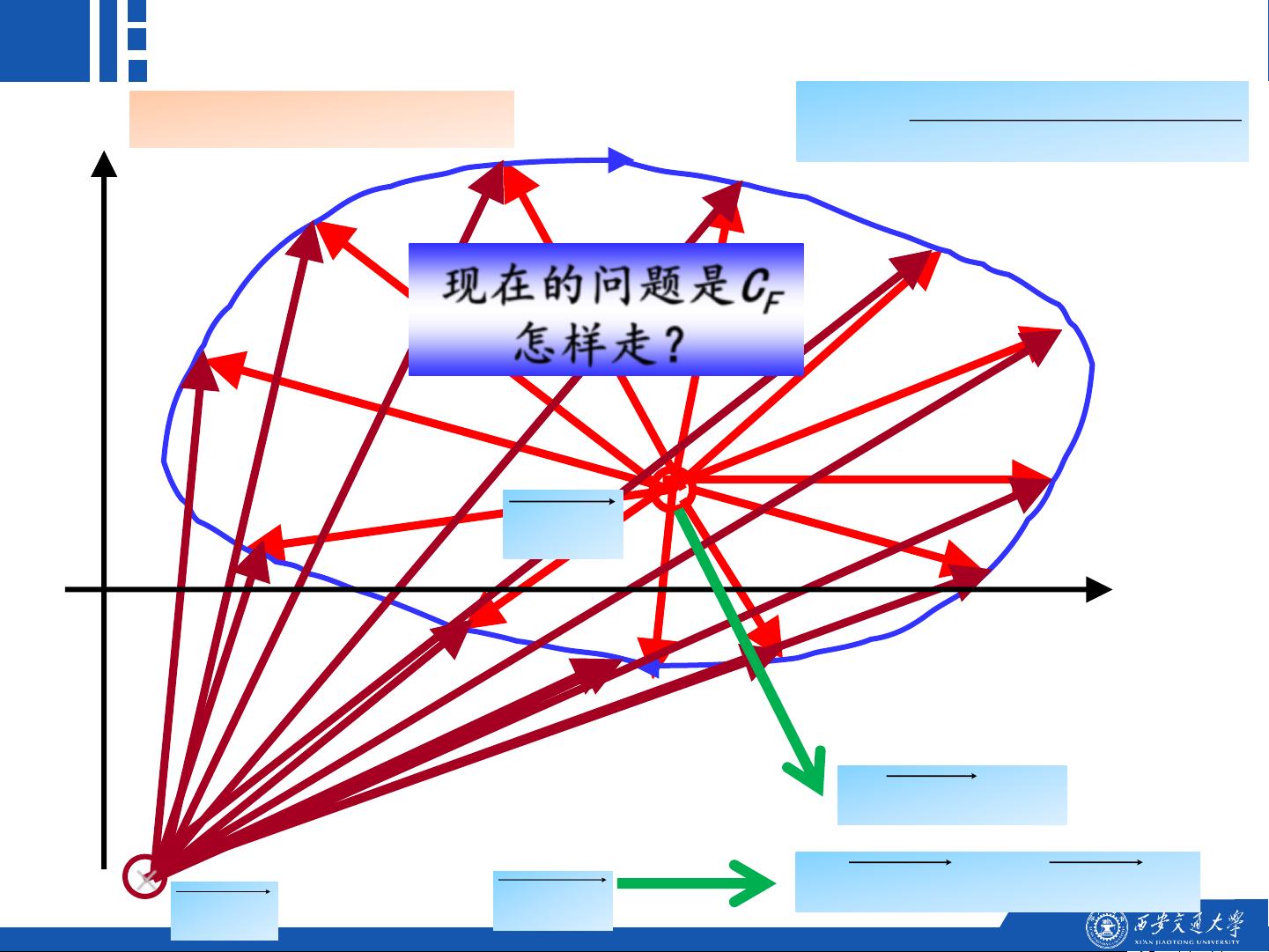 奈奎斯特稳定判据利用映射定理，将s平面上的点映射到F(s)平面上，通过对s平面特定区域的分析，可以判断闭环系统的稳定性。当s=-zj时，F(s)=0，这是判据中的一个关键点。通过这种方法，工程师不仅可以确定系统的绝对稳定性，还可以评估其稳定程度，并为不稳定系统提供改进建议，比如调整系统参数或改变系统结构以实现稳定性。 奈氏判据是控制理论中不可或缺的一部分，它为理解和改善系统的动态行为提供了有力的工具，对于控制系统的设计和优化具有重大意义。在实际工程应用中，正确运用这一判据可以确保系统的性能和稳定性，避免因系统不稳定导致的不良后果。