树状数组详解与应用：解决区间求和与修改问题

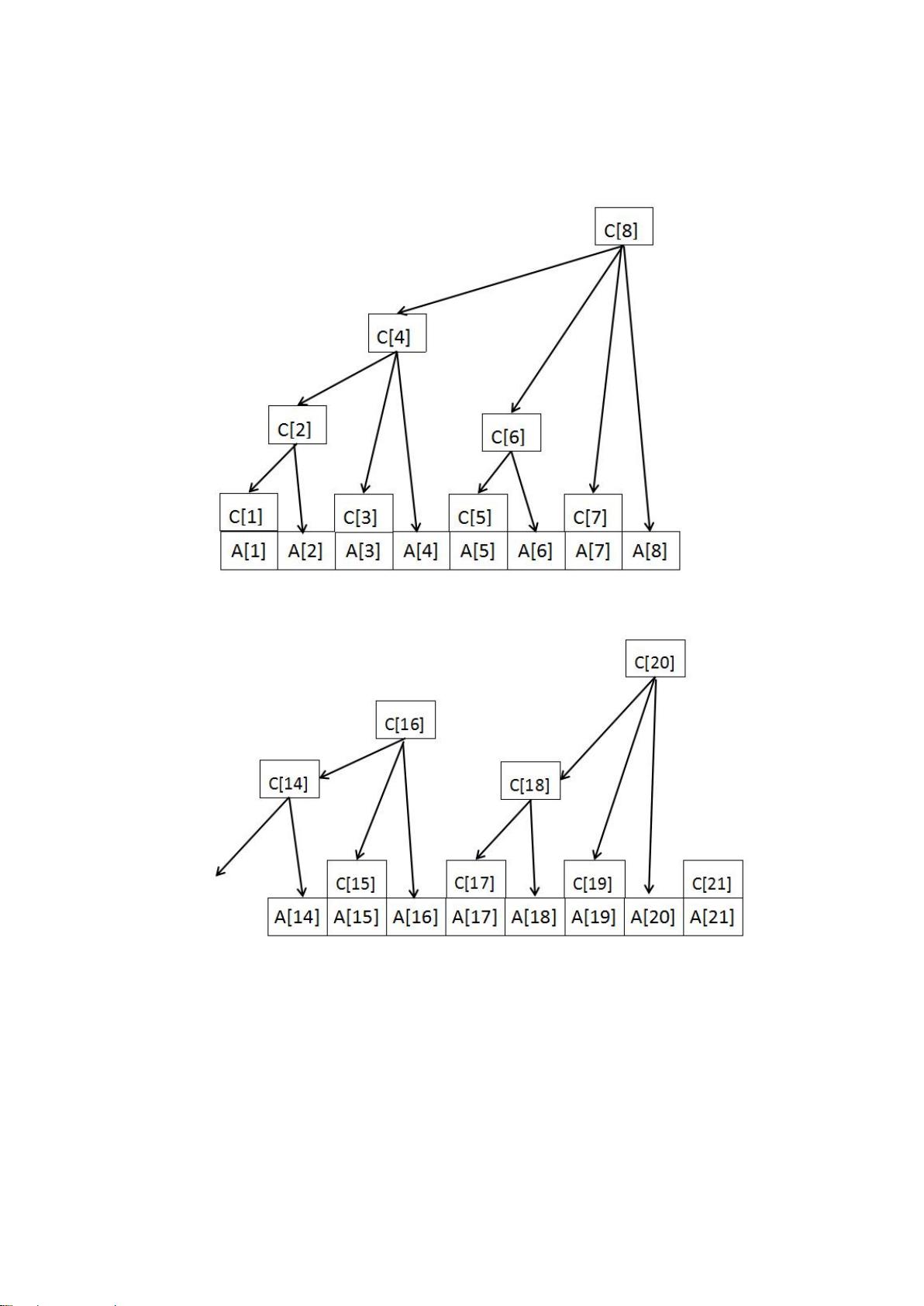
"本文详细介绍了树状数组的原理，并用树状数组解决‘校门外的树’这个问题。" 树状数组是一种高效的数据结构，主要用于处理动态维护区间和的问题，尤其适用于大规模数据的快速更新和查询。它源于数组，但通过一种特殊的方式组织数据，使其在查询和修改操作上具有较高的效率。 在算法领域，特别是在竞赛编程中，树状数组常用于解决如动态区间求和这样的问题。当需要频繁地修改数组元素并计算区间的累计和时，传统的线性遍历方法会因时间复杂度较高而导致性能不佳。树状数组通过二进制分解的特性，实现了对数组的高效更新和查询。 树状数组的基本思想是将每个元素对应的前缀和分布在数组的各个位置上，每个位置存储的是以该位置为结尾的连续子数组的和。这个数组被称为树状数组或二进制指数累加表。例如，对于一个数组A，其树状数组C[i]存储的是A中所有小于或等于i的元素的和。 在树状数组的构建过程中，每个元素i对应的值会被分到多个区间，这些区间是由i的二进制表示决定的。每个区间对应二进制表示中的一段连续的1。例如，数字21的二进制表示为10101，因此可以划分为三个区间：[1,16]、[17,20]和[21,21]，对应的区间长度分别是2^0、2^1和2^2。每个区间对应的和会存储在树状数组的特定位置上，这些位置可以通过lowbit函数来确定。lowbit函数返回一个非负整数n在二进制表示下最低位的1及其后面的0所构成的数值。 在树状数组中，进行修改操作（例如增加数组中某个位置的值）时，只需要更新与这个位置相关的所有区间和，而无需重新计算整个数组的前缀和。同样，查询一个区间和时，也可以通过一系列的查表和加法运算快速得到结果，时间复杂度为O(log N)。 在解决“校门外的树”这个问题时，树状数组可能被用来记录和更新每棵树的信息，比如树的数量、高度或其他统计信息，从而高效地处理各种查询和修改请求。例如，可以使用树状数组来快速计算某个区间内树的总数，或者统计在指定范围内高度大于某个阈值的树的数量。 树状数组是一种强大的工具，尤其适用于需要快速处理动态区间信息的问题。通过对数组的二进制分解，它能够在O(log N)的时间复杂度内完成更新和查询操作，大大提高了算法的效率。在实际应用中，树状数组常常出现在解决动态区间问题的竞赛题目中，是编程竞赛选手必备的技能之一。