从浅显分析到深入理解，揭示离散傅立叶变换的奥义

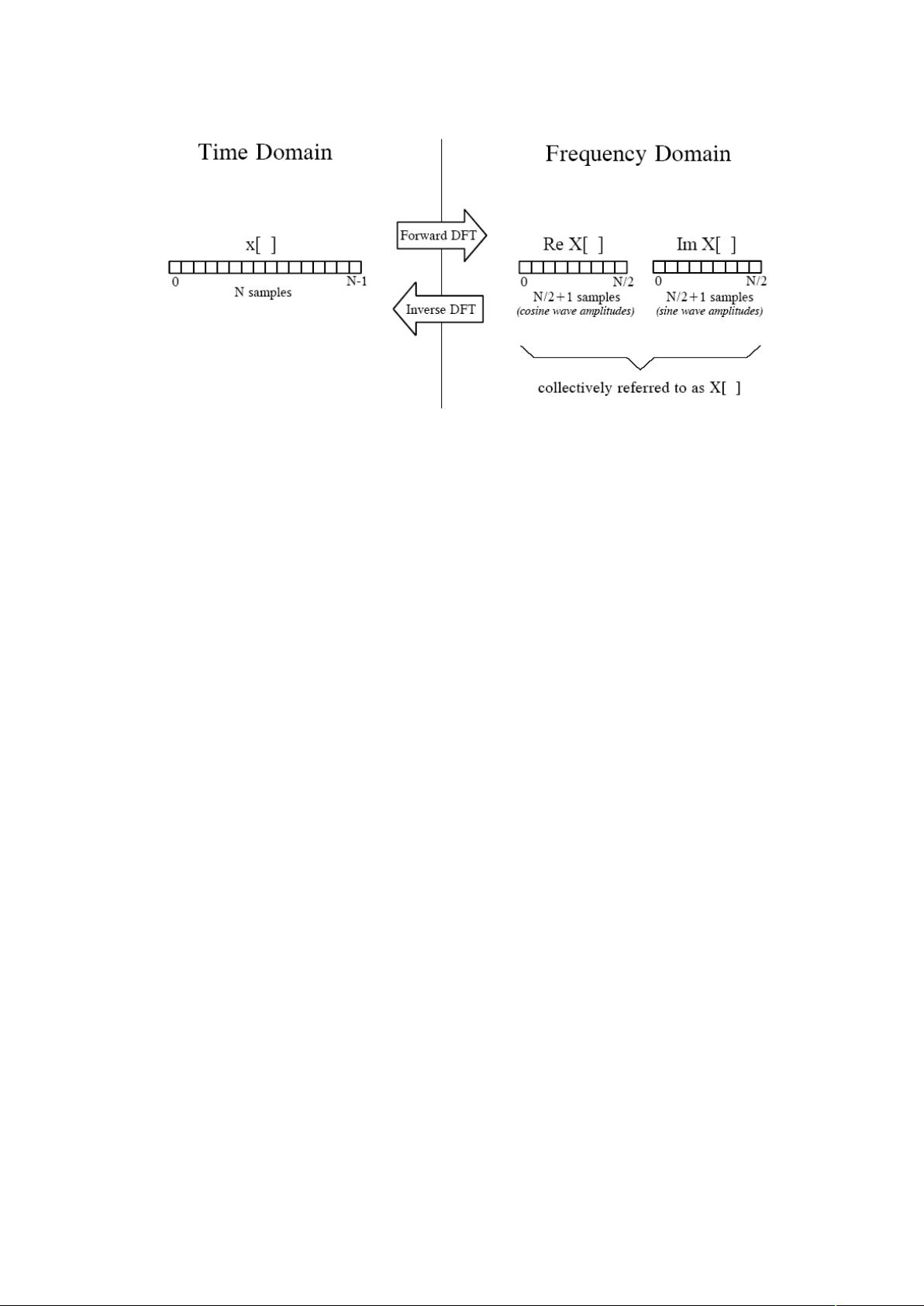
傅立叶变换是一种重要的数学工具和信号处理技术，它在各种领域有着广泛的应用，包括通信、图像处理、音频处理等。然而，对于许多人来说，理解离散傅立叶变换可能是一个具有挑战性的任务。传统的描述可能过于抽象，充斥着晦涩的公式，让人望而生畏。 最近，我偶然发现了一本非常浅显易懂的数字信号处理电子书籍，作者是Steven W. Smith, Ph.D.。这本书用通俗易懂的语言，系统地讲解了离散信号的傅立叶变换，让我茅塞顿开。在这篇总结中，我将分享我从中得到的理解，希望能给那些被傅立叶变换所迷惑的朋友们一些启发。 首先，要了解傅立叶变换，我们需要有耐心，并且具备一定的高等数学基础，尤其是级数变换。傅立叶级数变换是傅立叶变换的基础公式，而傅立叶变换则是在此基础上发展而来的。 在理解傅立叶变换的提出时，我们需要思考为什么会有傅立叶变换。傅立叶变换的产生源于对波动现象的研究，傅立叶在研究热传导过程中发现，任意一个周期信号都可以用一系列正弦和余弦函数来表示。这意味着，复杂的周期信号可以分解成简单的正弦和余弦函数的和，这样的分解为信号的频谱分析提供了数学工具。 傅立叶变换可以将一个函数在时域（或空间域）中的表达，转换成在频域中的表达。换言之，它可以将一个信号表示为频率的函数。这种变换对于处理和分析信号非常有用，比如可以对信号进行滤波、压缩或者解调。 傅立叶变换在数字信号处理中有着广泛的应用，比如在音频、图像处理中。通过傅立叶变换，我们可以将信号在频域中的信息提取出来，从而实现对信号的分析和处理。而离散傅立叶变换则是针对离散信号而提出的，它在数字信号处理领域中具有特别的重要性。 在学习离散傅立叶变换时，理解它的基本原理是非常重要的。傅立叶变换的核心思想是将信号分解成不同频率的正弦和余弦函数的组合，通过变换，我们可以得到信号在频域中的表示，从而可以更好地进行信号处理和分析。 总的来说，理解离散傅立叶变换可能需要一定的数学基础和耐心，但是通过良好的学习材料和深入的思考，我们可以掌握这一重要的数学工具和信号处理技术。希望通过我的分享，能够给那些对傅立叶变换感到困惑的朋友们一些启发。同时，我也推荐那些有兴趣的朋友可以去阅读Steven W. Smith, Ph.D.的电子书籍，相信会有很大的收获。