五一数学建模竞赛：基金配置策略的层次聚类、均值方差与动态规划分析

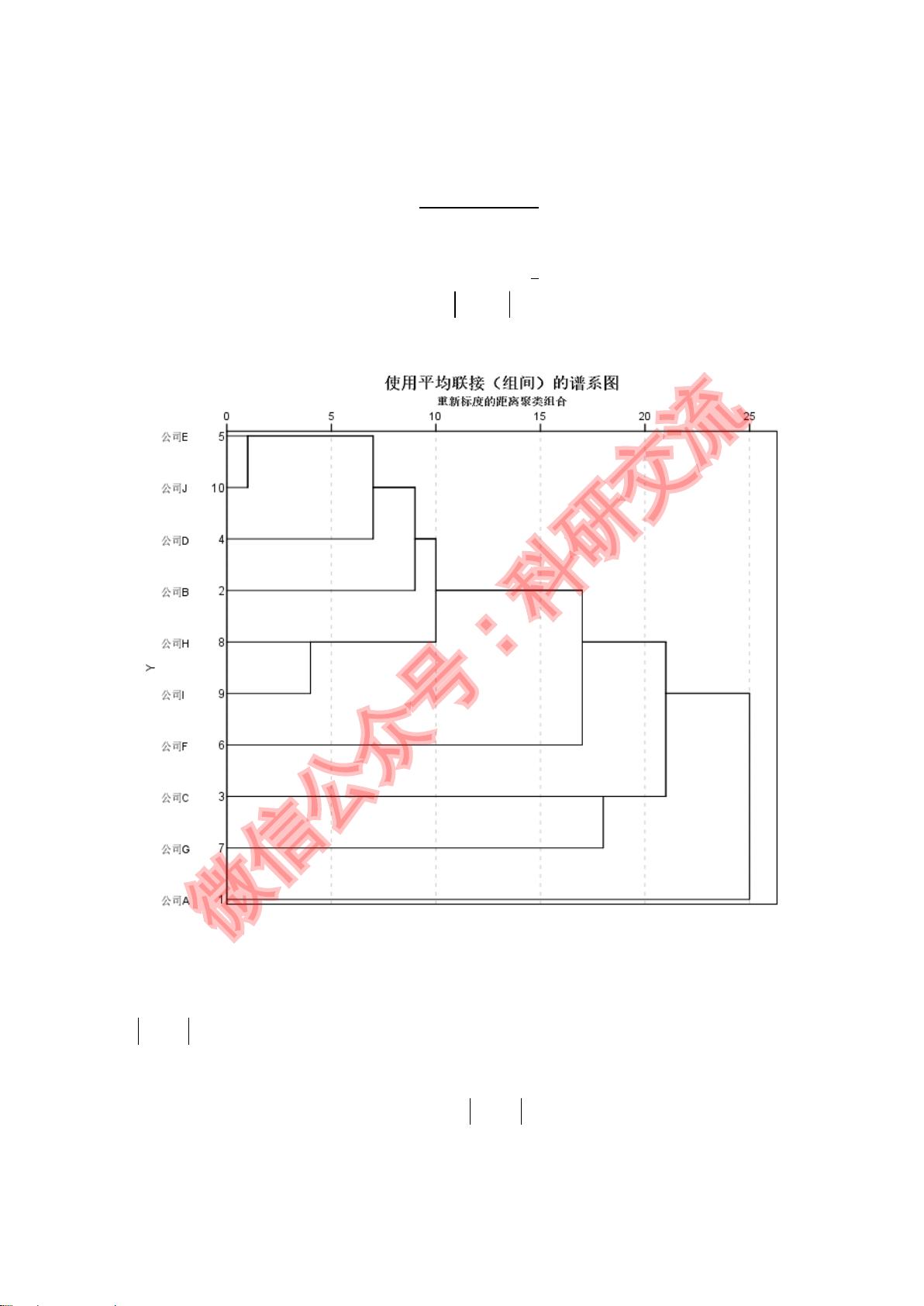
该篇论文主要讨论了在2020年五一数学建模竞赛中，关于基金资产配置策略的系统性风险角度分析。论文针对四个核心问题进行了深入研究。 首先，针对问题一，作者构建了层次聚类模型，使用SPSS软件进行数据分析，通过对10家公司的财务数据进行聚类分析，发现它们可以划分为两类：公司A、G、C、F一组，公司E、J、D、B、H、I为另一组，这表明不同的公司之间存在显著的投资组合策略相似性，有助于理解行业内部的市场特性。 问题二涉及均值-方差模型，目标是找到风险和收益的最佳平衡。通过计算协方差矩阵和执行旋转算法，论文得出在期望收益率为0.05的前提下，最优的投资组合包括股票3、7、10、22、27和41，它们分别占投资总额的7.22%、25.14%、17.46%、28.32%、6.25%和5.61%，其余股票不投资，这表明投资者应重点考虑这些高效率且相对低风险的股票。 第三部分，论文探讨了风险价值（Value at Risk，VaR）的计算，以95%的置信水平为基础，结果显示公司H的风险价值最高，达到-1075700000元，意味着其面临最大的潜在损失；而公司A的风险价值最低，为-2382100元，显示出较低的不确定性。风险价值分析对于风险管理具有实际应用价值。 最后，问题四采用动态规划模型来优化投资组合，目标函数设定为最大化期望收益的同时控制风险。通过满足特定约束条件，论文建议最优的投资策略为：公司A至J分别投资于股票5、14、12、32、14、14、45、14、55和14，展示了在不同风险偏好下，如何分配资产以实现长期稳健增长。 这篇论文提供了实用的数学模型方法，帮助参赛者理解和解决实际金融问题，特别是基金资产配置中的风险评估和优化策略，对于投资者和金融机构具有较高的参考价值。通过这些模型的应用，参赛者不仅提升了理论技能，还锻炼了解决实际商业问题的能力。