哈夫曼树与编码：数据压缩的高效工具

"本文档主要介绍了树这一数据结构，特别是哈夫曼树及其编码，这是数据压缩和通信领域的重要工具。" 在计算机科学中，树是一种非线性数据结构，它模拟了自然界中的分层关系。第十三讲主要讨论了树、森林以及哈夫曼树的概念。哈夫曼树，也被称为最优二叉树，是由美国计算机科学家David Huffman发明的一种特殊的二叉树，用于实现数据的高效编码，从而达到数据传输的最小化。 首先，路径在树中是指从一个节点到另一个节点的分支序列，而路径长度则是路径上分支的数量。树的路径长度是指从根节点到所有叶子节点的路径长度之和。在所有具有相同数量节点的二叉树中，完全二叉树拥有最小的路径长度，这是因为它的内部节点尽可能地靠近底部。 节点的权值可以根据应用场景赋予不同的数值，带权路径长度是节点的路径长度与其权值的乘积。对于一棵树，其带权路径长度（Weighted Path Length，WPL）是所有叶子节点的带权路径长度之和。构建哈夫曼树的目标就是找到一种方式，使得这棵二叉树的WPL最小。 哈夫曼编码是基于哈夫曼树的一种前缀编码方法，每个字符或符号都对应于一个唯一的二进制码，且没有哪个码是另一个码的前缀，这样可以避免在解码时产生歧义。构建哈夫曼树的过程通常涉及合并权值最小的两个节点，重复此过程直到只剩下一个节点，这个过程称为哈夫曼构建算法。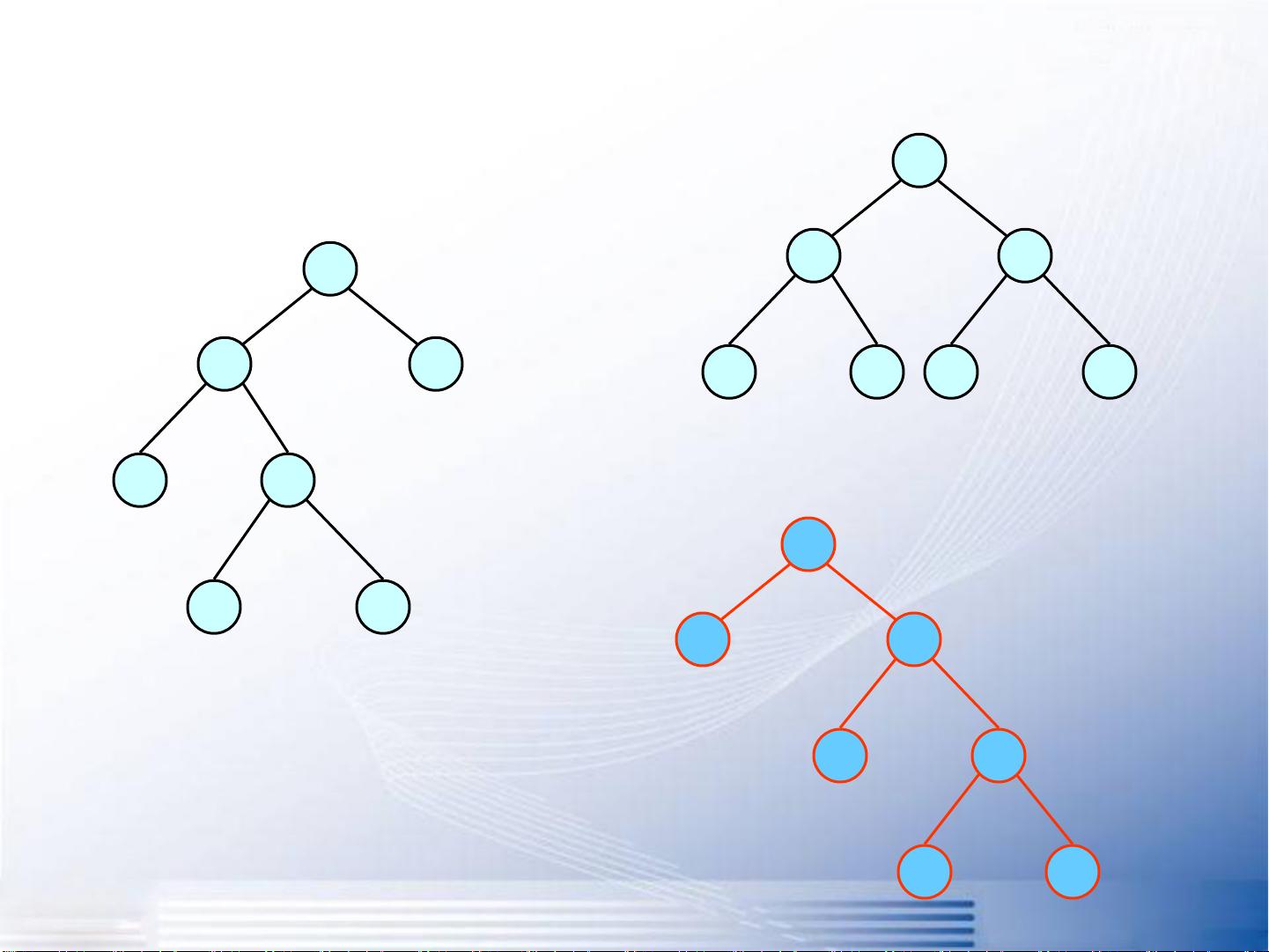 例如，给定四个节点，权值分别为7、5、2、4，可以通过不同的排列构造不同的二叉树，但目标是找到使得WPL最小的那棵树。在示例中，最后一棵展示的哈夫曼树（d->c->a->root 和 d->b->root）具有最小的WPL，为35。 哈夫曼编码的实用价值在于数据压缩，例如在图像和文本压缩中，频繁出现的字符会得到较短的编码，不常出现的字符则编码较长。这种编码方式可以显著减少数据传输量，提高传输效率。此外，哈夫曼编码也在网络通信、文件存储和解压缩等领域有着广泛应用。 总结来说，哈夫曼树和哈夫曼编码是计算机科学中数据结构和算法的重要组成部分，它们提供了一种优化数据表示和传输的方法，对于理解和实现高效的信息处理系统至关重要。了解并掌握这些概念，对于任何从事计算机科学或相关领域的专业人士都是必不可少的。