MATLAB模拟混沌系统：6个关键模型的探索与理解

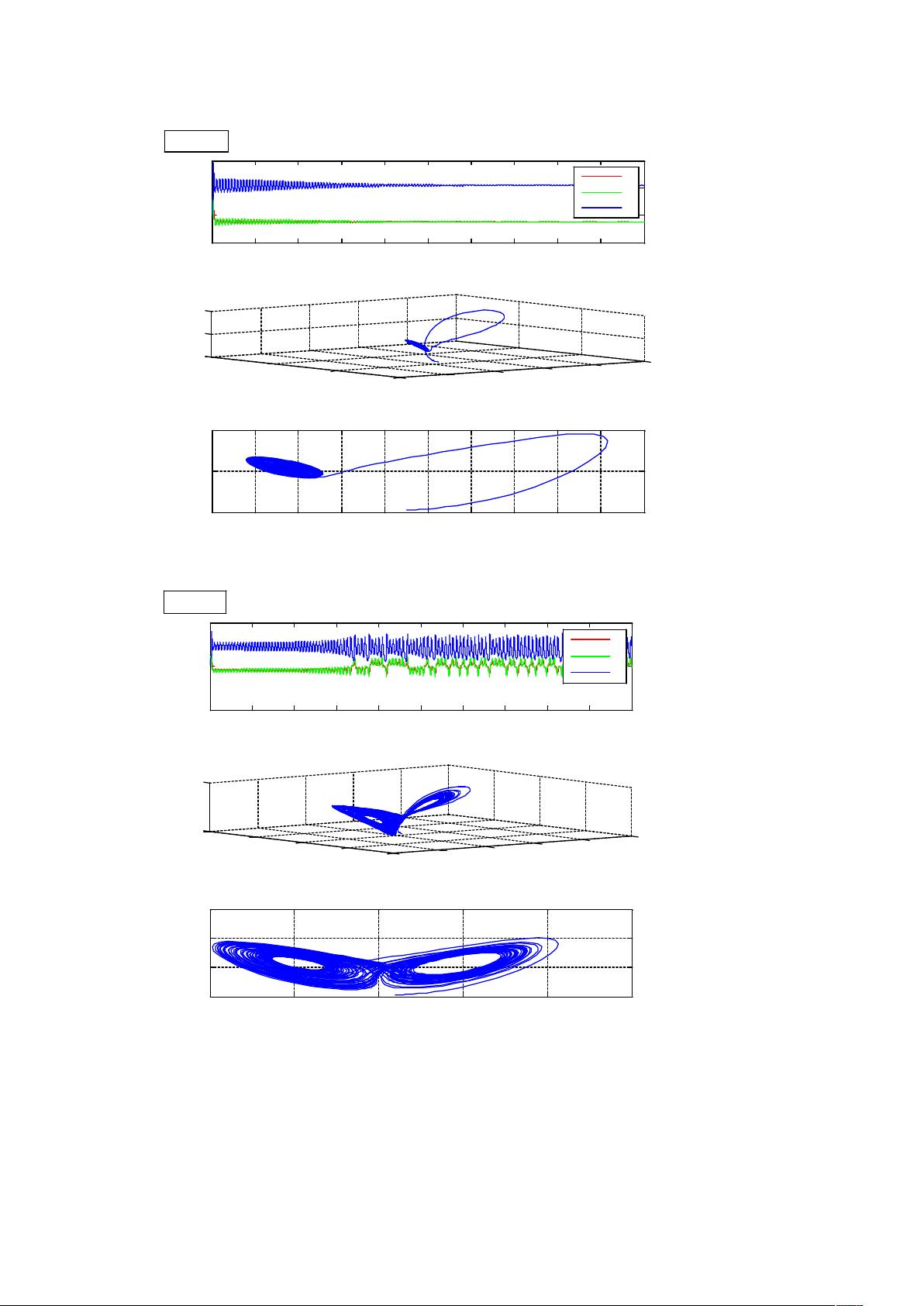
《基于MATLAB的各类混沌系统的计算机模拟》是一篇针对混沌现象研究的实用教程，由物电05级1A班学生张丹伟撰写，着重介绍了如何利用MATLAB这个强大的数学软件工具对Lorenz系统以及其他五个关键混沌模型进行数值计算和模拟。该报告旨在帮助读者理解混沌系统的基本特性和行为，包括混沌吸引子、倍周期性、初值敏感性、相图以及分岔图等。 混沌是数学和物理学中的一个重要概念，非线性系统中的复杂、不可预测的行为，如洛伦兹 attractor（Lorenz attractor）所示，即使是微小的初始条件变化也能导致长期行为的巨大差异，这就是著名的“蝴蝶效应”。在MATLAB的平台上，作者展示了如何通过编程实现这些混沌系统的模拟，使理论知识可视化，便于教学和研究。 报告的核心内容包括： 1. **混沌的基本概念**：混沌运动并非随机，而是由确定性方程产生的看似随机的运动，其特点是轨道高度不稳定，即相邻轨道会随着时间呈指数级分离。混沌的描述需要借助相空间，即用一组微分方程描述动态过程，状态变量构成系统的运动轨迹。 2. **MATLAB的应用**：MATLAB在此过程中发挥关键作用，作为数值计算和可视化工具，它提供了丰富的函数库和图形界面，使得复杂的混沌系统分析变得直观易懂。书中包含了20个实例，覆盖了从理论到实践的各个环节，对于教学和学习者来说极具实用性。 3. **具体模型分析**：报告详述了Lorenz系统等模型的模拟过程，通过观察混沌吸引子、相图和分岔图，读者可以深入理解混沌现象的特性，如吸引子的形状、周期性行为的变化以及初始值对结果的显著影响。 4. **分形与分维**：混沌系统通常具有分形特性，即在不同尺度下展现出多尺度的复杂结构。通过MATLAB，可以计算这些系统的分维数，进一步揭示其几何和动力学特性。 总结而言，《基于MATLAB的各类混沌系统的计算机模拟》不仅提供了一种教学方法，也是一项科学研究的有效工具，它结合了理论知识与实践经验，为理解和探索混沌世界的复杂性开辟了新的途径。对于任何对混沌理论感兴趣，或是希望掌握MATLAB在非线性动力学分析中的应用的人来说，这是一本不可或缺的参考资料。