线性插值算法详解：简单形式与应用

"这篇资料主要介绍了线性差值算法，它是代数插值的最简单形式，常用于软件编程中的数据逼近和函数估计。线性插值的主要思想是通过两点确定一条直线，以此来近似代替函数曲线。" 在数学和计算机科学中，线性差值算法是一种基本的插值方法，特别是在处理连续函数的数据点时非常有用。它假设给定了一条未知函数\( f(x) \)的两个点\((x_0, y_0)\)和\((x_1, y_1)\)，目标是找到一个线性函数\( g(x) = ax + b \)使得\( g(x) \)在这些点上与\( f(x) \)的值相匹配。在线性插值中，我们通常用直线来近似曲线，因为直线是最简单的几何形状，计算起来也相对简便。 线性插值的公式可以通过以下两种方式表达： 1. **点斜式**: \( g(x) = y_0 + \frac{(x - x_0)}{(x_1 - x_0)}(y_1 - y_0) \) 这个公式利用了直线的斜率和经过的两个点来定义直线。斜率由两点决定，即\(\frac{(y_1 - y_0)}{(x_1 - x_0)}\)，而\( y_0 \)是直线与\( x \)轴交点的纵坐标。 2. **两点式**: \( g(x) = \frac{(x - x_1)}{(x_0 - x_1)}y_0 + \frac{(x - x_0)}{(x_1 - x_0)}y_1 \) 这种表达方式是基于两点之间的比例关系来定义直线的。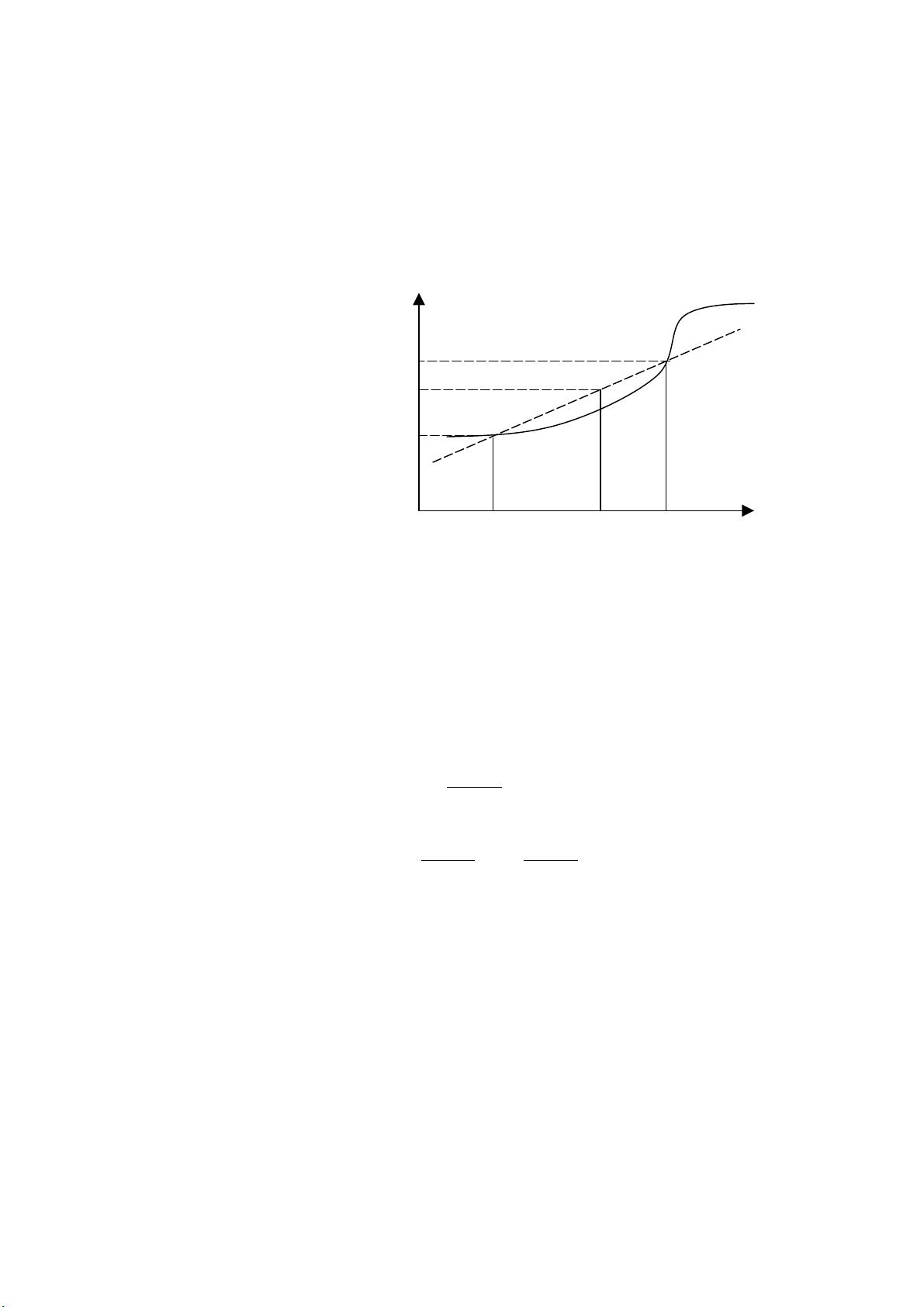 线性插值的几何意义是，它用通过点\((x_0, y_0)\)和\((x_1, y_1)\)的直线近似地代替了曲线\( f(x) \)。当插值节点间的距离越小，直线与曲线的误差也就越小。如果插值点位于两个已知点之间，我们称之为内插；否则，如果位于已知点之外，就称为外插或外推。 在实际应用中，如单片机编程，线性插值常被用来处理非线性函数，例如温度补偿值的计算，或者等间距角度的正弦函数值。在进行插值运算前，我们需要选择合适的插值节点，并将数据转换为浮点数以提高精度。浮点运算通常比整数运算更精确，但同时也需要更多的计算资源。 对于给定的插值点\( (x, z) \)，我们可以使用线性插值来估算对应的函数值。在点斜式线性插值算法中，首先将数据规格化为浮点数，然后利用点斜式公式进行计算。这样，我们就可以在任何两个已知点之间找到一个近似的函数值。 总结来说，线性差值算法是一种实用的工具，它能够有效地在有限的数据点之间构建连续的函数近似，广泛应用于各种科学计算、数据拟合和工程应用中。尽管它在某些复杂情况下可能不够精确，但对于许多实际问题，线性插值已经足够满足需求。