优化宽表布局：列顺序与重复策略
54 浏览量
更新于2024-07-14
收藏 1.58MB PDF 举报
"基于列顺序和重复的宽表布局优化"
这篇研究论文主要探讨了在大数据分析背景下，如何通过优化列顺序和重复来提升宽表（Wide Table）在存储和查询性能上的表现。宽表通常拥有几百到几千列，是数据分析任务中的常见数据结构。虽然列存储（Column Store）被认为是处理宽表和分析工作负载的理想数据格式，但论文指出，列的物理顺序对I/O性能的影响尚未得到充分研究。
论文中提到，列的顺序至关重要，因为在宽表中访问单个水平分区的列可能涉及到多次磁盘寻道。理想的列顺序可以最小化一系列查询应用到数据时的累积磁盘寻道成本，从而最大化I/O性能。为此，作者们专注于研究列存储在HDFS（Hadoop Distributed File System）上的两个问题：列顺序优化和列重复。
列顺序优化（Column Ordering）旨在寻找一种最优的列排列方式，以降低I/O操作的成本。通过对列的不同顺序进行排列组合，可以找到一个能够最小化磁盘寻道总数的排列，从而提高数据读取速度和查询效率。
另一方面，列重复（Column Duplication）是指在特定条件下复制某些列以减少I/O。这可能是为了减少跨磁盘的访问，或者是为了在查询中频繁使用的列上提供更快的本地访问。通过智能地选择和复制关键列，可以进一步优化I/O性能，尤其是在分布式环境中，如HDFS，其中网络延迟可能成为性能瓶颈。
论文的贡献在于提出了新的优化策略，并通过实验验证了这些策略在实际场景中的效果。作者们可能采用了数学模型和算法来解决这两个问题，比如使用贪心算法或动态规划来寻找最佳列顺序，以及基于数据访问模式和存储成本的分析来决定哪些列应该被复制。
这篇论文对于大数据分析和数据库系统领域的从业者具有重要的参考价值，它提供了关于如何通过列顺序和重复来优化宽表布局的具体方法，以提升整体的系统性能。这些优化技术对于处理大规模数据集和复杂查询的工作负载尤其有用，能够有效减少计算资源的消耗，提高数据分析的速度和效率。
Algorithm 1: SCOA
Input: The set of queries Q = {q
1
, q
2
, ..., q
m
};
The initial column order S
0
= {c
1
, c
2
, ..., c
n
}
Output: The optimized column order S;
1 S := S
0
, e := Cost(Q, S
0
), t := t
0
;
2 for k := 1 to k
max
do
3 t := T emperature(t, cooling_rate);
4 S
0
:= Neighbor(S);
5 e
0
:= Cost(Q, S
0
);
6 if (e
0
< e)||(exp((e − e
0
)/t) > random(0, 1)) then
7 S := S
0
;
8 e := e
0
;
9 return S;
proposed in [35]. The Temperature function is the core function of
the annealing schedule. In this algorithm, the temperature shrinks at
a rate of
(1 − cooling_rate)
. Function Neighbor(S) is to generate
a candidate neighboring state from the current state
S
, achieved
by swapping the positions of two randomly picked columns in
S
.
1
Parameter settings of SCOA are discussed in Appendix C.
3.3 Incremental Computation of Seek Cost
When the access pattern of a query follows the global column
order (as adopted by existing systems such as HDFS), we can incre-
mentally compute the seek cost of a query to speed up SCOA, given
that a neighboring state
S
0
is derived from the current state
S
by
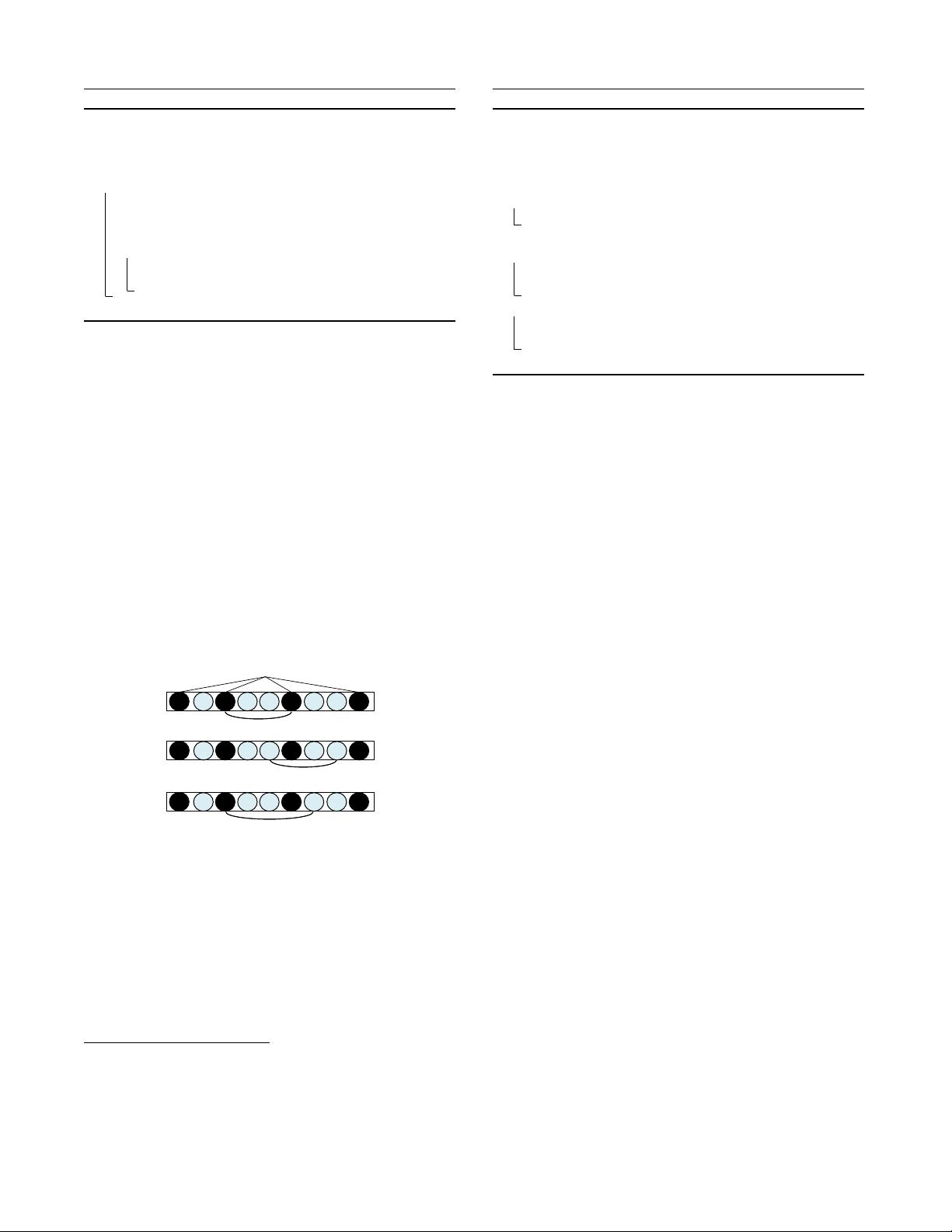
randomly swapping two columns. Consider the example in Figure 2.
Query
q
accesses 4 columns
C
q
= {c
4
, c
2
, c
6
, c
8
}
. When deriving
a new state by swapping two columns in
C
q
(e.g.,
c
2
and
c
6
in
Figure 2(a)), the seek cost of this query clearly remains unchanged
(both equal to
f(s(c
5
)) + f(s(c
1
) + s(c
3
)) + f(s(c
7
) + s(c
9
))
,
for reading a row group).
c
2
c
1
c
6
c
9
c
8
c
4
c
5
c
3
c
7
q
(a) Swap c
2
and c
6
(b) Swap c
3
and c
9
c
2
c
1
c
6
c
9
c
8
c
4
c
5
c
3
c
7
(c) Swap c
2
and c
7
c
2
c
1
c
6
c
9
c
8
c
4
c
5
c
3
c
7
Figure 2: Three cases of the delta query cost
A more complex case occurs when neither of the two swapped
columns is accessed by the query
q
(e.g.,
c
3
and
c
9
in Figure 2(b)).
The pseudo code for handling this case is presented in Algorithm 2.
The
SeekCost2ndCase
function takes as input the current state
S
and two swapped columns
c
x
and
c
y
, and outputs the seek cost of
the neighboring state
S
0
for
q
. Let
suc(c
i
)
be the first succeeding
column of
c
i
in
C
q
, and
pre(c
i
)
be first preceding column of
c
i
in
C
q
. For example, in Figure 2,
suc(c
1
) = c
6
and
pre(c
1
) = c
2
.
According to Algorithm 2, it is clear that
Cost(q, S
0
) = Cost(q, S)
if
suc(c
x
) = suc(c
y
)
. Otherwise, at most two terms in Equation 2
1
We have also tested various other neighboring state selection heuris-
tics, including substantially more complicated ones. However, none
of them outperformed the simple ‘column-swap’ heuristic. For the
sake of simplicity, we thus limit ourselves to the presentation of this
most basic version of the algorithm.
Algorithm 2: SeekCost2ndCase
Input: A query q and sorted set C
q
;
Current column order S, and its seek cost Cost(q, S);
Two swapped columns, c
x
/∈ C
q
and c
y
/∈ C
q
.
Output: The seek cost of the neighboring state S
0
,
Cost(q, S
0
)
1 if suc(c
x
) = suc(c
y
) then
2 return Cost(q, S);
3 delta := 0;
4 if pre(c
x
) 6= null and suc(c
x
) 6= null then
5 delta −= f (b(suc(c
x
)) − e(pre(c
x
)));
6 delta += f(b(suc(c
x
)) − e(pre(c
x
)) − s(c
x
) + s(c
y
))
;
7 if pre(c
y
) 6= null and suc(c
y
) 6= null then
8 delta −= f (b(suc(c
y
)) − e(pre(c
y
)));
9 delta += f (b(suc(c
y
)) − e(pre(c
y
)) − s(c
y
) + s(c
x
));
10 return Cost(q, S) + delta;
will be affected and it will be updated according to Lines 4-6 and
Lines 7-9, respectively.
The last case occurs when exactly one swapped column is ac-
cessed by
q
(e.g. Figure 2(c)), which can be handled in a similar
way to Algorithm 2. An important difference from the previous two
cases is that
C
q
will be updated if the SA algorithm accepts this
neighboring state S
0
.
Time Complexity.
To maintain the sorted set
C
q
efficiently,
we use a binary balanced search tree to insert, remove and query
preceding and succeeding elements. All these operations run in
O(log R)
time. The overall time complexity of computing seek
costs is
O(|Q|· log R)
, where
R
is the average number of columns
accessed by a query. Compared to the naive approach of sorting all
the columns for every new ordering, this incremental approach is
R
times faster. On the production data we tested,
R
is 32 and SCOA
with incremental seek cost computation only requires a few minutes
to converge.
Besides simulated annealing (SA), we have tried several other
meta heuristics. Particularly, we have also tried to apply genetic
algorithm (GA) [37, 51] in Appendix D and AutoPart [41] algorithm
in Appendix E. Results show that SA performs much better.
4. STORAGE CONSTRAINED COLUMN DU-
PLICATION
Suppose we have extra storage headroom, we may be able to
further reduce the overall seek cost by duplicating some popular
columns and inserting them into carefully selected positions within
the derived column orders. Consider the simple example in Figure
3. In Fig. 3(a), the seek cost of both
q
1
and
q
2
is 0 while the seek
cost of
q
3
is
f(s(c
3
) + s(c
6
))
(Note that the initial seek cost
can
be ignored as it is constant). In Fig. 3(b), however, if we duplicate
c
1
, insert it between
c
6
and
c
7
, and let
q
3
access the new replica of
c
1
, the seek cost of all three queries becomes 0.
We formally define the column duplication problem as follows.
DEFINITION 7 (COLUMN DUPLICATION PROBLEM).
Given a workload
Q
and the storage headroom
H
, identify a set of
duplicated columns with an ordering strategy
S
D
such that 1) the
total size of duplicated columns is not greater than
H
and 2) the
seek cost of Q is minimized.
In this section, we first introduce the basic idea of the duplication
process in Section 4.1 and then provide details of how to optimize it
in Section 4.2.
剩余15页未读，继续阅读
2024-05-18 上传
2022-05-06 上传
2011-07-08 上传
2023-03-27 上传
2023-05-26 上传
2023-05-31 上传
2023-04-25 上传
2023-03-25 上传
2023-09-09 上传
weixin_38654315
- 粉丝: 5
- 资源: 962
我的内容管理
展开
