图像处理中的矩阵基础与SVD应用：K-means聚类实例

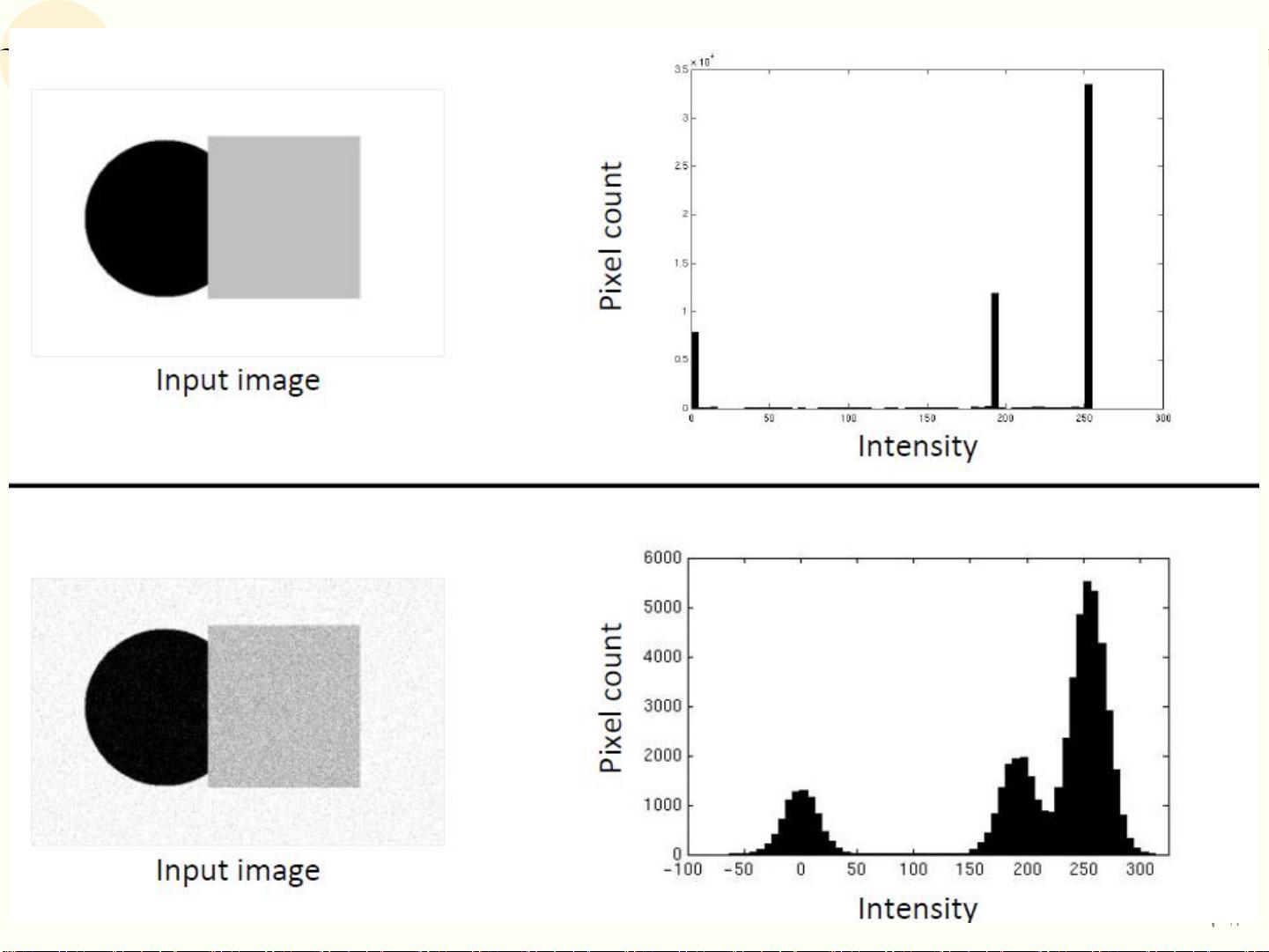
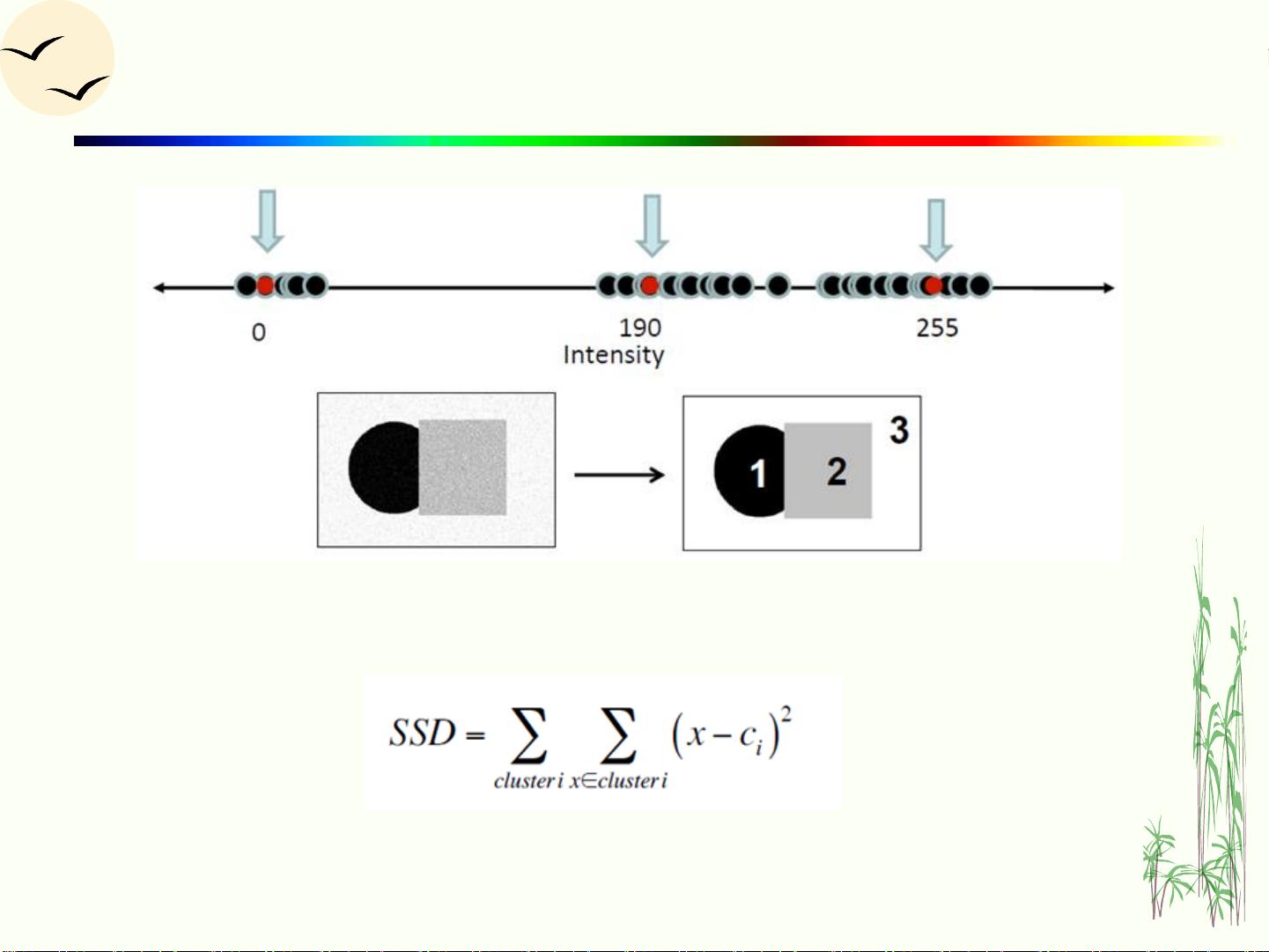
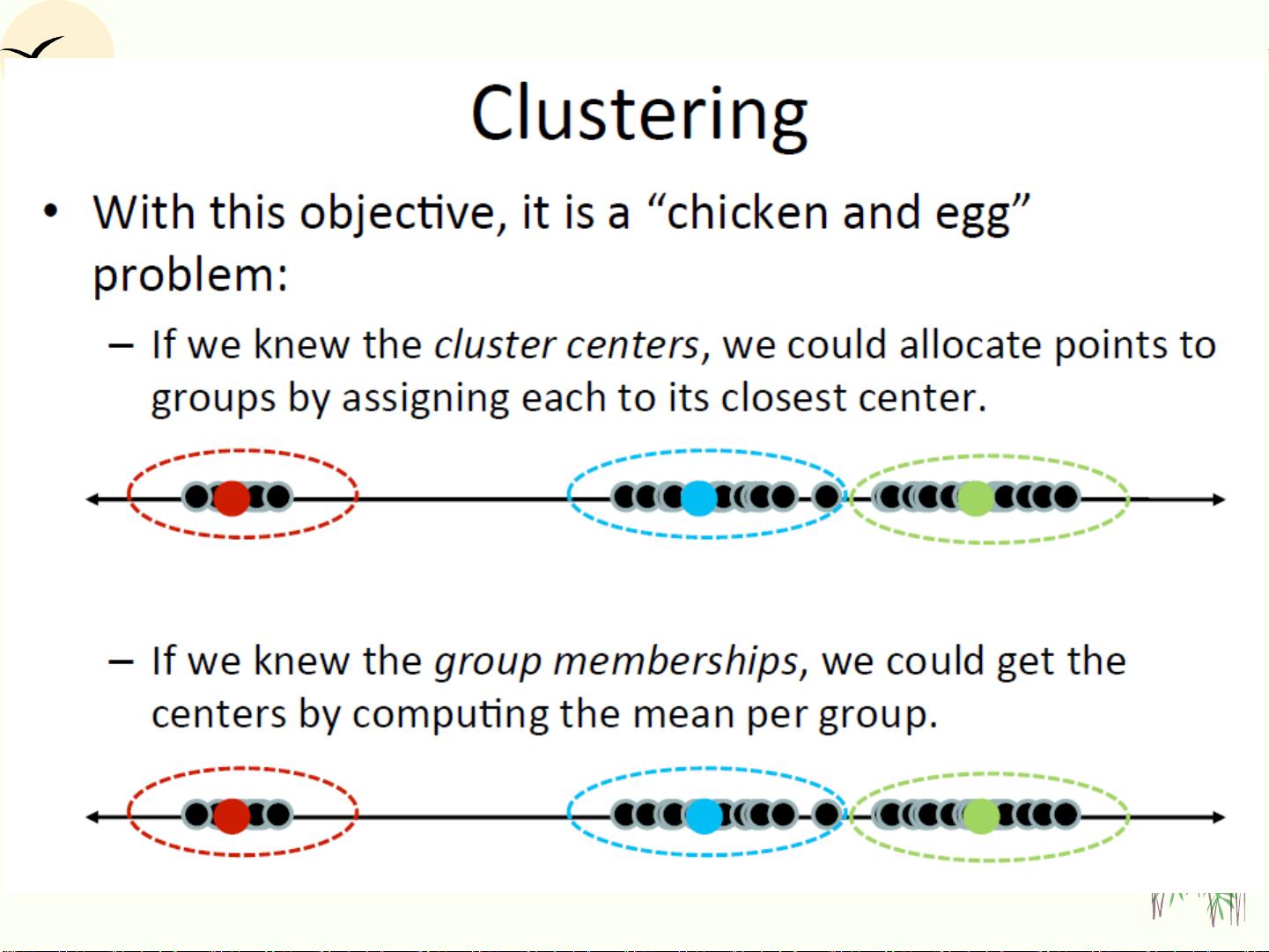
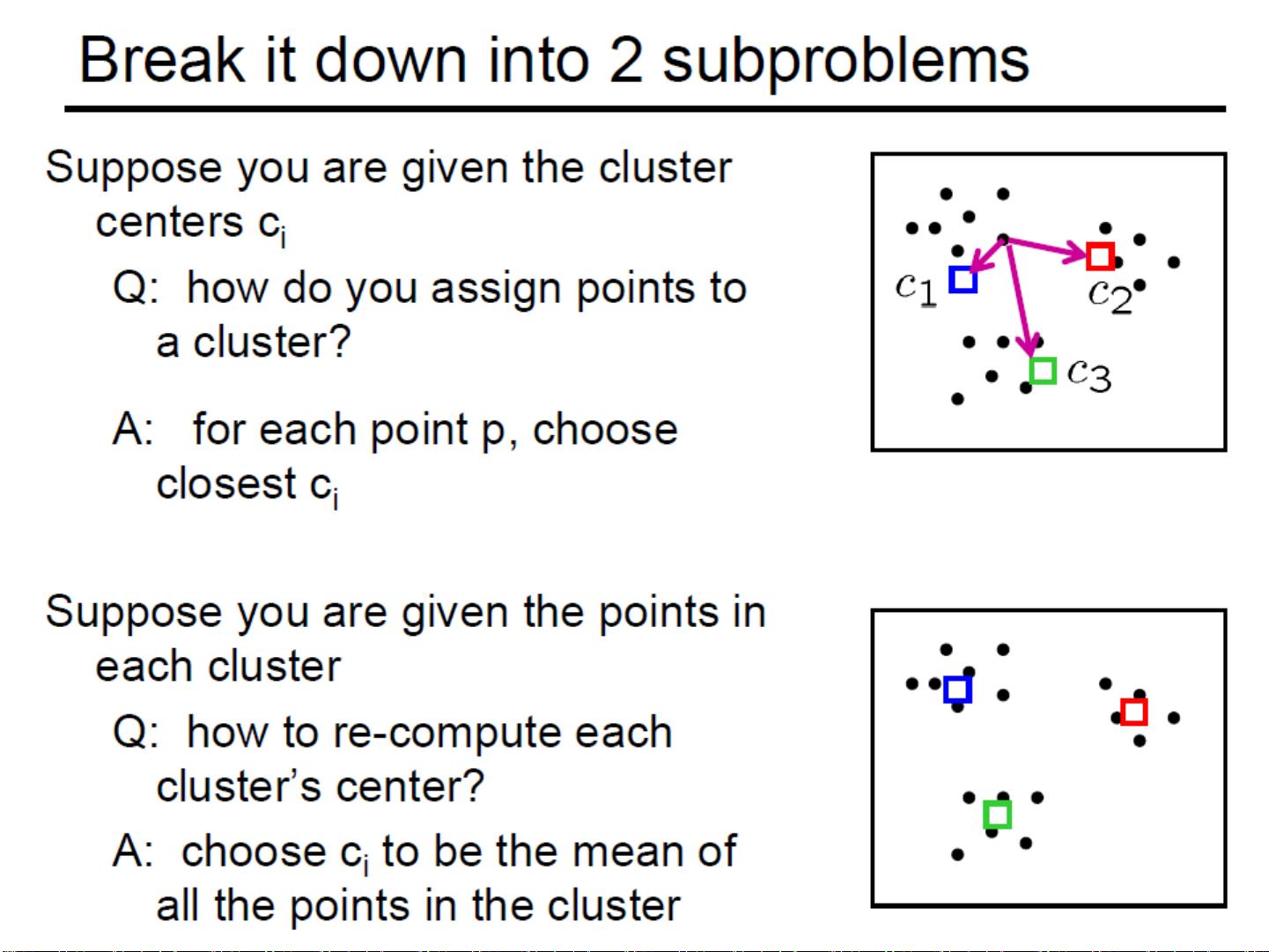
图像处理矩阵基础是数字信号处理（DSP）领域中的核心概念，它将线性代数的基本原理应用到图像分析和处理中。矩阵在图像处理中的作用包括但不限于图像变换、滤波、特征提取和压缩。本文将通过介绍向量范数的概念来深入理解这些操作。 首先，向量范数是数学中衡量向量大小的一个重要工具，它满足正定性、齐次性和三角不等式这三个基本性质。在图像处理中，范数被用于定义像素值的距离或者相似度，如常用的2范数（L2范数），它计算的是向量元素平方和的平方根，即||x||_2 = sqrt(sum(x_i^2))。Matlab中的norm函数提供了方便快捷的方式来计算不同类型的范数，比如norm(x, p)可以计算p范数，其中p=2时就等同于2范数。 接下来，通过一个实例展示了K-means聚类算法的应用，这是一种非监督学习方法，常用于数据集的分组或降维。在这个例子中，我们使用了随机生成的二维数据集X，并使用K-means算法将其分为两个簇。K-means基于距离准则（如城市街区距离'city'），通过迭代优化将数据点分配到离质心最近的簇，质心（centroids）则是每个簇的中心点表示。通过图形展示，我们可以直观地看到数据的分群结果和质心的位置。 矩阵在图像处理中还扮演着其他关键角色，例如在Singular Value Decomposition (SVD)中，通过分解图像矩阵为三个矩阵的乘积（UΣV^T），可以进行特征提取、压缩和去噪。SVD对于图像压缩尤其有用，因为它能够保持原始信息的主要特征，同时减少存储空间。 此外，矩阵还可以用于图像变换，如旋转、缩放、平移等操作，这些都可以通过特定的矩阵乘法来实现。例如，旋转矩阵会改变坐标系下的点的位置，而仿射变换矩阵则可以同时处理平移和缩放。 总结来说，图像处理矩阵基础是 DSP 中不可或缺的一部分，它涉及到向量范数的概念、矩阵运算（如SVD）、聚类算法（如K-means）以及各种图像变换技术。理解和掌握这些基础知识，有助于我们更有效地处理和分析图像数据，提升图像处理算法的精度和效率。