线性代数映射视角解析：矩阵在机器学习中的作用

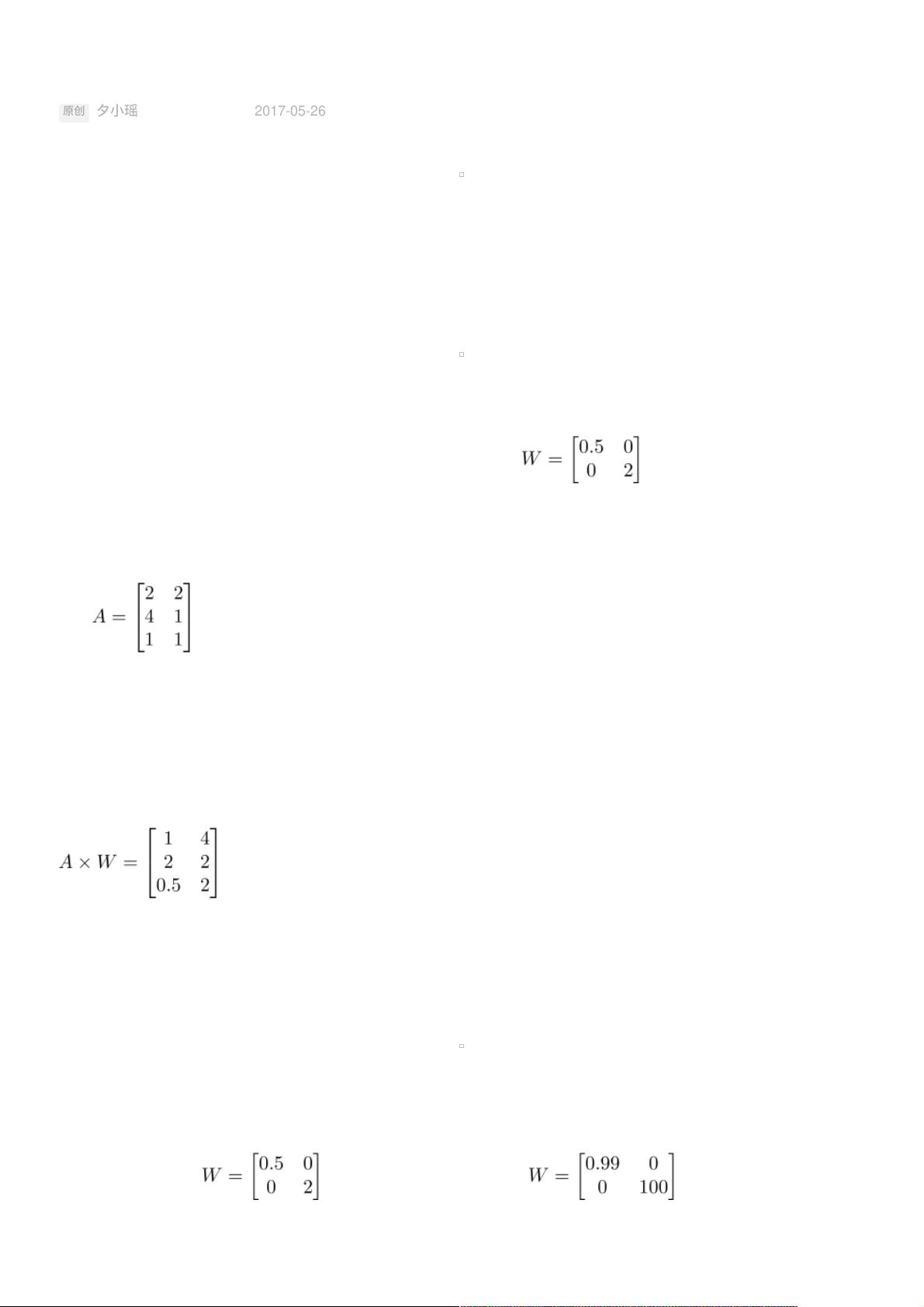
"线性代数在机器学习和神经网络中的应用" 线性代数是现代数学和计算机科学，特别是机器学习和深度学习领域的基础。它提供了处理和理解高维数据的有效工具。这篇文档《线性代数应该这样讲（二）》继续探讨了线性代数中的核心概念——矩阵，并从映射的角度进行深入解析。 首先，矩阵不仅是一种数据结构，用于存储和操作数据，同时也可以被理解为一种线性变换，即线性方程组的抽象表示。矩阵的乘法对应于这些线性变换的组合，反映了数据在不同空间之间的转换。在机器学习中，这种转换特别重要，因为它们可以帮助我们找到数据的隐藏结构或进行特征提取。 文档提到了矩阵可以被视为张量的一个切片，这是在多维数据处理中的通用概念。张量在深度学习中广泛使用，如神经网络的权重和激活。矩阵作为张量的一部分，可以表示网络中的一层，其中每一行或列对应于特定层的神经元。 作者以一个具体的例子说明矩阵作为映射的性质。假设有一个矩阵A，它描述了一个映射，将输入空间的第一个维度缩短为原来的一半，第二个维度拉伸为原来的两倍。如果我们将二维空间中的三个样本点表示为矩阵，那么通过矩阵A作用于这些样本，就能得到新的坐标，直观地体现了映射的效果。 接着，文章引入了一个更复杂的映射，该映射几乎不改变第一维度，而极大地扩展了第二维度。这可以通过一个特定的矩阵W来表示。在这种映射下，对于单位向量(1,0)（代表x轴）和(0,1)（代表y轴），映射后它们的长度和方向会发生相应的变化。这样的变换在神经网络中尤为关键，因为每一层的输出会通过权重矩阵转化为下一层的输入，这个过程就是矩阵映射的直观应用。 作者鼓励读者从不同角度理解矩阵，不应局限于单一的视角，因为矩阵在不同场景下可以有不同的含义。在神经网络中，矩阵的乘法（即权重矩阵）决定了神经元如何响应输入信号，以及如何将信息传递到下一层。激活函数的引入则进一步增加了非线性，使得网络能够学习更复杂的模式。 线性代数的矩阵理论是理解机器学习，尤其是神经网络的基础。矩阵的映射特性使我们能够描述数据的变换，这对于理解和优化模型性能至关重要。通过矩阵的运算，我们可以构建出复杂的模型，解决实际问题，比如图像识别、自然语言处理等。因此，对线性代数的深入理解是每一位从事相关领域工作的专业人士必须具备的技能。