确定有限自动机与非确定有限自动机详解

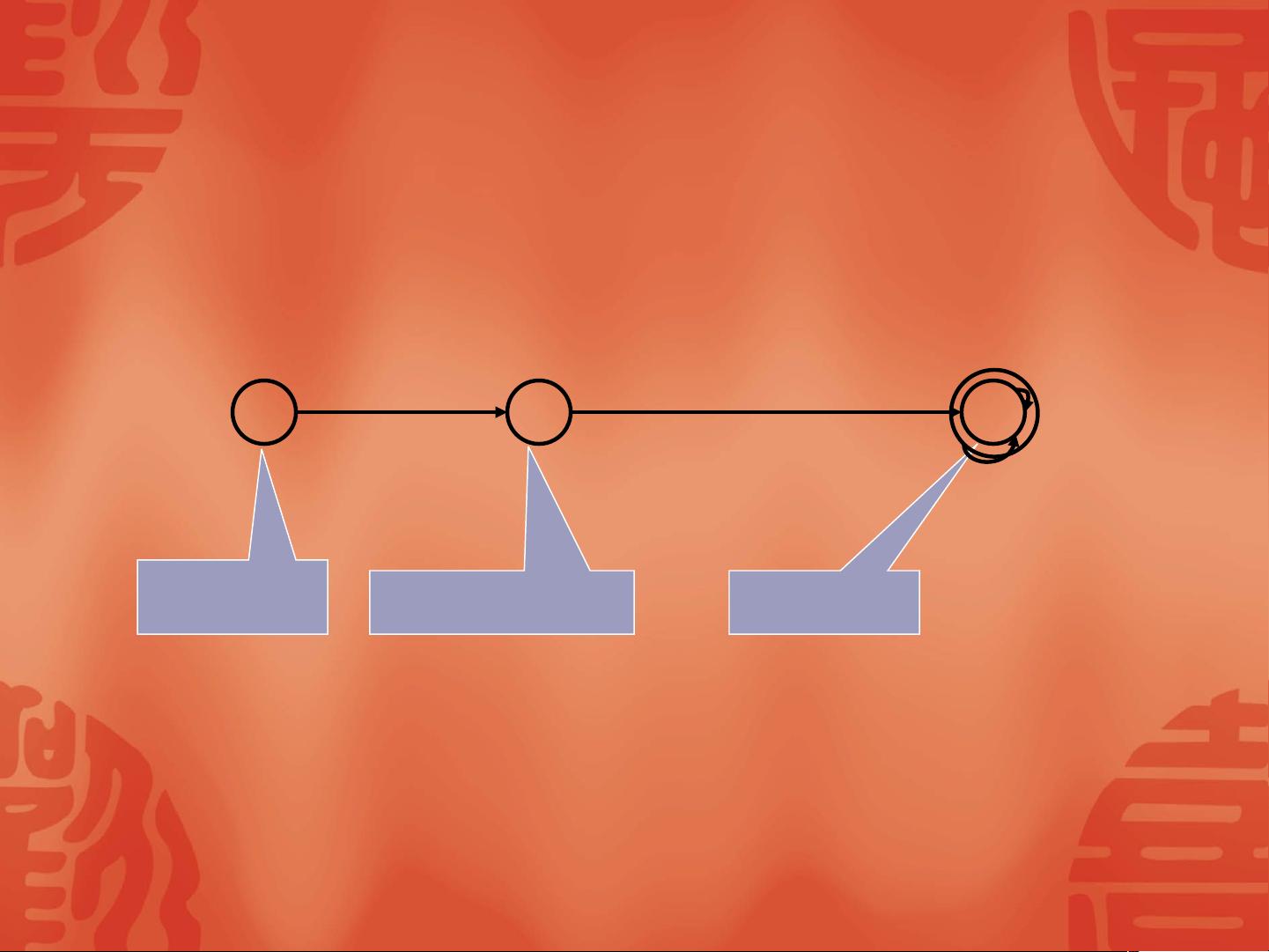
"自动机理论是计算理论的基础部分，主要研究如何用数学模型处理符号序列。确定有限自动机（DFA）和非确定有限自动机（NFA）是两种重要的自动机模型，它们在形式语言和编译原理等领域有着广泛应用。 一、转换图 转换图是一种基于字母表的有向图，它具有一个初始结点、若干个终止结点，并且每条边都带有字母表中的符号串，包括空串。转换图通过路径来接收或识别特定的符号串，路径是从初始结点到终止结点的序列。 二、确定有限自动机（DFA） DFA是一种有限状态的机器，由有限的控制器和字符输入带组成。在DFA中，每次读取一个字符时，状态会唯一地转变为另一个状态，即不存在多个后继状态。DFA的状态转换图清晰地描述了其工作流程。DFA由五元组AD=(S,,,K,F)定义，其中S是状态集合，是输入字母表，是状态转换函数，K是初始状态，F是终止状态集合。例如，一个简单的DFA可能有四个状态S0、S1、S2和S3，输入字母表包含a、b、c，初始状态是S0，终止状态是S2和S3，且有特定的转换规则。 三、非确定有限自动机（NFA） 与DFA不同，NFA允许在读取一个字符后有多个后继状态，这称为非确定性。NFA同样由五元组表示，但状态转换函数不再必须是单值映射，它可以将一个状态映射到状态集合。尽管NFA在理论上比DFA强大，因为它们能识别更多的语言，但在实际应用中，DFA往往更受欢迎，因为它们更容易实现和理解。 四、NFA与DFA的变换 可以通过构造算法将NFA转化为等价的DFA，这个过程通常涉及状态合并和消除ε-转移。ε-转移是在不读取任何输入符号的情况下就能发生状态变化的特殊转移。 五、ε-自动机 ε-自动机是指允许ε-转移的自动机，即在没有读取输入符号的情况下也能从一个状态转移到另一个状态。ε-转移使得NFA可以同时探索多个状态分支，增加了其灵活性。 六、语法图与自动机 语法图通常用于描述上下文无关文法，而自动机则是识别这些文法生成的语言的工具。通过将文法规则映射到自动机的状态转换，可以建立文法和自动机之间的联系，从而进行语言的识别。 总结来说，确定有限自动机和非确定有限自动机是计算模型中的基础概念，它们帮助我们理解和处理形式语言。DFA因其确定性和简单性在实际应用中占主导地位，而NFA则在理论上提供了更大的表达能力。通过各种转换和构造方法，两者之间可以相互转换，以适应不同的计算问题需求。"