从贝塞尔曲线到B样条曲面：图形学中的曲线构造原理

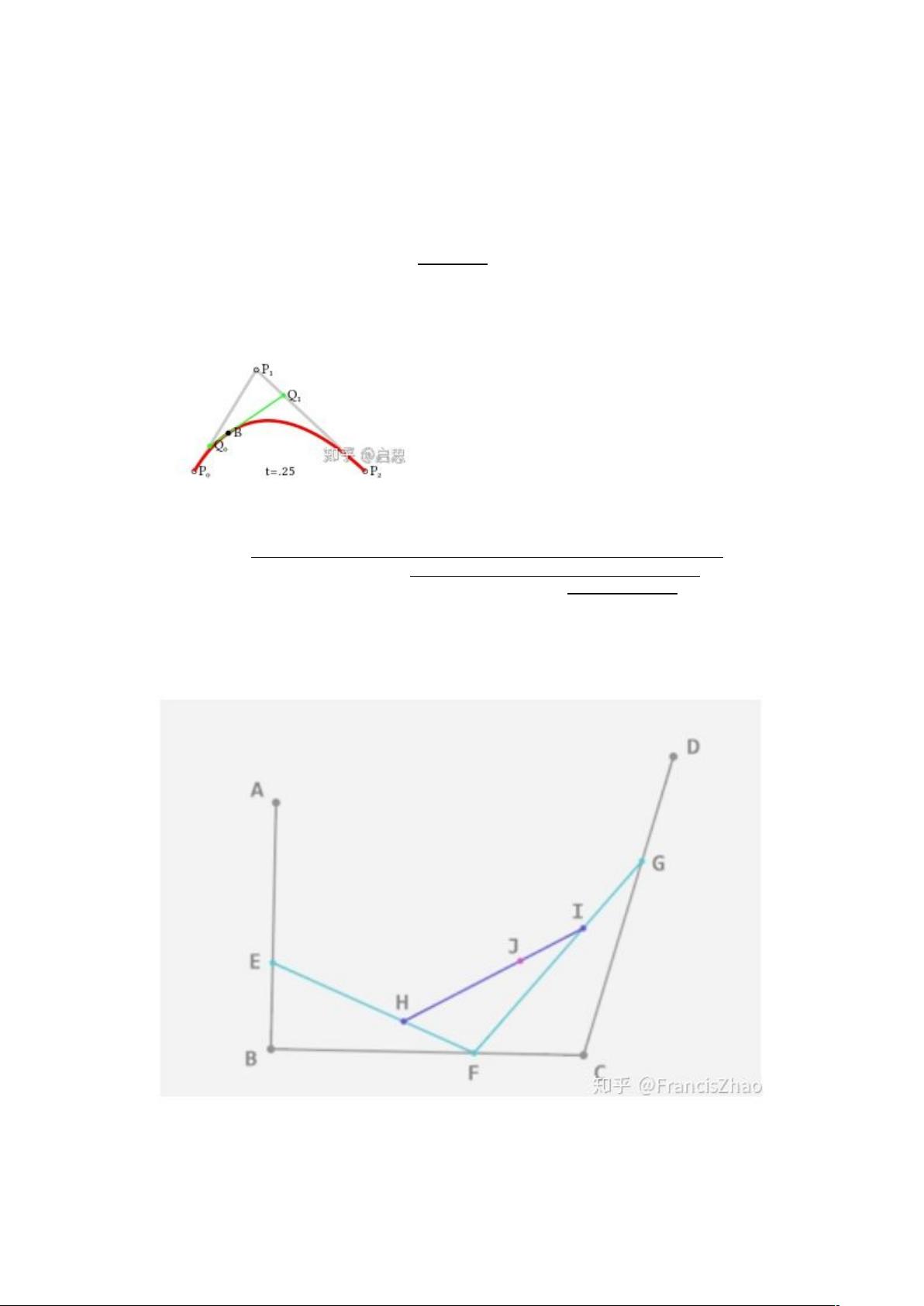
本文主要介绍了二次B样条曲面的概念，包括贝塞尔曲线的基础知识、B样条曲线的改进以及B样条曲面的构建原理。 贝塞尔曲线是图形学中广泛使用的数学工具，由法国工程师皮埃尔-贝塞尔在1962年提出。这种曲线通过一组控制点来定义，每个控制点对曲线上每一点的形状都有贡献。以二阶贝塞尔曲线为例，它由三个控制点决定，通过参数u在[0,1]区间内的变化，生成一系列点B，连成的轨迹即为贝塞尔曲线。同样的逻辑适用于更高阶的贝塞尔曲线，如三阶贝塞尔曲线，只是涉及的控制点更多，形状更复杂。 然而，贝塞尔曲线存在一些局限性，比如计算量随着控制点数的增加而增大，稳定性下降，控制点对曲线形状的影响也变得不那么明显。此外，修改一个控制点会影响到整条曲线的形状，而非局部区域。 为了解决这些问题，1972年，Gordon引入了B样条（B-Spline）概念，它基于B样条基函数，类似于分段函数，将曲线分割成多个短段，每一段可以独立控制，从而增强了局部控制能力和计算效率。B样条曲线的表达式更为复杂，涉及到(m+n+1)个控制点，以及不同的参数和指数。例如，一次均匀B样条曲线、二次均匀B样条曲线和三次均匀B样条曲线分别对应不同数量的控制点和参数范围。 B样条曲面则由B样条曲线进一步扩展，通过多个控制点构成的曲线交织在一起，形成一个连续的曲面。这个过程类似于用直线构建平面，首先创建出一系列的B样条曲线，然后将这些曲线的特定点作为新曲线的控制点，再构建新的B样条曲线，最终组合成一个B样条曲面。这个曲面的形状和特性同样受其控制点的布局和参数u、w的影响。 二次B样条曲面是基于B样条曲线理论的一种曲面表示方法，它克服了贝塞尔曲线的一些缺点，提供了更灵活的形状控制和更高的计算效率，广泛应用于计算机图形学、CAD设计和工业造型等领域。理解并掌握B样条曲面的构建原理和性质，对于进行三维建模和动画制作至关重要。