图论与网络模型：最短路径、最小生成树与最大流问题解析

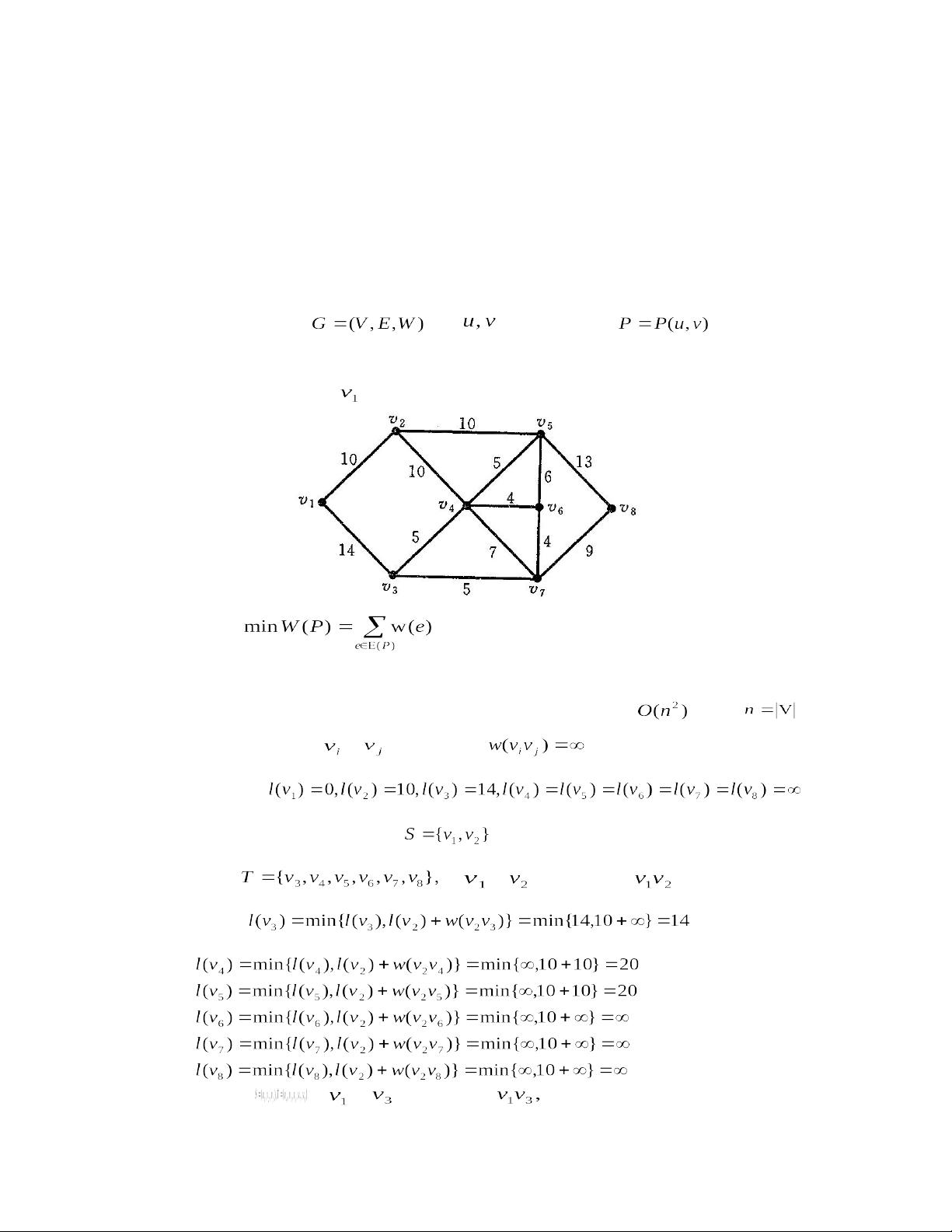
"图论与网络模型讲义涵盖了最短路径问题、最小生成树问题、网络最大流问题以及图的独立集、覆盖集与支配集问题。" 在图论与网络模型中，最短路径问题是一个核心议题。它涉及到在加权图中找到两个指定顶点之间的路径，使得路径上所有边的权重之和最小。例如，求解从一个顶点到其他所有顶点的最短路径。Dijkstra算法是解决此类问题的经典方法，其计算复杂性为O(E log V)，其中E是边的数量，V是顶点的数量。在具体应用中，最短路径问题可以用于确定最可靠路径、工序的关键路径分析，选址问题以及点带权的最短路径计算。 最小生成树问题则是在加权连通图中寻找一个生成树，使得生成树的边权重和最小。解决这个问题的算法有Kruskal和Prim两种，它们都具有O(E log V)的计算复杂性。最小生成树在实际中常用于网络设计、运输问题以及成本优化等场景。 网络最大流问题关注的是在一个有容量限制的网络中，从单一源点到单一汇点的最大流量。Ford-Fulkerson算法和Edmonds-Karp算法是解决此问题的常见方法，后者的时间复杂度为O(VE^2)，其中V是顶点数，E是边数。此外，单纯形法虽不是多项式时间算法，但在特定软件支持下也可用于求解。最大流问题广泛应用于物流网络设计、电路设计和资源分配等领域。 图的独立集、覆盖集和支配集问题是图论中的另一类问题。独立集是指图中没有相邻边的一组顶点，覆盖集则是图中每条边至少包含一个集合内的顶点，而支配集则是使得图中每个顶点都被集合内至少一个顶点直接或间接覆盖的最小顶点集合。这些问题在组合优化和图论研究中占有重要地位，如在社交网络分析、计算机科学中的数据结构优化以及资源分配问题中都有应用。 匹配问题，作为图论的一部分，关注的是找到图中最大数量的互不相交边，这在配对、调度和资源分配问题中至关重要。不同的图可能需要不同类型的匹配，如二分图的最大匹配或完全图的完美匹配。 图论与网络模型提供了强大的工具来解决各种优化问题，从寻找最经济的路径到优化网络流量，再到理解和处理复杂系统中的相互关系。这些理论和算法不仅在理论研究中有价值，也在工程、社会科学和日常生活中有着广泛的实际应用。