3D图形编程：透视投影变换详解

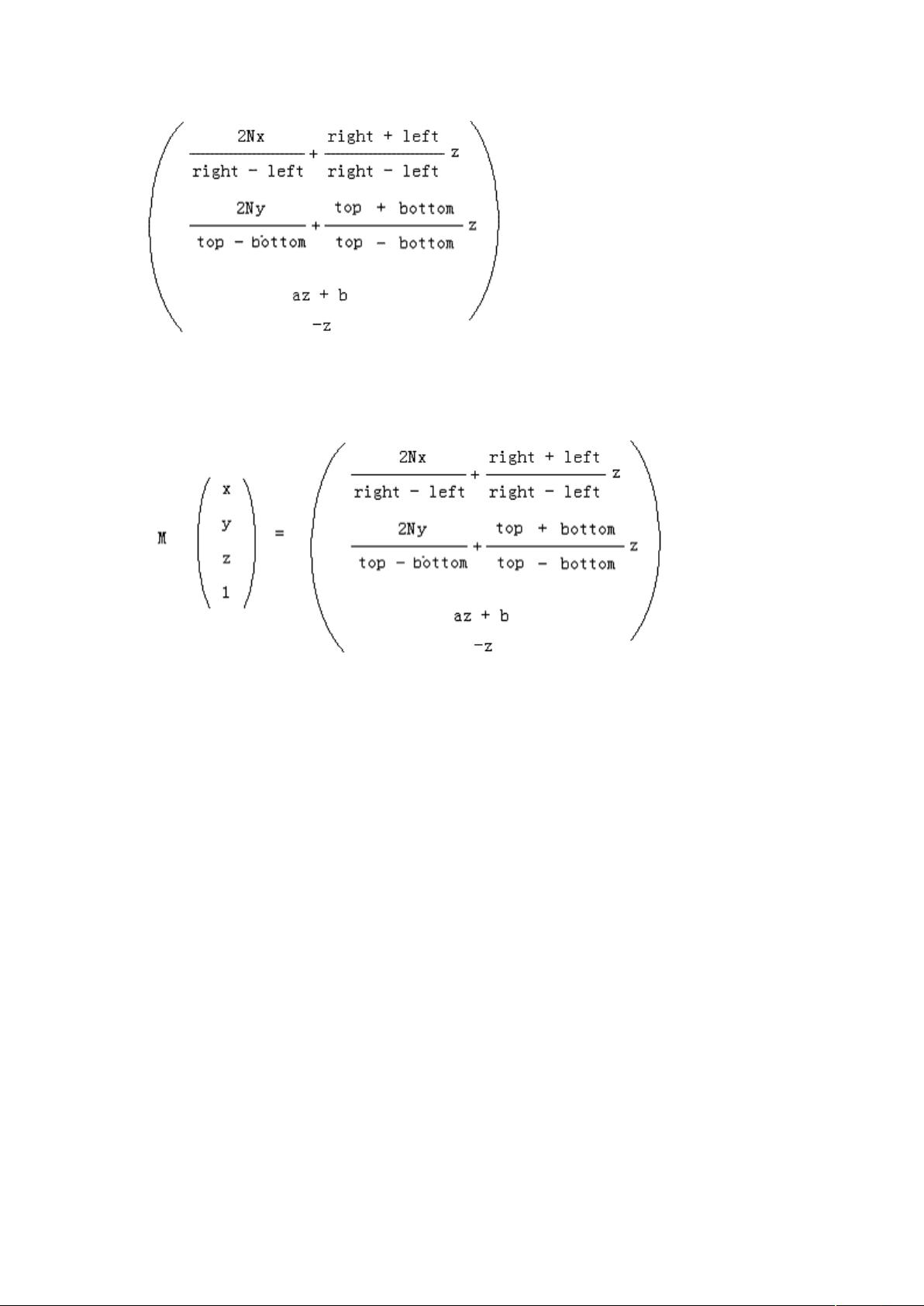
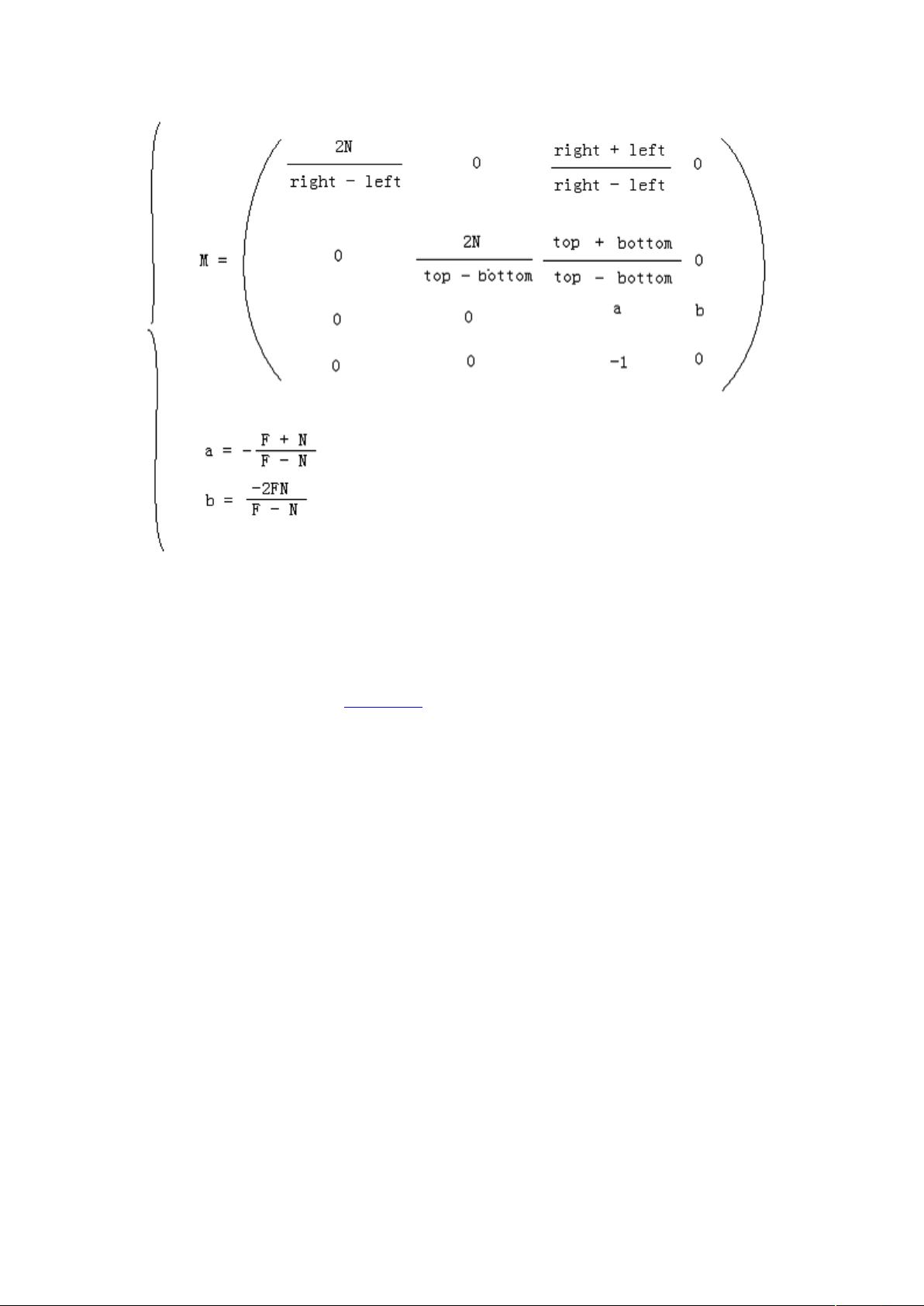
"深入探索透视投影变换，透视投影在3D图形渲染中扮演关键角色，主要涉及3D固定流水线，用于将物体从相机空间转换到观察空间。该过程包括两个主要步骤：透视矩阵乘法和透视除法。透视投影变换涉及到对齐次坐标的理解和应用，以及视锥体与规则观察体的转换。" 透视投影变换是3D图形编程中的核心概念，它在图形渲染管线中起到了将三维空间的几何形状转化为二维图像的关键作用。视锥体(frustum)是模拟真实世界中相机视野的几何结构，而规则观察体(Canonical View Volume)则是一个标准化的立方体，用于进一步处理和裁剪3D对象。 在透视投影中，每个3D点首先通过透视矩阵乘法进行转换，这个矩阵包含了视锥体的参数，如近裁剪面和远裁剪面的距离，以及视点的位置和视角。然后，经过裁剪处理后，点的坐标会通过透视除法来归一化，这一步骤确保了离相机更远的点看起来更小，从而产生深度感，形成透视效果。 理解透视投影变换离不开对齐次坐标的掌握。齐次坐标是一种扩展的坐标系统，允许在3D空间中同时表示点和向量，通常表示为四元数形式(x, y, z, w)。当w等于1时，齐次坐标表示一个普通三维点；当w不等于1时，它可以表示缩放或旋转操作。在透视变换中，w的值在透视除法中起到关键作用，确保了正确地缩放点的坐标以实现透视效果。 为了进行透视除法，点的坐标(x, y, z, w)会被除以w，得到规范化坐标(x/w, y/w, z/w)。由于视锥体内的点满足w>0，这个除法不会引入问题，并且可以消除z轴上的深度信息，便于后续的深度测试和混合操作。 在实际应用中，如OpenGL和Direct3D等API中，开发者通常不需要直接处理这些数学细节，因为库函数如gluPerspective或D3DXMatrixPerspectiveFovLH会自动创建透视投影矩阵。然而，理解这些底层原理对于优化性能、解决图形问题和设计自定义渲染算法至关重要。 透视投影变换是3D图形编程中的基础，它的理解需要对齐次坐标、视锥体、规则观察体以及矩阵运算有深入的了解。掌握这些概念不仅有助于实现复杂的3D效果，也能为成为专业图形程序员或游戏开发者打下坚实的基础。